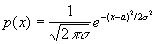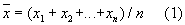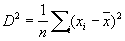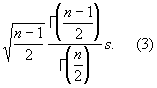что такое несмещенные оценки
Несмещённая оценка
Несмещённая оце́нка в математической статистике — это точечная оценка, математическое ожидание которой равно оцениваемому параметру.
Определение
Пусть 
— выборка из распределения, зависящего от параметра 
. Тогда оценка 
называется несмещённой, если
.
В противном случае оценка называется смещённой, и случайная величина 
называется её смеще́нием.
Примеры
— исправленная выборочная дисперсия.
Тогда 
является смещённой, а 
несмещённой оценками параметра 
. Смещенность можно доказать следующим образом:
Где 
и 
— среднее и его оценка соответственно.
Литература и некоторые ссылки
Полезное
Смотреть что такое «Несмещённая оценка» в других словарях:
Несмещённая оценка — оценка параметра Распределения вероятностей по наблюдённым значениям, лишённая систематической ошибки. Более точно: если оцениваемое распределение зависит от параметров θ1, θ2. θs, то функция θi* (x1, x2. xn) от результатов… … Большая советская энциклопедия
Состоятельная оценка — статистическая оценка параметра Распределения вероятностей, обладающая тем свойством, что при увеличении числа наблюдений вероятность отклонений оценки от оцениваемого параметра на величину, превосходящую некоторое заданное число,… … Большая советская энциклопедия
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — один из осн. разделов матем. статистики … Физическая энциклопедия
Метод наименьших квадратов — Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения. Запрос «МНК» перенаправляетс … Википедия
Статистические оценки — функции от результатов наблюдений, употребляемые для статистического оценивания (См. Статистическое оценивание) неизвестных параметров распределения вероятностей изучаемых случайных величин. Например, если X1. Xn независимые случайные … Большая советская энциклопедия
Неравенство Крамера — Рао — В математической статистике неравенством Крамера Рао (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая… … Википедия
Неравенство Крамера — В математической статистике неравенством Крамера Рао (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая… … Википедия
Статистика (функция выборки) — У этого термина существуют и другие значения, см. Статистика (значения). Статистика (в узком смысле) это измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения. В широком смысле термин (математическая)… … Википедия
Несмещенная оценка
Несмещённая оце́нка в математической статистике — это точечная оценка, математическое ожидание которой равно оцениваемому параметру.
Определение
Пусть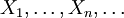 
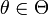
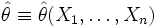
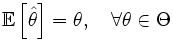
— выборка из распределения, зависящего от параметра 
. Тогда оценка 
называется несмещённой, если
.
В противном случае оценка называется смещённой, и случайная величина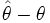 
называется её смеще́нием.
Примеры
— исправленная выборочная дисперсия.
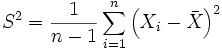
Литература и некоторые ссылки
Полезное
Смотреть что такое «Несмещенная оценка» в других словарях:
Несмещенная оценка — (unbiased estimator) статистическая точечная оценка, математическое ожидание которой совпадает с оцениваемой величиной (у нее нет систематической ошибки) … Экономико-математический словарь
несмещенная оценка — статистическая точечная оценка, математическое ожидание которой совпадает с оцениваемой величиной (у нее нет систематической ошибки). [http://slovar lopatnikov.ru/] Тематики экономика EN unbiased estimator … Справочник технического переводчика
НЕСМЕЩЕННАЯ ОЦЕНКА — (unbiased estimator) Статистический показатель, не слишком отличающийся от среднего значения. Метод оценки не всегда дает показатели, соответствующие реальности, но отклонения в любую сторону равновероятны. Экономика. Толковый словарь. М.: ИНФРА… … Экономический словарь
несмещенная оценка — 2.55. несмещенная оценка Оценка со смещением, равным нулю Источник: ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения … Словарь-справочник терминов нормативно-технической документации
несмещенная оценка — nepaslinktasis įvertis statusas T sritis Standartizacija ir metrologija apibrėžtis Įvertis, kurio poslinkis lygus nuliui. atitikmenys: angl. unbiased estimator rus. несмещенная оценка, f pranc. estimateur sans biais, m … Penkiakalbis aiškinamasis metrologijos terminų žodynas
несмещенная оценка — Оценка параметра называется несмещенной, если ее ожидаемое значение (математическое ожидание) равняется истинному значению параметра. В противном случае оценка является смещенной … Словарь социологической статистики
ОЦЕНКА СТАТИСТИЧЕСКАЯ — функция от случайных величин, применяемая для оценки неизвестных параметров теоретич. распределения вероятностей. Методы теории О. с. служат основой современной теории ошибок; обычно в качестве неизвестных параметров выступают измеряемые физич.… … Математическая энциклопедия
ОЦЕНКА НАИЛУЧШАЯ ЛИНЕЙНАЯ НЕСМЕЩЕННАЯ — (Best linear unbiased estimation). Результат решения смешанной модели, относящейся к фиксированным факторам. Процедура наилучшей линейной несмещенной оценки используется в случаях, когда требуется оценить (а не спрогнозировать) влияние каких либо … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных
Статистическое оценивание
Материал из MachineLearning.
Содержание
Постановка задачи
Различают два основных типа оценок: точечные оценки и доверительные интервалы.
Точечное оценивание
К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.
Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.
Состоятельность
Когда употребляют просто термин состоятельность, то обычно имеется в виду слабая состоятельность, т.е. сходимость по вероятности.
Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко.
Несмещенность и асимптотическая несмещенность
Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:
Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:
Сравнение оценок и эффективность
Для сравнения между собой различных оценок одного и того же параметра применяют следующий метод: выбирают некоторую функцию риска, которая измеряет отклонение оценки от истинного значения параметра, и лучшей считают ту, для которой эта функция принимает меньшее значение.
Чаще всего в качестве функции риска рассматривают математическое ожидание квадрата отклонения оценки от истинного значения
Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.
(Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.
Достаточные статистики
(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.
Доверительные интервалы
Другим типом оценок статистических параметров являются доверительные интервалы.
Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.
Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.
Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.
Несмещённая оценка
Полезное
Смотреть что такое «Несмещённая оценка» в других словарях:
Состоятельная оценка — статистическая оценка параметра Распределения вероятностей, обладающая тем свойством, что при увеличении числа наблюдений вероятность отклонений оценки от оцениваемого параметра на величину, превосходящую некоторое заданное число,… … Большая советская энциклопедия
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — один из осн. разделов матем. статистики … Физическая энциклопедия
Метод наименьших квадратов — Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения. Запрос «МНК» перенаправляетс … Википедия
Статистические оценки — функции от результатов наблюдений, употребляемые для статистического оценивания (См. Статистическое оценивание) неизвестных параметров распределения вероятностей изучаемых случайных величин. Например, если X1. Xn независимые случайные … Большая советская энциклопедия
Неравенство Крамера — Рао — В математической статистике неравенством Крамера Рао (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая… … Википедия
Неравенство Крамера — В математической статистике неравенством Крамера Рао (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая… … Википедия
Статистика (функция выборки) — У этого термина существуют и другие значения, см. Статистика (значения). Статистика (в узком смысле) это измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения. В широком смысле термин (математическая)… … Википедия
Статистическое оценивание
Материал из MachineLearning.
Содержание
Постановка задачи
Различают два основных типа оценок: точечные оценки и доверительные интервалы.
Точечное оценивание
К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.
Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.
Состоятельность
Когда употребляют просто термин состоятельность, то обычно имеется в виду слабая состоятельность, т.е. сходимость по вероятности.
Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко.
Несмещенность и асимптотическая несмещенность
Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:
Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:
Сравнение оценок и эффективность
Для сравнения между собой различных оценок одного и того же параметра применяют следующий метод: выбирают некоторую функцию риска, которая измеряет отклонение оценки от истинного значения параметра, и лучшей считают ту, для которой эта функция принимает меньшее значение.
Чаще всего в качестве функции риска рассматривают математическое ожидание квадрата отклонения оценки от истинного значения
Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.
(Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.
Достаточные статистики
(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.
Доверительные интервалы
Другим типом оценок статистических параметров являются доверительные интервалы.
Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.
Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.
Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.