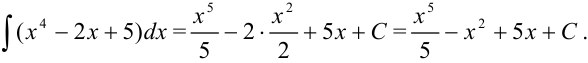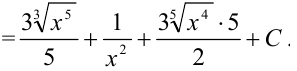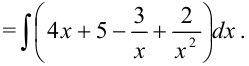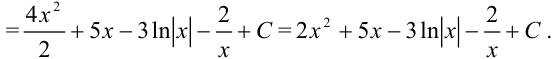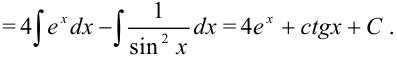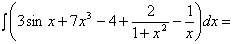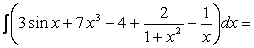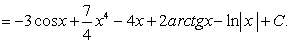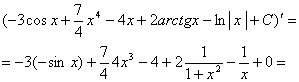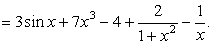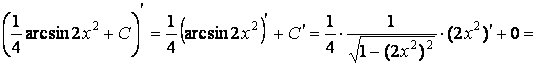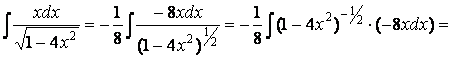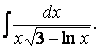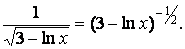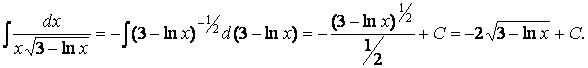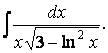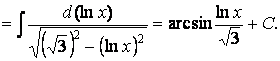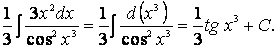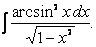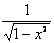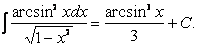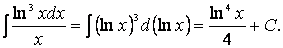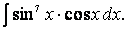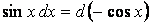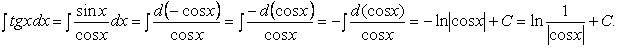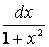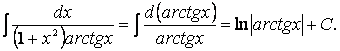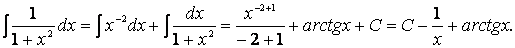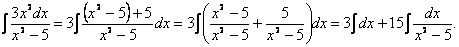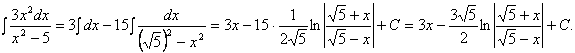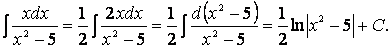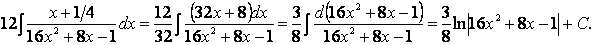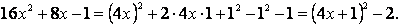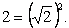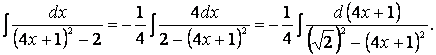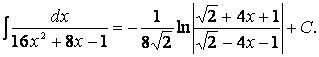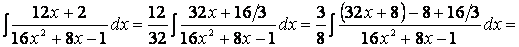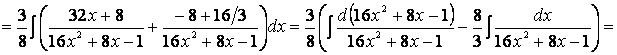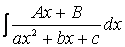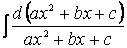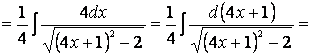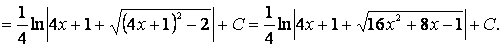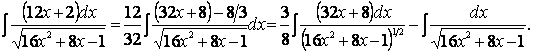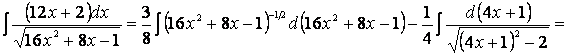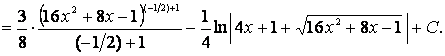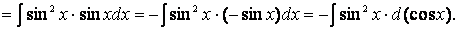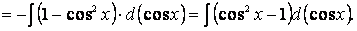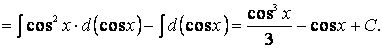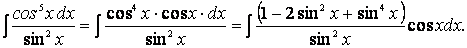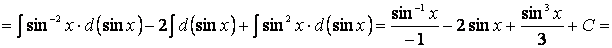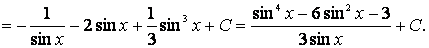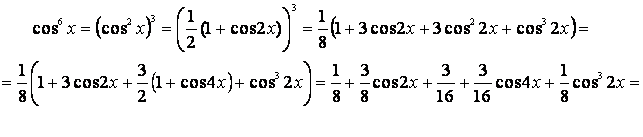что такое непосредственное интегрирование

Непосредственное интегрирование

Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Пример №19.1.

Найдите .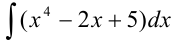

Решение:

Воспользуемся свойствами неопределенного интеграла: представим интеграл как сумму и разность соответствующих интегралов:

. Вынесем константы за знак интеграла:

и воспользуемся табличными интегралами. Получим, что

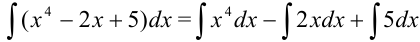
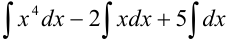
Пример №19.2.

Найдите .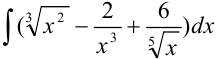

Решение:

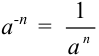
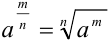
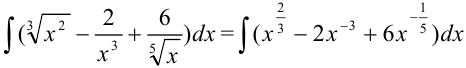
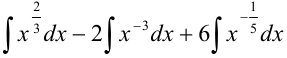
Каждое слагаемое, стоящее под знаком интеграла, представим в виде степени с рациональным показателем. Для этого применим следующие свойства степени: ; . Тогда . Представим данный интеграл как сумму и разность интегралов, вынесем константы за знак интеграла:

. Воспользовавшись табличным
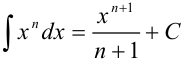
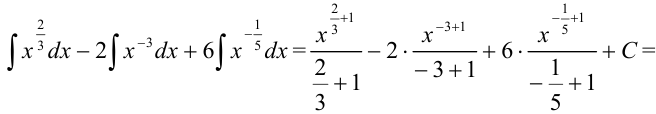
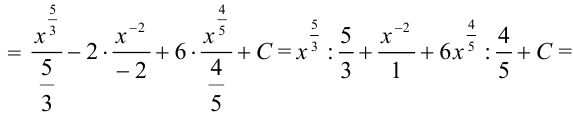
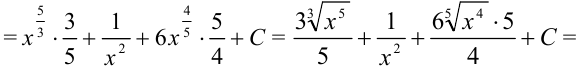
интегралом , получим:

Пример №19.3.

Найдите .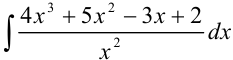

Решение:

Разделив почленно числитель на знаменатель, получим

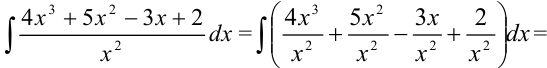
Представим данный интеграл как сумму и разность интегралов, вынесем константы за скобки:

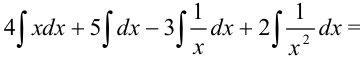
Пример №19.4.

Найти .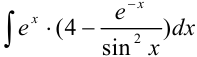

Решение:

Раскрывая скобки и применяя табличные интегралы, получим:

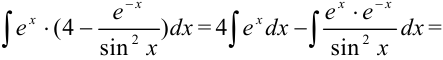
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Что такое непосредственное интегрирование

Вычисление неопределенных интегралов с помощью таблицы интегралов и их основных свойств называется непосредственным интегрированием.

Пример 1. Найдем интеграл

Применив второе и пятое свойства неопределенного интеграла, получим

Далее, используя формулы II , Ш, IV , VIII таблицы и третье свойство интегралов, находим каждый из слагаемых интегралов отдельно:

Проверим результат дифференцированием. Найдем производную полученного выражения:

Мы получили подынтегральную функцию, это доказывает, что ин­тегрирование выполнено верно.

В таблице интегралов приведено следствие III а из формулы III :

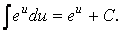
Чтобы воспользоваться этим следствием, найдем дифференциал функции, стоящей в показателе степени:

Для создания этого дифференциала достаточно домножить знаменатель дроби под интегралом на число 2 (очевидно, чтобы дробь не изменилась, необходимо при этом умножить на 2 и числитель). После вынесения постоянного множителя за знак интеграла он становится готовым для применения табличной формулы III а :

следовательно, интегрирование выполнено правильно.

Так как из выражения, стоящего в числителе, можно сконструировать дифференциал квадратичной функции, то следует выделить в знаменателе такую функцию:

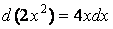
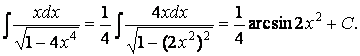
Для создания ее дифференциала достаточно умножить числитель на 4 (знаменатель при этом также умножим на 4 и вынесем этот множитель знаменателя за интеграл). В результате мы получим возможность использовать табличную формулу X :

т.е. интегрирование выполнено верно.

Заметим, что теперь квадратичная функция, дифференциал которой 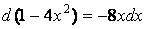можно создать в числителе, является подкоренным вы­ражением. Поэтому разумно будет записать подынтегральную функцию как степенную, чтобы воспользоваться формулой I таблицы интегралов:

Вывод: интеграл найден правильно.

Обратим внимание на то, что подынтегральное выражение содержит

Поэтому разумно представить дробь в виде степени:

Тогда после домножения числителя и знаменателя на (-1) мы получим степенной интеграл (табличная формула I ):

Дифференцированием результата убеждаемся, что интегрирование выполнено верно.

Легко убедиться, что в этом интеграле из выражения 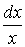дифференциал подкоренной функции не удастся получить с помощью числовых коэффициентов. Действительно,

где k —константа. Зато, по опыту примера 3, можно сконструировать интеграл, совпадающий по виду с формулой X из таблицы интегралов:

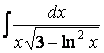
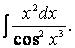
Обратим внимание на то, что в числителе легко создается дифференциал кубической функции d ( x 3 ) = 3 x 2 dx . После чего мы получаем возможность использовать табличную формулу VI :

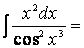
Известно, что производной функции arcsin x является дробь

воспользуемся той же табличной формулой I и тем, что

Пример 11. Для нахождения интеграла

воспользуемся последовательно: тригонометрической формулой

и формулой II таблицы интегралов:

Заметим, что степень переменной в числителе на единицу меньше, чем в знаменателе. Это позволяет в числителе создать дифференциал знаменателя. Найдем

.

После вынесения постоянного множителя за знак интеграла домножим числитель и знаменатель подынтегральной дроби на (-7), получим:

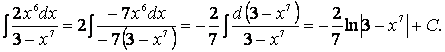
(Здесь использовалась та же формула II из таблицы интегралов).

Пример 14. Найдем интеграл

.

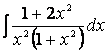
Представим числитель в ином виде: 1 + 2х 2 = (1 + х 2 ) + х 2 и выпол­ним почленное деление, после чего используем пятое свойство интегра­лов и формулы I и VIII таблицы:

Вынесем постоянный множитель за знак интеграла, вычтем и приба­вим в числителе 5, затем выполним почленное деление числителя на знаменатель и воспользуемся пятым свойством интеграла:

Для вычисления первого интеграла используем третье свойство ин­тегралов, а второй интеграл представим в виде, удобном для применения формулы IX :

Отметим, что показатель степени переменной в числителе на едини­цу меньше, чем в знаменателе (что характерно для производной), а зна­чит, в числителе можно сконструировать дифференциал знаменателя. Найдем дифференциал выражения, стоящего в знаменателе:

Здесь мы использовали II табличный интеграл.

Рассмотрим подобную же ситуацию в следующем примере.

.

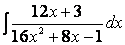
Вычислим дифференциал знаменателя:

.

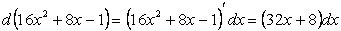
Создадим его в числителе с помощью четвертого свойства интегралов:

=

=

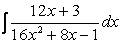
Более сложная подобная ситуация будет рассмотрена в примере 19.

Выделим в знаменателе полный квадрат:

После выделения полного квадрата в знаменателе мы получили интеграл, близкий по виду к формулам VIII и IX таблицы интегралов, но в знаменателе формулы VIII слагаемые полные квадраты имеют одинаковые знаки, а в знаменателе нашего интеграла знаки слагаемых различны, хотя и не совпадают со знаками девятой формулы. Добиться полного совпадения знаков слагаемых в знаменателе со знаками в формуле IX удается вынесением коэффициента (-1) за интеграл. Итак, чтобы применить формулу IX таблицы интегралов, проведем следующие мероприятия:

1) вынесем (-1) за скобки в знаменателе и затем за интеграл;

2) найдем дифференциал выражения

;

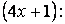
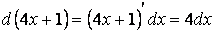
3) создадим в числителе найденный дифференциал;

4) представим число 2 в виде, удобном для применения формулы IX таблицы:

Используя IX формулу таблицы интегралов, получим

Используя опыт, приобретенный при отыскании интегралов в пре­дыдущих двух примерах, и полученные в них результаты, будем иметь

Обобщим некоторый опыт, полученный в результате решения примеров 17,18,19.

Итак, если мы имеем интеграл вида

( пример 19 ) после создания в числителе производной знаменателя распадается на два интеграла: первый – вида

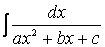
Подкоренное выражение имеет вид выражения

Для применения формулы XI в числителе должен стоять дифференциал

;

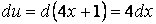
поэтому следует создать его, домножив числитель и знаменатель дроби на число 4:

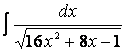
Пример 21. Найдем теперь

Используя опыт предыдущих примеров, создадим в числителе дифференциал знаменателя и разобьем интеграл на два, вынеся ненужные числовые коэффициенты за интегралы:

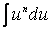
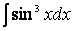
Первый интеграл перепишем в виде степенного (т.е. в виде ), a второй был уже взят нами в предыдущем примере, поэтому

Теперь выразим sin 2 x через cos x и внесем знак минус в скобки:

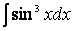
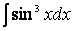
Аналогично поступают всегда при вычислении интегралов вида

,

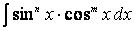
если один из показателей степени положительное нечетное число, а второй—произвольное действительное число ( пример 23).

Используя опыт предыдущего примера и тождество

cos 4 x = (cos 2 x ) 2 = (l — sin 2 x) 2 = 1— 2sin 2 x + sin 4 x,

Выполнив почленное деление слагаемых числителя на знаменатель, будем иметь

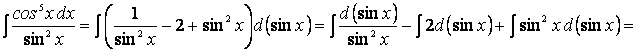
При интегрировании четных степеней тригонометрических функций сначала следует по возможности понизить степень, используя известные формулы:

.

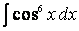
Преобразуем подынтегральную функцию:

Подставив полученную сумму под интеграл, получим

Источник

Метод непосредственного интегрирования

Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Таким образом, алгоритм действий следующий:

В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла.

При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.

Примеры решения интегралов данным методом

Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к нескольким табличным.

В некоторых случаях выражение, стоящее под знаком интеграла, можно с помощью алгебраических преобразований упростить так, чтобы можно было применить метод непосредственного интегрирования.

Метод непосредственного интегрирования не по зубам? Тебе ответит эксперт через 10 минут!

Решение. Используем формулу квадрата суммы и свойства интеграла, затем приведем данный интеграл к нескольким табличным.

$\int\left(x^<4>+\sqrt\right)^ <2>d x=\int\left(x^<8>+2 x^ <4>\cdot \sqrt+x\right) d x=$

$=\int\left(x^<8>+2 x^<4,5>+x\right) d x=\int x^ <8>d x+\int 2 x^ <4,5>d x+\int x d x=$

Решение. Упростим подынтегральную функцию, затем с помощью свойств интеграла приведем данный интеграл к нескольким табличным.

$=\int\left(x+3^-\cos x\right) d x=\int x d x+\int 3^ d x-\int \cos x d x=$

Решение. Для упрощения подынтегральной функции воспользуемся тригонометрическими функциями. Затем с помощью свойств интеграла приведем данный интеграл к табличному виду.

$\int \operatorname^ <2>x d x=\int \frac <\sin ^<2>x> <\cos ^<2>x> d x=\int \frac <1-\cos ^<2>x> <\cos ^<2>x> d x=$

Источник