что такое неполное делимое первое неполное делимое

Как найти первое неполное делимое и количество цифр в частном?

В самом начале обучения навыку деления чисел дети часто допускают ошибки. Одними из самых распространенных, помимо ошибок непосредственно в совершении промежуточных вычислений, являются появление «лишних» цифр и потеря нулей в частном. Их возникновение зачастую связано с такими причинами:

Этой статьей я хочу помочь школьникам восполнить пробелы в вышеупомянутых базовых знаниях, чтобы в дальнейшем они смогли избегать ошибок при совершении действия деления в столбик.

Как найти первое неполное делимое?

Рассмотрим подробно по шагам на таком примере \( <\color75184\div 12>\).

1. Смотрим, сколько разрядов в делимом и какая цифра стоит на позиции самого старшего разряда этого числа.

1. 1. Проверяем, можно ли это количество единиц этого разряда разделить на делитель так, чтобы получилось натуральное число?

1. 2. Если разделить нельзя, смотрим на количество единиц следующего разряда и проверяем, можем ли мы их разделить на делитель?

В числе 75184 всего 75 единиц разряда тысяч. 75 тысяч можно разделить на 12 – получится 6 полных тысяч, и 3 тысячи неразделенные.

2. Если можно разделить количество единиц разряда на делитель, то это количество единиц и будет первым неполным делимым.

В нашем примере это 75 тысяч.

Каждая оставшаяся цифра делимого будет участвовать в формировании остальных неполных частных, о чем подробно рассказано в уроке Деление натуральных чисел.

Как найти количество цифр в частном?

Так как первое неполное делимое в данном примере – это 75 тысяч, то есть, мы делим единицы тысяч, тогда самый старший разряд частного также будет тысячи. Значит, помимо цифры самого большого разряда, будут ещё три цифры: в сотнях, десятках и простых единицах.

Итак, чтобы узнать количество цифр в частном, нужно:
1. Найти первое неполное делимое.
2. Посчитать, сколько в делимом остальных цифр.
3. Прибавить к этому количеству единицу (цифра частного, полученная после деления первого неполного делимого).
4. Результат и будет количеством цифр в частном.

Поделим, и убедимся:

В конце хочу сказать, что определение количества цифр в частном помогают развить и укрепить очень необходимый для младших школьников навык – самоконтроль.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3 / 5. Количество оценок: 17

Источник

Предупреждение ошибок учащихся при делении многозначных чисел

В настоящей статье рассматриваются причины и пути предупреждения у учащихся ошибок, заключающихся в пропуске цифр частного (потеря нулей в частном) и в по лучении лишних цифр в частном.

Остановимся на каждой из указанных причин и путях их устранения.

Обычно определение количества цифр в частном проводится в результате таких рассуждений: “Первое неполное делимое 8 сотен, значит, в частном будет три цифры. ”

Однако абсолютное большинство опрошенных учащихся не смогли объяснить, почему из того, что если первое неполное делимое 8 сотен, то в частном будет три цифры. Отсутствие логического перехода от разряда первого неполного делимого к количеству цифр частного — основная причина непонимания учащимися этого шага, а потому и его невыполнения.

Подробнее объяснение определения количества цифр частного дано в пособии для учителя при выполнении деления 936 на 4: “9 сотен — это первое неполное делимое. Когда разделим сотни, то в частном получим сотни, а сотни в записи числа стоят на третьем месте, значит, в частном будет 3 цифры”.

Приведенные рассуждения конкретизируют важное общее положение: разряд первого неполного делимого является и высшим разрядом частного. Указанное общее положение необходимо довести и до учащихся. Это может быть сделано в результате обобщения способа определения количества цифр частного для конкретных случаев деления уже на уроке ознакомления с алгоритмом деления.

Ниже описан возможный вариант соответствующей части урока.

После объяснения и выполнения деления одним-двумя учащимися у доски учитель просит детей назвать первый шаг алгоритма. Они называют выделение первого неполного делимого, определение количества цифр частного. Затем детям дается задание: для каждого случая деления (785:5, 434:7, 12360:6, 1736:8) выделить первое неполное делимое и определить количество цифр частного, проведя необходимые рассуждения.

Учитель направляет ответы учащихся так, чтобы количество цифр частного определялось, в результате примерно таких рассуждений: “Первое неполное делимое в примере 785:5 будет 7 сотен, значит, первая цифра частного будет обозначать сотни. Тогда в частном будут сотни, десятки и единицы, т. е. три цифры”. “Во втором примере (434:7) первое неполное делимое 43 десятка, значит, первая цифра частного будет обозначать десятки (высший разряд частного – десятки). Значит, частное будет состоять из десятков и единиц. Частное — двузначное число”. “В третьем примере (12 360:6) первое неполное делимое 12 тысяч, значит, высший разряд частного — тысячи. Тогда частное будет состоять из тысяч, сотен, десятков и единиц, значит, в частном — четыре цифры”. “В четвертом примере (1 736:8) первое неполное делимое 17 сотен, значит, высший разряд частного — сотни. Поэтому частное будет содержать сотни, десятки и единицы, т. е. три цифры”.

При выполнении этого задания полезно на доске выделить первое неполное делимое, ниже записать название разряда этого неполного делимого и название высшего разряда частного, отметить точками количество цифр частного. Общий вывод — разряд первого неполного делимого является высшим разрядом частного — может быть сделан самим учителем. Требовать запоминания учащимися определения этого, вывода не нужно.

Далее дети продолжают выполнение тренировочных упражнений в делении на однозначное число, комментируя каждый шаг алгоритма и объясняя способ определения количества цифр частного.

В дальнейшем полезно в устные упражнения включать специальные задания на определение количества цифр частного, например, такие:

1. Сколько цифр будет содержать частное и почему, если первое неполное делимое 12 десятков? 4 сотни? 57 тысяч? 19 десятков тысяч?

2. Выполняя деление в следующих случаях:

1) 9870:35
2) 136576:64
3) 95345:485
4) 76171:19
5) 720036:36

ученик в частном получил соответственно:

1) трехзначное число; 2) четырехзначное число; 3) двухзначное число; 4) четырехзначное число; 5) трехзначное число.

В каких случаях частное найдено неверно? Почему?

3. Не выполняя действий деления и умножения, укажите, какие из равенств неверны:

116174:58=203
44172:9 =4908
21476:7 =368

Верно ли, что меньшее число не делится на большее? Верно, но лишь для деления нацело. Действительно, разделить нацело одно число на другое — это значит найти такое третье целое неотрицательное число, умножив на которое делитель получим делимое. Если делимое меньше делителя (но не равно нулю), то такого целого неотрицательного числа найти нельзя, т. е. для случая деления, например, 2:7 частного при делении нацело не существует.

Другое дело, если рассматривается деление с остатком. В этом случае разделить, например, 3 на 11 означает найти таких два целых неотрицательных числа — частное и остаток, чтобы сумма произведения частного на делитель и остатка была равна делимому. Указанному условию для чисел 3 и 11 удовлетворяют частное и остаток 3. Действительно:

0.11+3=3, т. е. 3:11=0 (ост. 3), где 3 25.01.2010

Источник

Математика. 4 класс

Конспект урока

Математика, 4 класс

Перечень вопросов, рассматриваемых в теме:

— как письменно делить трехзначные числа на однозначные?

— какой алгоритм письменного деления многозначного числа на однозначное?

Алгоритм – упорядоченный набор однозначных выполнимых шагов.

Трехзначное число – число, которое состоит из сотен, десятков и единиц первого класса.

Первое неполное делимое – это первое число, которое делится на знаменатель.

Основная и дополнительная литература по теме урока:

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с. 18, 22

3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с. 46-47

4. Волкова С. И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – с. 36-37

Теоретический материал для самостоятельного изучения:

Вы уже умеете делить числа в столбик. Рассмотрим теперь более сложный случай.

Фермер Василий собрал в своем саду 372 кг вишни. Он и его 3 сына поделили ягоды поровну между собой и отправились на рынок. Сколько килограммов вишни должен продать каждый член семьи?

Начинаем деление с сотен. Сотен 3, но 3 сотни нельзя разделить на 4 так, чтобы в частном получились сотни. Делим десятки. Три сотни и 7 десятков – это 37 десятков. Делим 37 десятков на 4. В частном будет 9. Умножаем 9 на 4, чтобы узнать сколько десятков разделили. Получается, что разделили 36 десятков. Вычитаем из тридцати семи 36, получается 1. Значит, осталось разделить еще 1 десяток.

Переходим к делению единиц. Записываем две единицы рядом с остатком от деления десятков. 1десяток и 2 единицы – это 12 единиц. Делим 12 на 4, в частном 3. Умножаем 3 на 4, получаем 12. Вычитаем 12 из двенадцати. Осталось 0. Читаем ответ: 93.

Итак, важно запомнить: деление трехзначных чисел в столбик происходит поразрядно и начинается с высшего разряда. При нахождении каждой цифры частного, надо вспомнить три операции: деление, умножение и вычитание.

Рассмотрим еще один случай деления.

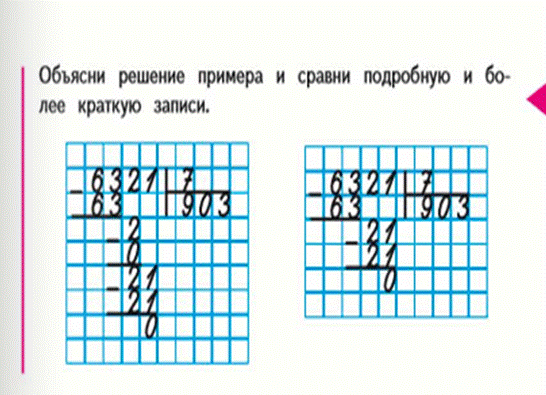
Слив фермер собрал 621 кг. Поделил их между тремя сыновьями и отправил их на рынок. Сколько килограммов слив должен продать каждый сын?

Разделим 621 на 3. Начнем деление с сотен. Делим 6 сотен на 3, в частном будет 2 сотни. Умножаем 2 на 3, чтобы узнать, сколько сотен разделили. Получается, разделили 6 сотен. Вычитаем 6 из шести, получаем 0. Значит, все сотни разделили. Ноль не пишем. Приступаем к делению десятков. Записываем 2 десятка ниже. При делении числа 2 на 3 получается 0. Умножаем 0 на 3, чтобы узнать сколько десятков разделили. Получается, что разделили 0 десятков. Вычитаем из двух ноль. Получается 2. Нам по-прежнему осталось разделить 2 десятка. Переходим к делению единиц. Записываем единицу ниже рядом с остатком 2. Два десятка и одна единица – это 21 единица. 21 делим на 3. В частном получаем 7 единиц. Умножаем 7 на 3, чтобы узнать сколько разделили единиц. Вычитаем 21 из двадцати одного, чтобы узнать остаток от деления единиц. Остаток равен 0. Читаем ответ: двести семь.

Задания тренировочного модуля:

1. Найдите значения выражения, считая устно или письменно:

Источник

выделяем первое неполное делимое (это самое малое число, начиная с высшего разряда, которое можно разделить на делитель так, чтобы получилось однозначное число не равное 0).

Определяем количество цифр в частном (для этого узнаем, из каких разрядных единиц состоит первое неполное делимое).

Подбираем первую цифру частного.

Узнаем, сколько единиц первого неполного делимого разделили (для этого делитель умножим на первую цифру частного).

Находим остаток, т.е. узнаем, сколько единиц первого неполного делимого не разделили.

Сравниваем остаток с делителем (если остаток меньше делителя, то цифру частного подобрали верно).

Определяем второе неполное делимое (оно состоит из остатка и единицы следующего разряда делимого) и т.д., начиная с пункта 3).

Деление выполняем до тех пор, пока не разделим единицы каждого разряда делимого.

Далее работа продолжается в концентре «Миллион».

Показываем, как использовать этот алгоритм при делении многозначных чисел на однозначное число.

М4М ч.1 с.81-83 и частные случаи с нулями с.85-87

М4М, ч.1 стр. 82

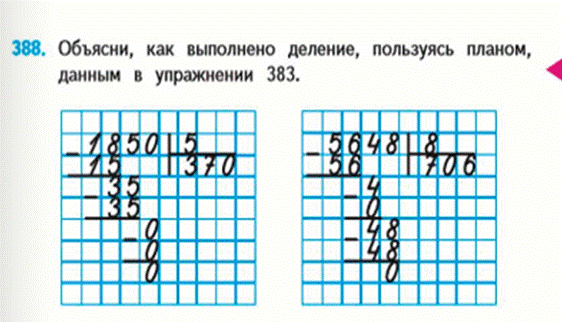
По аналогии происходит обычное деление многозначного на однозначное по первому алгоритму.

М4М, ч.1, стр. 83

Деление многозначного на однозначное, когда первое неполное делимое выражено двузначное число.

М4М,ч.1, стр. 85

1) когда на конце делимого и частного получается 0;

2) когда в середине частного получается 0.

М4М, ч.1, стр. 87

Частный случай, когда в середине частного получается 0.

Показано, как можно сократить запись при таком случае.

Рассмотрим поподробнее, как изучается прием письменного деления на однозначное число в разных учебниках математики.

Программа Н.Б. Истоминой

По программе Н.Б. Истоминой детям сначала предлагается объяснить, как выполнено деление столбиком. Затем вспоминают устный прием. Затем дается подробное объяснение приема. Также дан подробный алгоритм. Автор учебника обращает внимание детей на то, что деление в письменном приеме обозначается «уголком», а также вводится понятие «неполное делимое». Все это можно увидеть на страницах 79-83.

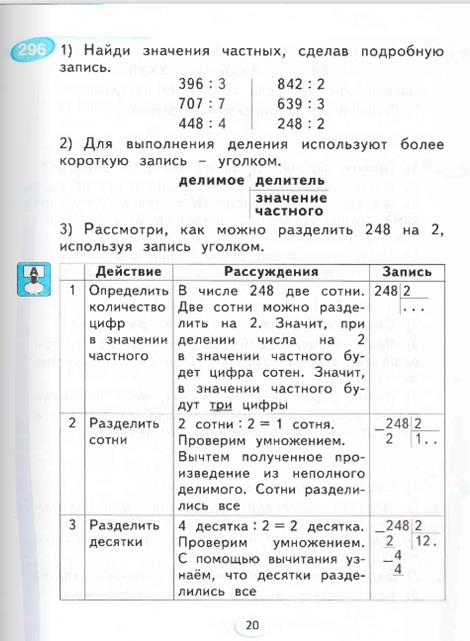
М4И, ч.1, стр. 79-83

В данном приеме можно выделить несколько частных случаев.

Случай, когда первое неполное делимое выражено двузначным числом

Оставшуюся единицу первого неполного делимого переводят в другой разряд

Случай с нулем в частном

Рассмотрим их поподробнее.

Далее в одном из упражнений вводят частный случай, когда в делимом нули на конце.

М4И,ч.1,стр.84

Алгоритма уже нет, предлагают детям объяснить самостоятельно.

Программа И.И. Аргинской

По программе И.И. Аргинской данный прием дети начинают изучать в 3 классе. Рассмотрим поподробнее.

М3А, ч.2, стр. 20-21

На этой странице вводится прием письменного деления на однозначное число. Затем дается тот же алгоритм, но оставшуюся единицу первого неполного делимого переводят в другой разряд – из сотен в десятки:

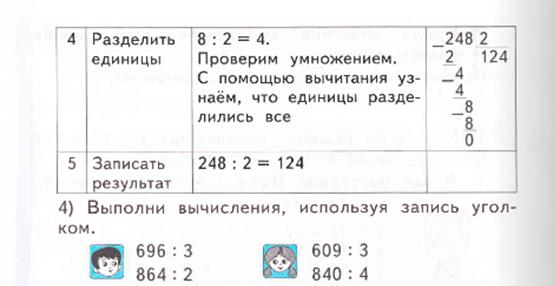
Затем дается тот же алгоритм, но оставшуюся единицу первого неполного делимого переводят в другой разряд – из сотен в десятки:

М3А, ч.2, стр.31

Частный случай деления трехзначного числа на однозначное с 0 на конце; в середине делимого.

Программа Л.Г. Петерсон

По программе Л.Г. Петерсон данный прием дети начинают изучать в 3 классе.

На странице 10 начинает новая тема «Деление на однозначное число».

На странице 11 даётся случай, когда первое неполное делимое будет двузначным.

М3П,ч.2, стр. 16

На последующем уроке рассматривается частный случай, когда в середине частного получается круглое число.

М3П,ч.2, стр. 19

Рассматривается случай письменного деления на однозначное число, когда в конце делимого стоит 0, и в частном получается тоже в конце 0.

М3П,ч.2,стр.31

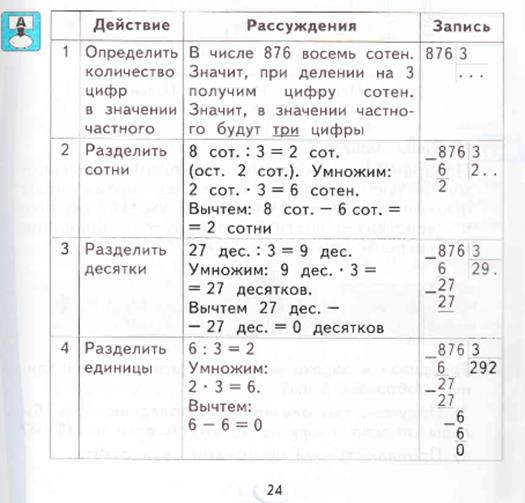
4 сотни можно разделить на 3 так, чтобы в частном получились сотни (однозначное число, отличное от 0).Значит, первое неполное делимое – 4 сотни. В частном будет три цифры, т.к. сотни стоят на третьем месте справа. Делим 4:3, возьмем по 1. Узнаем, сколько сотен разделили. Для этого 1*3=3.Узнаем, сколько сотен не разделили. Для этого из 4 – 3=1 сотня. Сравним остаток с делителем, 1

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

ДЕЛЕНИЕ, КОГДА ПЕРВОЕ НЕПОЛНОЕ ДЕЛИМОЕ — ДВУЗНАЧНОЕ ЧИСЛО

Описание презентации по отдельным слайдам:

Описание слайда:

ДЕЛЕНИЕ, КОГДА ПЕРВОЕ НЕПОЛНОЕ
ДЕЛИМОЕ — ДВУЗНАЧНОЕ ЧИСЛО

Описание слайда:

Пример: 258 : 3
1. Определяем первое неполное делимое. 2 на 3
разделить нельзя, поэтому берём две цифры делимого — 25. Это и есть первое неполное дели-мое.

Описание слайда:

2. Определяем количество цифр в частном. Их будет
две: десятки и единицы.

Описание слайда:

3. Делим первое неполное делимое 25 на 3. Ближайшее наименьшее число, которое делится на 3
без остатка, — 24. 24 : 3 = 8. Записываем в частном
первую цифру — 8. Из 25 вычитаем 24, находим
остаток 1.

Описание слайда:

Описание слайда:

5. Сносим 8. Второе неполное дели мое — 18. Делим 18 на 3. Получилось 6. Записываем цифру 6
в частном и находим остаток: 18 – 18 = 0, остатка
нет. Число поделилось полностью.

Описание слайда:

6. Читаем ответ: частное равно 86.

Описание слайда:

ДЕЛЕНИЕ ЧИСЕЛ, ОКАНЧИВАЮЩИХСЯ
НУЛЯМИ (КРУГЛЫХ ЧИСЕЛ)

Деление круглых чисел выполняется по тем же правилам.
Последняя цифра (0) просто переносится из делимого в частное.

Описание слайда:

Проверь начало решения и закончи деление.

Описание слайда:

Проверь начало решения и закончи деление.
2
1 4

Описание слайда:

Описание слайда:

Описание слайда:

Описание слайда:

Описание слайда:

Проверь правильность решения двух примеров и реши
третий самостоятельно.

Описание слайда:

Запиши, сколько цифр будет в каждом частном.

Описание слайда:

Запиши, сколько цифр будет в каждом частном.

143 920 : 2 = 71 960

3 284 480 : 4 = 821 120

Описание слайда:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Работа по теме «Развитие внимания в процессе обучения в начальной школе»

Технологическая карта урока окружающего мира по теме ««Болото и его обитатели» »

ПИСЬМЕННОЕ ДЕЛЕНИЕ НА ОДНОЗНАЧНОЕ ЧИСЛО (ДЕЛЕНИЕ В СТОЛБИК)

Технологическая карта урока математики по теме ««Числа от 1 до 10.Закрепление изученного материала» »

Проверочная работа «Имя существительное»

Презентация по математике на тему «ДЕЛЕНИЕ С ОСТАТКОМ»

Работа с безударными гласными.

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5333097 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В Якутии школьников отправили на дистанционку из-за морозов

Время чтения: 1 минута

В России стартовал прием заявок на конкурс для журналистов-школьников «Медиабум»

Время чтения: 2 минуты

В Госдуме предлагают сделать бесплатным проезд на общественном транспорте для детей до 16 лет

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

На новом «Уроке цифры» школьникам расскажут о разработке игр

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Чёрная пятница

На все курсы повышения квалификации и профессиональной переподготовки

Источник