что такое неоднородная система линейных уравнений
Что такое неоднородная система линейных уравнений
– перестановка строк матрицы;
– умножение строк матрицы на действительное отличное от руля число;
– поэлементное сложение строк матрицы;
– вычеркивание нулевой строки;
– транспонирование матрицы (в этом случае преобразования производятся по столбцам).
Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений.
Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют.
На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема.
Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть
Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными.
Если r n (количество переменных в системе больше количеств а уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций.
1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n — r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид:
2. Из коэффициентов при базисных переменных составить минор (базисный минор), который должен быть отличен от нуля.
3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля.
4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением.
5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений.
6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных.
Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений
Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:
Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования:
По формулам (1.6) имеем
Данное выражение базисных переменных через свободные представляет собой общее решение системы:
Структура общего решения системы уравнений
Однородная система линейных уравнений
Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.
Свойства решений однородной системы уравнений
1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.
В самом деле, из равенств следует, что
т.е. линейная комбинация решений является решением однородной системы.
Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.
Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец
Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.
Итак, обратное утверждение доказано.
Алгоритм решения однородной системы уравнений
1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).
6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).
7. Записать общее решение однородной системы по формуле (5.14).
1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.
2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде
3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы
Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.
Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы
Решение. 1. Составляем расширенную матрицу системы
Пункт 3 метода Гаусса пропускаем.
5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы
В результате получили фундаментальную систему решений
7. Записываем общее решение однородной системы по формуле (5.14):
Несмотря на различия, обе формулы задают одно и то же множество решений.
Структура общего решения неоднородной системы уравнений
Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.
Свойства решений неоднородной системы уравнений
1. Разность двух решений и неоднородной системы есть решение однородной системы.
2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде
В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.
Теорема 5.4 о структуре общего решения неоднородной системы.
Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец
Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.
Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.
Алгоритм решения неоднородной системы уравнений
1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).
6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.
7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.
8. Записать общее решение неоднородной системы по формуле (5.15).
2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы
Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде
где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.
Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы
Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:
Переменные — базисные, а — свободные.
7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):
8. Записываем по формуле (5.15) общее решение неоднородной системы
Искомая структура множества решений найдена.
Записываем частное решение неоднородной системы
и составляем фундаментальную матрицу:
По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):
29. Неоднородные системы линейных уравнений. Свойства их решений. Построение общего решения нслу.
Структура общего решения неоднородной системы уравнений
Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.
Рассмотрим неоднородную систему 

Свойства решений неоднородной системы уравнений
1. Разность двух решений 

Действительно, из равенств 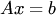


2. Пусть 



В самом деле, для любого решения 
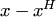

Теорема 5.4 о структуре общего решения неоднородной системы.
Пусть 

при любых значениях [i]произвольных постоянных 



Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.
Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.
Алгоритм решения неоднородной системы уравнений
1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).
6. Найти частное решение 
7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему 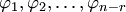

8. Записать общее решение неоднородной системы по формуле (5.15).
1. Используя фундаментальную матрицу 


где 

2. Если базисный минор матрицы 


Тогда блочная матрица 
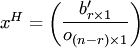
где 
Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы
Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:
Переменные 

6. Полагая 

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):
8. Записываем по формуле (5.15) общее решение неоднородной системы
Искомая структура множества решений найдена
Получим формулу общего решения вторым способом, используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:
Записываем частное решение неоднородной системы

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):
Что такое неоднородная система линейных уравнений
Решением системы называется совокупность n значений неизвестных
при подстановке которых все уравнения системы обращаются в тождества.
Система линейных уравнений может быть записана в матричном виде:
где A — матрица системы, b — правая часть, x — искомое решение, Ap — расширенная матрица системы:

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Однородной системой линейных уравнений называется система, правая часть которой равна нулю:
Матричный вид однородной системы: Ax=0.
Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.
Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.
ПРИМЕР 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей.
Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.
ПРИМЕР 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизестными.
Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.
Исследуем однородную систему методом Гаусса.
матрица исследуемой однородной системы, ранг которой r
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
19.Неоднородные слау. Теорема о представлении решения неоднородной системы. Алгоритм решения неоднородных систем.
Выясним, чем отличается решение произвольной неоднородной системы алгебраических уравнений от решения однородной системы.
Определение. Однородная система линейных алгебраических уравнений называется соответствующей неоднородной системе, если коэффициенты при неизвестных у них одинаковые, а свободные члены неоднородной системы заменены нолями.
Рассмотрим произвольную совместную неоднородную систему линейных алгебраических уравнений:
Пусть у нее в общем случае 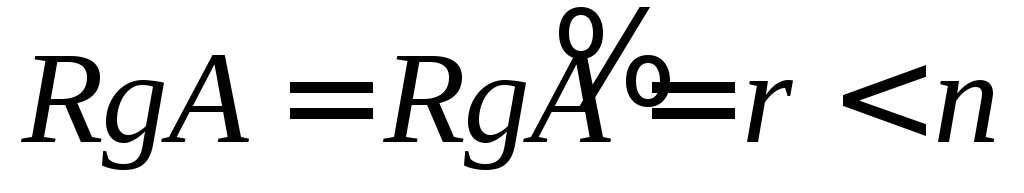
Теорема 4.1. Сумма любого решения неоднородной системы линейных алгебраических уравнений с любым решением соответствующей ей однородной системы является решением неоднородной системы.
Доказательство. Возьмем произвольное решение неоднородной системы



Если данная сумма является решением неоднородной системы, то она должна превратить в тождество любое ее уравнение:
что и требовалось доказать.
Теорема 4.2. Разность любых двух решений неоднородной системы линейных алгебраических уравнений является решением соответствующей однородной системы.
Доказательство. Возьмем два произвольных решения неоднородной системы линейных алгебраических уравнений:


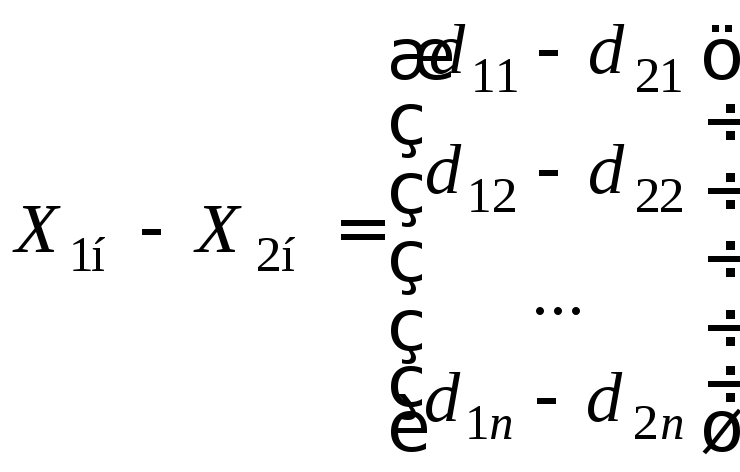
Подставим полученную разность в любое уравнение неоднородной системы:
Так как левая часть уравнения обратилась в ноль, значит, 
Из теоремы 4.2 следует, что если 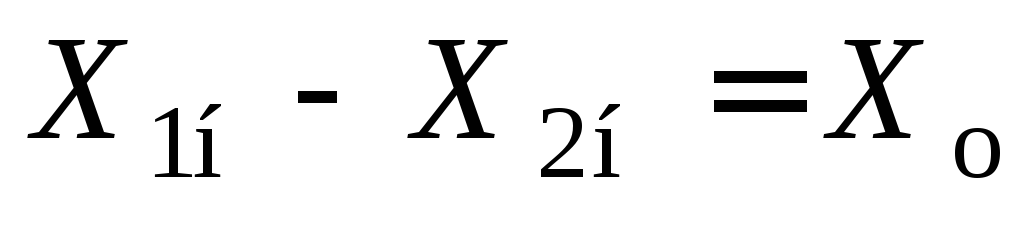



Следствие. Общее решение неоднородной системы линейных алгебраических уравнений равно сумме какого-то частного ее решения и общего решения соответствующей однородной системы.





















