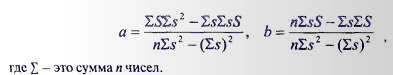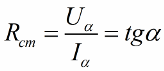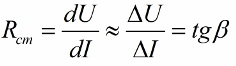Датчики и сенсоры онлайн журнал

Практика использования, теоретические основы и современные тенденции

НЕЛИНЕЙНОСТЬ

Нелинейность определяется для сенсоров, передаточную функцию которых возможно аппроксимировать прямой линией (уравнение (2.1)). Под нелинейностью понимается максимальное отклонение L реальной передаточной функции от аппроксимирующей прямой линии. Под термином «линейность» на самом деле понимается «нелинейность».

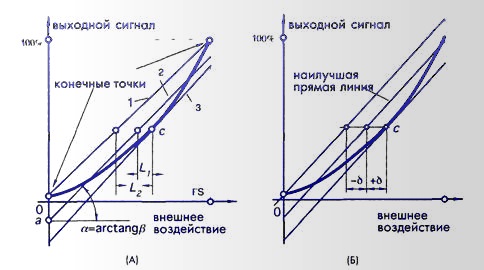
При проведении нескольких циклов калибровки выбирается худшее из полученных значений нелинейности. нелинейность обычно выражается либо в процентах от максимального входного сигнала, либо в единицах измеряемых величин (к примеру, в кПа или °С). В зависимости от способа проведения аппроксимирующей линии различают несколько типов линеаризации. Один из способов — проведение прямой через конечные точки передаточной функции (рис. 2.5А). Для этого сначала определяются выходные значения, соответствующие наибольшему и наименьшему внешним воздействиям, а потом через эти точки проводится прямая линия (линия 1). При такой линеаризации ошибка нелинейности минимальна в конечных точках и максимальна где-то в промежутке между ними.

Другой способ линеаризации основан на применении метода наименьших квадратов (линия 2 на рис. 2.5А). Для этого в широком диапазоне измеряемых величин (лучше в полном диапазоне) для ряда значений (п) внешних воздействий s измеряются выходные сигналы S. После чего, применяя формулу линейной регрессии, определяют значения коэффициентов а и Ь:

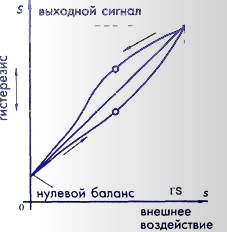
Рис. 2.4 Передаточная функция с гистерезисом

На практике, в некоторых случаях, может потребоваться большая точность линеаризации в узком диапазоне входных сигналов. к примеру, медицинские термометры должны обладать повышенной точностью в диапазоне 37°С. 38°С. Вне этой зоны точность может быть несколько ниже. В этом случае калибровку проводят в узкой области, где требуется повышенная точность, после чего через калибровочную точку с проводится аппроксимирующая линия (линия 3 на рис. 2.5А).

В результате такой процедуры наименьшее значение нелинейности достигается в зоне калибровочной точки, а ближе к концам диапазона измерения линейность значительно ухудшается. Как видно из рисунка, в данном методе аппроксимирующая линия часто является касательной к передаточной функции в точке калибровки с. Если известно выражение для реальной передаточной функции, наклон этой линии может быть найден по уравнению (2.5).

Рис. 2.5 Линейная аппроксимация нелинейной передаточной функции (А) и независимая линеаризация (Б)

Метод независимой линеаризации часто называется «методом наилучшей прямой» (рис. 2.5Б). Он заключается в нахождении линии, проходящей посередине между двумя параллельными прямыми, расположенными, как можно, ближе друг к другу и охватывающими все выходные значения реальной передаточной функции.

В зависимости от метода линеаризации аппроксимирующие линии будут иметь разные коэффициенты а и Ъ. Следовательно, значения нелинейности, полученные разными способами, могут серьезно различаться друг от друга.

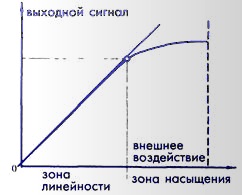
Рис. 2.6 Передаточная функция с насыщением

Информация исключительно в ознакомительных целях. При использовании материалов этого сайта ссылка обязательна.Правообладатели статей являются их правообладателями.

По вопросам размещения статей пишите на email:

Источник

Базовые метрологические понятия о весах

Дискретность:

Пример: Например, если дисплей весов показывает вес 1 кг, то при добавлении груза весом 3 г показания будут равны 1,005 кг, т.е. будут меняться с дискретностью d = 5 г. Многие ошибочно полагают, что эта величина d и является погрешностью измерения веса. Однако это не так.

Погрешность или цена поверочного деления

Наибольший предел взвешивания (НПВ)

НПВ это верхняя граница предела взвешивания. НПВ определяет самую большую массу при взвешивании на весах за один раз.

Наименьший предел взвешивания (НмПВ)

НмПВ Очень важно знать, от какого наименьшего предела взвешивания производитель гарантирует указанную в руководстве по эксплуатации погрешность весов. Знать наименьший предел взвешивания принципиально важно, т.к. весы индицируют вес на дисплее даже в случае, если измеряемый вес меньше НмПВ, однако достоверными эти показания считать нельзя.

Класс точности

С 01.07.2001 г. вступил в действие новый ГОСТ 24104-2001 (взамен ГОСТ 24104-1988). Этот ГОСТ разработан на основе международных рекомендаций OIML и подразделяет весы на 3 класса точности:

Калибровка и поверка

Это процедура регулировки цены деления весов.

Часто путают калибровку с поверкой весов. Поверка осуществляется, как правило, раз в год независимыми метрологическим службами (ЦСМ). Поверку производят с целью определения и подтверждения соответствия весов установленным техническими требованиями (ГОСТов, ТУ )

Бывает так, что потребители «довольствуются» этим и не осуществляют калибровку весов, хотя процедура эта – ежедневная. Более того, чем выше класс точности весов, тем чаще придется их калибровать в течение дня.

Калибровка бывает следующих видов:

Классы гирь

Также как и весы, калибровочные гири делятся на несколько классов. Если подходить упрощенно, то чаще всего для типичных весов, находящихся в современных лабораториях, используются гири:

Разумеется, допускается использование гирь более высокого класса для калибровки весов более низкого класса.

Повторяемость или среднеквадратическое отклонение (СКО)

СКО основано на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической. СКО показывает, насколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.

Защита весов по IP

Чтобы охарактеризовать допустимые условия эксплуатации конкретного электротехнического оборудования, для него устанавливается т.н. класс защиты IP (International Protect). Он кодируется двухзначным (или трехзначным) числом, каждая из цифр которого указывает (по условленной шкале) степень допустимого внешнего воздействия на данное изделие. Название норматива имеет вид IP XY, где первая цифра X указывает степень защиты от пыли и поражения электрическим током, а вторая Y — от воды.

Источник

Чем более линеен выходной сигнал датчика, тем проще его откалибровать и минимизировать неопределенность при масштабировании выходного сигнала

Большинство датчиков с аналоговым выходным сигналом имеют общие характеристики, такие как линейность (или нелинейность), воспроизводимость и разрешающая способность; для них также указываются факторы окружающей среды, такие как рабочая температура, ускорение и вибрация, и динамические характеристики, такие как время отклика или полоса пропускания.

Все эти характеристики представляют пределы погрешностей либо указывают источники неопределенностей, искажающих идеализированную зависимость выходного сигнала датчика от входного воздействия. Многие из этих терминов довольно легко понять только по их определениям, но нелинейность не относятся к этой категории.

Определение нелинейности датчика

Нелинейность является мерой максимального отклонения выходного сигнала датчика от заданной идеализированной (теоретической) прямой, проведённой на графике зависимости величины аналогового выходного сигнала датчика от величины входного параметра, называемого измеряемой величиной, при постоянных условиях окружающей среды. Чем выше линейность датчика, тем проще его калибровка и минимизация неопределенности при масштабировании его выходного сигнала. Однако для понимания такой характеристики датчика, как нелинейность, требуется разобраться в сущности опорной прямой.

Опорная прямая

Существует несколько возможных опорных прямых, которые можно использовать для выражения нелинейности датчика. Оптимальным выбором, основанным на статистике, была бы «линия наилучшего соответствия». Но что является критерием «наилучшего соответствия»? Как опыт, так и статистика указывают на то, что предпочтение следует отдать прямой линии, рассчитанной «методом наименьших квадратов», посредством которого сумма квадратов отклонений от желаемой прямой математически минимизируется. Такая прямая линия наилучшего соответствия (best fit straight line, BFSL) широко используется в качестве основы для выражения нелинейности датчика не только потому, что она статистически приемлема, но и потому, что она была подтверждена в реальных измерениях.

Влияние иных источников погрешностей

Поскольку нелинейность непосредственно влияет на аналоговый выходной сигнал измерительной системы, необходимо учитывать и другие источники ошибок, также способные повлиять на выходной сигнал, помимо нелинейности датчика. Чтобы полностью понять, что на самом деле означают характеристики нелинейности датчика, необходимо отметить несколько предварительных условий, которые должны выполняться в процессе измерений.

Во-первых, факторы окружающей среды, такие как температура, должны быть достаточно постоянными, либо их изменения должны быть незначительными, чтобы вызванные ими погрешности были малы по сравнению с величиной нелинейности. Во-вторых, погрешности воспроизводимости и гистерезиса в самом датчике также должны быть малы по сравнению с его нелинейностью. В-третьих, любая нелинейность на выходе системы, обусловленная её узлами, обрабатывающими сигнал от датчика, также должна быть во много раз меньше нелинейности датчика. И, наконец, разрешающая способность, как датчика, так и прибора для считывания выходных данных, должна быть достаточной, чтобы реагировать на небольшие отклонения в выходном сигнале, вызванные нелинейностью датчика.

Зачем учитывать иные источники погрешностей

Величины погрешностей измерения не могут быть просто сложены арифметически, их следует суммировать векторно (как корень квадратный из суммы их квадратов). Таким образом, только если все иные погрешности малы в сравнении с нелинейностью, то именно она будет доминирующим источником неопределенности измерений, в противном случае влияние остальных погрешностей будет решающим.

Это также одна из причин того, что измерение нелинейности датчика сложнее, чем кажется на первый взгляд. Необходимо не только иметь возможность свести к минимуму влияние факторов окружающей среды, таких как температура и влажность, также важно отметить, что нелинейность датчика должна измеряться с помощью оборудования, погрешность которого, по крайней мере, в десять раз ниже требуемой величины нелинейности самого датчика, что обычно означает высокоточные приборы, доступные, как правило, только лабораториям метрологической поверки или национальных стандартов.

Как выражается нелинейность датчиков

Максимальное значение нелинейности при использовании прямой линии наилучшего соответствия в качестве опорной для датчика с однополярным выходным сигналом обычно выражается в процентах (±) от полной шкалы выхода (Full Scale Output, FSO). Для датчика с биполярным выходным сигналом максимальная нелинейность выражается в (±) процентах от полного выходного диапазона (Full Range Output, FRO), т. е. от (–) FSO до (+) FSO.

Пример

Чтобы проиллюстрировать влияние нелинейности, рассмотрим датчик перемещения с диапазоном измерения от 0 до 2 дюймов, выходным диапазоном от 0 до 10 В постоянного тока и нелинейностью, составляющей ±0.25% FSO. Датчик имеет чувствительность 5 вольт на дюйм и FSO 10 В постоянного тока, поэтому нелинейность может привести к ошибке на выходе до ±25 мВ, что эквивалентно погрешности измерения ±0.005 дюйма. Затем пользователь должен решить, приемлема ли такая величина ошибки.

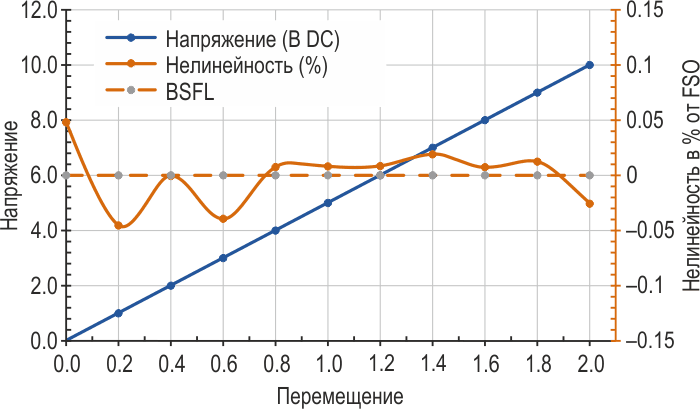Рисунок 1.	Зависимость нелинейности от выходного сигнала.

Это иллюстрируется Рисунком 1, на котором показаны как график зависимости аналогового сигнала датчика от перемещения (синяя линия), так и величина нелинейности относительно опорной линии в отдельных точках (оранжевая кривая). Имейте в виду, что величина нелинейности настолько мала, что её влияние непосредственно на синюю линию в данном масштабе незаметно.

Краткие выводы

Перевод: Вишняков Кирилл по заказу РадиоЛоцман

Источник

Линейные и нелинейные элементы электрической цепи

Те элементы электрической цепи, для которых зависимость тока от напряжения I(U) или напряжения от тока U(I), а также сопротивление R, постоянны, называются линейными элементами электрической цепи. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью.

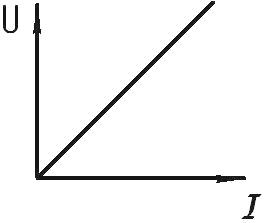
Для линейных элементов характерна линейная симметричная вольт-амперная характеристика (ВАХ), выглядящая как прямая линия, проходящая через начало координат под определенным углом к координатным осям. Это свидетельствует о том, что для линейных элементов и для линейных электрических цепей закон Ома строго выполняется.

Яркий пример линейного элемента — проволочный резистор. Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.

Характеристика проводника (вольтамперная характеристика) — зависимость между напряжением, подводимым к проводнику, и силой тока в нем (обычно выраженная в виде графика).

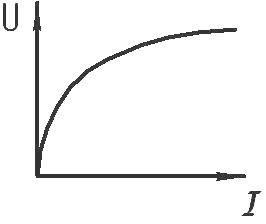
Для металлического проводника, например, сила тока в нем пропорциональна приложенному напряжению, и поэтому характеристика представляет собой прямую линию. Чем круче идет прямая, тем меньше сопротивление проводника. Однако некоторые проводники, в которых ток не пропорционален приложенному напряжению (например, газоразрядные лампы), имеют более сложную, не прямолинейную вольтамперную характеристику.

Если же для элемента электрической цепи зависимость тока от напряжения или напряжения от тока, а также сопротивление R, непостоянны, то есть изменяются в зависимости от тока или от приложенного напряжения, то такие элементы называются нелинейными, и соответственно электрическая цепь, содержащая минимум один нелинейный элемент, окажется нелинейной электрической цепью.

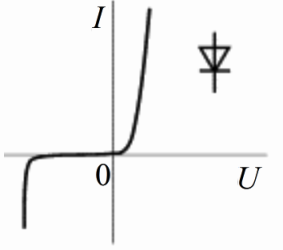
Вольт-амперная характеристика нелинейного элемента уже не является прямой линией на графике, она непрямолинейна и часто несимметрична, как например у полупроводникового диода. Для нелинейных элементов электрической цепи закон Ома не выполняется.

В данном контексте речь может идти не только о лампе накаливания или о полупроводниковом приборе, но и о нелинейных индуктивностях и емкостях, у которых магнитный поток Ф и заряд q нелинейно связаны с током катушки или с напряжением между обкладками конденсатора. Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.

Пример нелинейного элемента — лампа накаливания. С ростом тока через нить накаливания лампы, ее температура увеличивается и сопротивление возрастает, а значит оно непостоянно, и следовательно данный элемент электрической цепи нелинеен.

Такой подход делает возможным простейший анализ и расчет простых нелинейных цепей.

На рисунке выше показана ВАХ типичного диода. Она располагается в первом и в третьем квадрантах координатной плоскости, это говорит нам о том, что при положительном или отрицательном приложенном к p-n-переходу диода напряжении (в том или ином направлении) будет иметь место прямое либо обратное смещение p-n-перехода диода. С ростом напряжения на диоде в любом из направлений ток сначала слабо увеличивается, а после резко возрастает. По этой причине диод относится к неуправляемым нелинейным двухполюсникам.

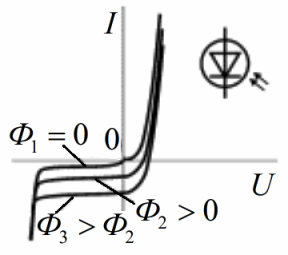
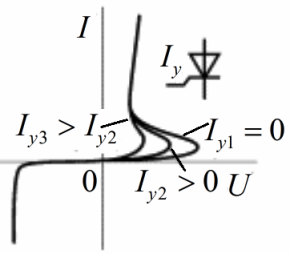
Это ВАХ тиристора, здесь видна ее явная зависимость от величины тока управляющего электрода. В первом квадранте — рабочий участок тиристора. В третьем квадранте начало ВАХ — малый ток и большое приложенное напряжение (в запертом состоянии сопротивление тиристора очень велико). В первом квадранте ток велик, падение напряжения мало — тиристор в данный момент открыт.

Момент перехода из закрытого — в открытое состояние наступает тогда, когда на управляющий электрод подан определенный ток. Переключение из открытого состояния — в закрытое происходит при снижении тока через тиристор. Таким образом, тиристор — это управляемый нелинейный трехполюсник (как и транзистор, у которого ток коллектора зависит от тока базы).

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник