что такое мощность множества в информатике
Мощность множества

В рассмотренных выше примерах |Х| = 5, |М| = 5.
Число элементов объединения двух непересекающихся множеств равно сумме чисел элементов этих множеств. Так, в объединении множеств М и X содержится 10 элементов: |М ∪ Х| = 10.

Для случая объединения трёх множеств формула имеет вид:
Аналогичные формулы справедливы и для пересечения множеств:


В зимний оздоровительный лагерь отправляется 100 старшеклассников. Почти все они увлекаются сноубордом, коньками или лыжами. При этом многие из них занимаются не одним, а двумя и даже тремя видами спорта. Организаторы выяснили, что всего кататься на сноуборде умеют 30 ребят, на лыжах — 28, на коньках — 42. Всего умением кататься на лыжах и сноуборде из них могут похвастаться 8 ребят, на лыжах и коньках — 10, на сноуборде и коньках — 5, но только трое из них владеют всеми тремя видами спорта. Сколько ребят не умеет кататься ни на сноуборде, ни на лыжах, ни на коньках?
Обозначим через S, L и К множества сноубордистов, лыжников и любителей коньков соответственно. Тогда |S| = 30, |L| = 28 и |К| = 42. При этом |S ∩ L| = 8, |К ∩ L| = 10, |S ∩ К| = 5, |S ∩ L ∩ K| = 3.
Объединение множеств S, L и К — это множество ребят, увлекающихся хотя бы каким-то видом спорта.
По формуле включений-исключений находим:
Таким образом, из 100 старшеклассников 20 не умеют кататься ни на сноуборде, ни на лыжах, ни на коньках.
Python и теория множеств
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:
Для создания пустого множества нужно непосредственно использовать set() :
Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).
Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
Объекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два «равных» объекта.
Скорее всего мы предполагаем, что объекты City(«Moscow») должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City :
Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
Свойства множеств
Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:
Принадлежность множеству
Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.
Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
Непересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.
Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
Пустое множество является подмножеством абсолютно любого множества.
Само множество является подмножеством самого себя.
Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
Добавление элементов в множество
Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
Удаление элементов из множества
Симметрическая разность множеств
Симметрическая разность множеств – это множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Также симметрическую разность можно рассматривать как разность между объединением и пересечением исходных множеств.
Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Мощность множества
Содержание
Определения [ править ]
| Определение: |
| Если А и В — произвольные множества, и между ними можно установить биекцию, то они равномощны: [math] |A| = |B| [/math] |
| Определение: |
| Множество называется конечным, если его элементы можно пересчитать, иначе оно называется бесконечным. |
Мощность счетных множеств минимальна по сравнению с другими бесконечными множествами.
Мощность Q [ править ]
[math] B \subset A [/math]
[math] a_1 \in A \Rightarrow A \backslash \ < a_1 \>= A_1 [/math] — бесконечное множество.
[math] a_2 \in A_1 \Rightarrow A_1 \backslash \ < a_2 \>= A_2 [/math] — также бесконечное множество.
Для счетных множеств часто применяется следующий важный факт:
Выпишем все элементы этих множеств в таблицу:
[math] \begin
Будем нумеровать их по диагоналям: [math] \begin
В частности, множество рациональных чисел [math] \mathbb Q [/math] — счетно.
Континуум [ править ]
Будем доказывать от противного. Применим принцип вложенных отрезков:
В результате выстраивается система вложенных отрезков:
[math] \ < \Delta_n : \Delta_
По свойству системы вложенных отрезков:
[math] \exists d = \bigcap\limits_
Мощность R [ править ]
Применим следующий прием:
Между счетными множествами можно установить биекцию: [math] B \leftrightarrow A \Rightarrow (0, 1) \backslash A \leftrightarrow [0, 1] \backslash B \Rightarrow (0, 1) \leftrightarrow [0, 1] \Rightarrow |(0, 1)| = |[0, 1]| [/math]
В итоге получили, что [math] |\mathbb R| = |[0, 1]| [/math]
Так как [math] \mathbb Q [/math] — счетно. [math] |\mathbb R \backslash \mathbb Q| = |I| \Rightarrow [/math] иррациональных чисел по мощности континииум.
1.3 Понятие о мощности множеств
Часто возникает необходимость сравнивать множества по числу элементов. В этом случае возникает понятие мощности множества.
Определение. Множества А и В называются эквивалентными (обозначается А
В) если существует биекция f: А
Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда они имеют одинаковое число элементов. Если два множества бесконечны и между ними можно установить в.о.с., то они обладают также чем-то общим, что мы будем называть мощностью. Итак, любые два эквивалентных множества (конечные или бесконечные) имеют одинаковую мощность или являются равномощными. Или более точное определение.
Определение. Мощностью множества А называется класс всех множеств, эквивалентных множеству А (мощность обозначается 
Имеется три возможности:
в) существуют бесконечные множества, которые нельзя привести во в.о.с. с множеством натуральных чисел. Например, установлено, что множество всех действительных чисел отрезка [0,1] не является счётным (теорема Кантора). Принято мощность этого множества называть континуум (часто обозначается с), а множества такой мощности континуальными.
Доказано, что если А континуальное множество, то 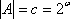


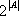
Примеры счётных множеств:
а) множество целых чисел Z, а также 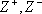
б) множество рациональных чисел Q;
в) любое бесконечное подмножество множества N, например, <2,4,6,8,…>;
г) 

Примеры континуальных множеств:
а) множество всех действительных чисел R или множество точек числовой оси;
б) множество всех точек плоскости (пространства) 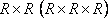
в) множество всех подмножеств счётного множества ( т.е. булеан счётного множества).
Как показано в теории множеств, для множества любой мощности множество его подмножеств имеет более высокую мощность. Поэтому не существует множества максимальной мощности. На мощность множеств можно смотреть как на новый объект, называемый кардинальным числом или кардиналом. Примерами кардиналов могут быть:
а) любое натуральное число (как мощность конечного множества);
б) 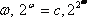
Отметим, что существование биекции между двумя множествами позволяет перенести изучение свойств с одного множества на другое, что многое упрощает, например, некоторые свойства конечного множества А, 
2 Элементы математической логики
2.1 Высказывания и логические операции
Логику чаще всего определяют как анализ методов рассуждений. Эти методы позволяют определить истинность или ложность того или иного рассуждения, причём логику интересует прежде всего форма, а не содержание доводов в этом рассуждении. Если при этом применяют математический аппарат и изучают математические рассуждения, то логику называют математической логикой. Математическая логика играет большую роль в основах математики, она – фундамент, на котором построено здание математики. Логика применяется в информатике для построения компьютерных программ и доказательства их корректности. Понятия, методы и средства математической логики лежат в основе современных информационных технологий.
Определение. Высказыванием называется повествовательное предложение, о котором в данной ситуации можно говорить, что оно истинно или ложно.
Определение. Простое (элементарное) высказывание рассматривается как некое неделимое целое. Обозначается А, В, С. Р,…; сложным (составным) называется высказывание, составленное из простых с помощью логических связок (операций).
Основными логическими операциями (связками) являются:
а) конъюкция (операция «и», логическое произведение).
Конъюнкцией двух высказываний P и Q (обозначается 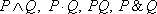
б) дизъюнкция (операция «или», логическая сумма). Дизъюнкцией двух высказываний P и Q (обозначается 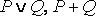
в) отрицание (инверсия). Отрицанием высказывания P (обозначается 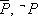
г) импликация (логическое следование). Импликацией двух высказываний P и Q (обозначается 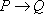
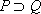
д) эквиваленция (эквивалентность). Эквиваленцией двух высказываний
Формулы алгебры логики
Рассмотрим содержание логики высказываний, используя язык алгебры логики, которая изучает строение логических высказываний (т.е. логических формул) и способы установления их истинности с помощью алгебраических методов.
Поставим в соответствие высказыванию P логическую переменную х, которая принимает значение 1, если Р истинно, 0, если Р ложно. Из логических переменных можно с помощью логических операций составлять различные конструкции, которые являются формулами алгебры логики.
а) любая логическая переменная является формулой;
б) если 
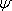
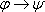
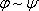
в) никаких других формул, кроме построенных в а) и б) нет.
Если формула 
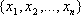
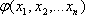
Действия логических операций задаются таблицами истинности, в каждой строке которых отмечены различные наборы значений переменных и соответствующее им значение формулы. Составим таблицы истинности логических операций в соответствии с их определением:
Мощность множества
Мощность множества, кардинальное число множества (лат. cardinalis ← cardo — главное обстоятельство, стержень, сердцевина) — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
В основе этого понятия лежат естественные представления о сравнении множеств:
До построения теории мощности множеств, множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.
Мощность множеств позволяет сравнивать бесконечные множества. Например, счётные множества являются самыми «маленькими» бесконечными множествами.
Мощность множества 




Содержание
Определение
Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощность множества — это соответствующий ему класс эквивалентности.
Комментарий
Класс множеств, биективно эквивалентных данному, не является множеством.
Связанные определения
Примеры
Свойства
См. также
Литература
Полезное
Смотреть что такое «Мощность множества» в других словарях:
Мощность множества — в математике, обобщение на произвольные множества понятия «число элементов». М. м. определяется методом абстракции как то общее, что есть у всех множеств, эквивалентных (количественно) данному; при этом два множества называемых… … Большая советская энциклопедия
МОЩНОСТЬ (в математике) — МОЩНОСТЬ множества, понятие теории множеств, обобщающее на произвольные множества понятие «число элементов». Мощность множества характеризует то общее, что присуще всем множествам, количественно эквивалентным данному; при этом два множества… … Энциклопедический словарь
мощность — и; ж. 1. к Мощный (1 5 зн.). М. голоса. М. землетрясения. Удивиться мощности животного. М. организма. М. угольного пласта. М. государства. Проверить м. армии. 2. Физ., техн. Величина, измеряемая отношением работы к промежутку времени, в течение… … Энциклопедический словарь
Мощность — 1) (в физике) некоторая физическая величина, характеризующая работу в единицу времени (имеет место в механике, электричестве, акустике, оптике и т. д.); 2) (в математике) определяют мощность множества, которая характеризует то общеелчто присуще… … Начала современного естествознания
Мощность (значения) — Мощность: Мощность (в физике и технике) отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Мощность множества (в математике) число элементов множества. Вычислительная мощность компьютера число операций,… … Википедия
МОЩНОСТЬ — кардинальное число, множества А такое свойство этого множества, к рое присуще любому множеству В, эквивалентному А. При этом два множества наз. эквивалентными (или равно мощным и), если между ними возможно установить взаимно однозначное… … Математическая энциклопедия
Мощность статистических критериев (power of tests) — Проверка гипотезы предполагает сопоставление двух конкурирующих гипотез. Нулевая гипотеза указывает на невозможность редких, необычных событий. Альтернативная гипотеза, напротив, утверждает, что такие события возможны. Напр., нулевая гипотеза… … Психологическая энциклопедия
Упорядоченные и частично упорядоченные множества — (математичексие) множества, в которых каким либо способом установлен порядок следования их элементов или, соответственно, частичный порядок. Понятия порядка и частичного порядка следования элементов определяются следующим образом. Говорят … Большая советская энциклопедия