что такое мощность континуума
Что такое мощность континуума
Определение 2. Множество Е действительных чисел называют также числовым континуумома его мощность — мощностью континуума.
Теорема (Кантор). 
Теорема утверждает, что бесконечное множество Е имеет мощность большую, чем бесконечное множество 
Покажем, что уже множество точек отрезка [0,1] несчетно.
Предположим, что оно счетно, т. е. может быть записано в виде последовательности 
Возьмем точку 
и на отрезке 
фиксируем отрезок ненулевой длины, не содержащий точку 
. В отрезке 
строим отрезок 12, не содержащий 
и если уже построен отрезок 
то, поскольку 
в нем строим отрезок 
так, что 
По лемме о вложенных отрезках найдется точка с, принадлежащая всем отрезкам 
Но эта точка отрезка 
по построению не может совпадать ни с одной из точек последовательности 
Следствия. 
и существуют иррациональные числа.
2) Существуют трансцендентные числа, поскольку множество алгебраических чисел счетно.
(После решения задачи 3, помещенной в конце параграфа, читатель, наверное, захочет переиначить последнее утверждение и сформулировать его так: «В множестве действительных чисел иногда встречаются также и алгебраические 
Уже на заре теории множеств возник вопрос о том, существуют ли множества промежуточной мощности между счетными множествами и множествами мощности континуума, и было высказано предположение, называемое гипотезой континуума, что промежуточные мощности отсутствуют.
Вопрос оказался глубоко затрагивающим основания математики. Он был окончательно решен в 1963 г. современным американским математиком П. Коэном. Коэн доказал неразрешимость гипотезы континуума, показав, что и она сама, и ее отрицание порознь не противоречат принятой в теории множеств аксиоматике, а потому гипотеза континуума не может быть ни доказана, ни опровергнута в рамках этой аксиоматики, — ситуация, вполне аналогичная независимости пятого постулата Евклида о параллельных от остальных аксиом геометрии.
Как вообразить несчетное множество?
Как известно, бесконечности бывают разных типов. Бывают счетные, бывают несчетные. Несчетные делятся на множества мощности континуум и все остальные. Счетные множества это такие, элементы которых можно упорядочить в длинный ряд и занумеровать натуральными числами. С несчетными такой фокус не удается. Тогда как же можно представить несчетное множество, в частности множество вещественных чисел [0;1)? Ответ — дерево бесконечной высоты.
Для меня несчетные множества всегда выглядели как непонятное, туманное облако символов витающее где-то на задворках мозга. Но вот недавно
облако скондесировалось в пару не слишком аккуратных, но компактных кристаллов. О них собственно и речь.
Чтобы избежать путаницы, под несчетным множеством будем подразумевать множество мощности континуум (к таким относятся вещественные числа, иррациональные числа, множество всех подмножеств натуральных чисел и другие).
Карусель
Как известно из википедии и других достоверных источников, мощность вещественных чисел отрезка [0;1) является континуумом. Вещественные числа из этого отрезка нельзя посчитать натуральными числами, т.е. сделать так чтобы одному натуральному числу соответствовало одно вещественное и наоборот. Для неверующих проведем диагональную процедуру Кантора.
Представим чисела отрезка [0,1) в двоичной системе счисления и получим набор бесконечных последовательностей единиц и нулей. 
Допустим, мы упорядочили такой набор в виде бесконечного списка как на рисунке. Упорядочив, получим квадратную таблицу в каждой ячейке которой находится либо 1, либо 0. Рассмотрим ячейки располагающиеса на главной диагонали. 
Инвертировав диагональ(000010. ) получим последовательность не попадающую в наш список, так как полученная последовательнось отличается от каждой попавшей в список хотя бы одним элементом. Последовательность номер n будет отличаться от диагональной в n-ой позиции. Следовательно, диагональная последовательность отсутствует в списке.
Исходя из приведенной схемы несчетное множество можно представлять в виде непрерывногенерируемых последовательностей. Инвертировали одну диагональную последовательность — вставили её в начало списка — сгенерировали новую и так далее. Такая карусель выглядит сомнительно.
Дерево
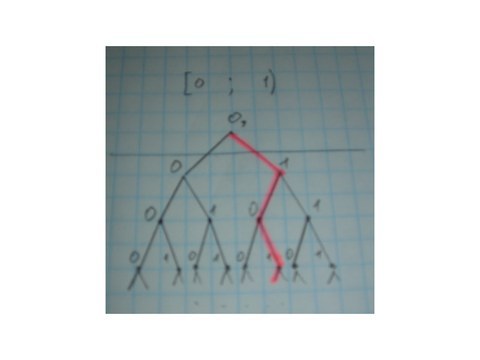
Получается, множество максимальных путей в бинарном дереве бесконечной высоты имеет мощность континуум, что эквивалентно мощности вещественных чисел отрезка [0;1).
Если вернуться к интерпретации бинарных последовательностей как двоичных дробей, то рациональные дроби вида 0,x(y) будут выглядеть в виде конечной кривулины х и бесконечной последовательности кривулин y, иррациональные числа будут выглядеть как одна бесконечная неповторяющаяся кривулина x.
Смешная загогулина
В полученном результате есть одна загвоздка: Количество путей максимальной длинны, исходящих из корня двоичного дерева бесконечной высоты несчетно. Количество же вершин такого дерева можно посчитать. Это легко сделать последовательно нумеруя вершины сверху вниз.
Для дерева конечной высоты расклад другой:
Количество путей максимальной длинны, исходящих из корня в двоичном дереве высотой N равно 2^(N-1), а количество вершин почти в два раза больше — 2^N — 1. Устремляя N к бесконечности получим, что счетная бесконечность вершин в два раза “больше” несчетной бесконечности путей.
Вот такой псевдопарадокс, иллюстрирующий работу интуиции.
Виды бесконечностей и вынос мозга
Эта статья — продолжение статьи про громадные числа. Но сейчас мы пойдем еще дальше — в бесконечности бесконечностей.
Для этого нам понадобится ZFC — теория множеств Zermelo, Frenkel + Choice. Choice — это аксиома выбора, самая спорная аксиома теории множеств. Она заслуживает отдельной статьи. Предполагается, что вы знаете, что такое «мощность» множества. Если нет, то погуглите, наверняка это изложено лучше, чем смогу я. Здесь я лишь напомню некоторые
Известные факты
Малоизвестные факты
В ZFC не все собрания элементов могут быть множествами. Бывают коллекции столь широкие, что позволить им быть множествами нельзя, возникают парадоксы. В частности, «множество всех множеств» не есть множество. Впрочем, есть теории множеств, где такие множества разрешены.
Дальше. Теория множеств… Каких объектов? Чисел? Яблок? Апельсинов? Как ни странно, ZFС не нуждается ни в каких объектах. Возьмем пустое множество <> и договоримся, что оно означает 0. 1 обозначим с помощью <<>>, двойку как <<<>>> итд. <5,2>есть <<<<<<<>>>>>>, <<<>>>>. С помощью целых чисел мы можем создать вещественные, а коллекции вещественных создают любые фигуры.
Таким образом, теория множеств это… как бы сказать… пустотелая теория. Это теория ни о чем. Точнее, о том как можно нестить (nest, то есть вкладывать друг в друга) фигурные скобки.
Единственная операция, которая определена в теории множеств, это 
— символ принадлежности. А как же объединение, исключение, равенство итд.? Все это макросы, например:
То есть, в переводе на русский язык, два множества считаются одинаковыми, когда при тестировании любого элемента на принадлежность к им мы будем получать одинаковые результаты
Множества не упорядочены, но это можно исправить: пусть упорядоченная пара (p,v) это <
,
Таким образом, теория множеств — это убогая теория без объектов и с одним значком отношения, которая обладает совершенно чудовищной силой — без каких то новых допущений она порождает из себя формальную арифметику, вещественные числа, анализ, геометрию и многое другое. Это своеобразное TOE математики.
Гипотеза континуума — CH
Существует ли мощность между 
и 
? Это проблему не мог решить Кантор, «король математиков» Гильберт высоко оценивал ее важность, но лишь позже было доказано что эту гипотезу нельзя ни доказать, ни опровергнуть. Она независима от ZFC.
Это означает, что вы можете создать две разных математики: одну с ZFC+CH, другая ZFC+(not CH). На самом деле даже больше, чем две. Допустим, мы отвергнем CH, то есть будем верить, что между и есть еще мощности. Сколько их может быть? Одна, две? Гедель верил, что только одна. Но, как оказалось, предположение о том, что их 2, 17, 19393493 не приводит к противоречиям. Любое число, но не бесконечное!
Когда в формальной арифметике мы сталкиваемся с недоказуемым утверждением, то в силу определенных причин мы знаем, что, тем не менее, это утверждение, хоть и не доказуемо, но на самом деле либо истинно, либо ложно. В теории множеств это не работает, мы реально получаем разные математики. Как к этому относиться? Есть три философских подхода:
Формализм: а чему, собственно, удивляться? Мы задаем правила игры в символы, разные правила — разный результат. Не надо искать проблему там, где ее нет
Платонизм: Но как тогда объяснить, что совершенно разные теории, например ZFC и New Foundations, построенные по совершенно разным принципам, дают почти всегда один и тот же результат? Не говорит ли это о том, что за формулами стоит какая то реальность, которую мы изучаем? Такой точки зрения придерживался, например, Гедель
Multiverse: У нас может быть много аксиоматик, иногда дающих одинаковый результат, иногда нет. Мы должны воспринимать картину в целом — если с разными системами аксиом ассоциировать цвет, то цветное дерево следствий и есть математика. Если что-то верное везде — это белый цвет, но есть и цветные ветви.
Все выше и выше.
Как далеко мы можем продвинуться? После бесконечного количества итераций мы дойдем до 
— бесконечная по порядку мощность! Кстати, ее существование было неочевидно Кантору. Но секунду! Ведь функция powerset всегда определена, поэтому не может быть последней!
Чтобы получить 
надо повторить powerset бесконечность и еще три раза. У вас уже начало сносить крышу? То ли еще будет. Потому что снова проитерировав powerset бесконечное число раз, мы дойдем до 
, после чего, естественно, идет 
Дойдя до бесконечности бесконечное число раз, мы получим индекс 
. Как вам такая мощность, например: 
? Пока мы итерировали powerset по списку ординалов, вот начальные ординалы:
но их значительно, значительно больше. Так что мы сразу все это пропустим и сделаем
Сразу большой шаг
Далее мы пойдем быстрее:
У последнего алефа индекс ноль, но местный latex не дает его поставить — слишком много уровней. Но главное вы поняли, какую бы новую чудовищную мощность мы бы не создали, мы можем сказать — ага, это всего лишь повторитель, и поставить всю эту конструкцию к новому алефу в виде индекса. Теперь мощности растут как снежный ком, нас не остановить, пирамида алефов все выше, и мы можем создать любую мощность… Или нет?
Недостижимые мощности
Что если есть мощность настолько большая, 
, что как бы мы ее ни пытались достичь «снизу», выстраивая конструкции из алефов, мы ее не достигнем? Оказывается, существование такой мощности независимо от ZFC. Вы можете принять ее существование или нет.
Я слышу шепот «бритва Оккама»… Нет, нет. Математики придерживаются противоположного принципа, который называется онтологический максимализм — пусть существует все, что возможно. Но существуют еще как минимум две причины, почему эту гипотезу хочется принять.
Второе: если отвергнуть аксиому бесконечности, то мы получим FinSet, простую игрушечную теорию множеств с конечными множествами. Давайте выпишем все эти множества (так называемая модель теории)
И получим… бесконечное множество конечных множеств… То есть, модель теории конечных множеств бесконечна, и играет в ней роль «множества всех множеств». Может быть, это поможет понять, почему теория не может говорить о «множестве всех множеств» — такое множество всегда существует как модель вне теории и обладает другими свойствами, чем множества внутри. Вы не можете добавить в теорию конечных множеств бесконечное.
И да, это «множество всех множеств» теории ZFC. В этом видео в конце очень красиво сказано про недостижимую мощность, но нам пора дальше.
Еще дальше.
Разумеется, мы можем пойти дальше, итерируя 
. Пройдя все описанные этапы, построив огромные башни повторителей, мы снова упремся в недостижимый кардинал (но теперь нам не нужны новые аксиомы, с аксиомой существования недостижимой мощности, которую мы только что добавили, это стало доказуемо). И снова и снова.
Заметьте, что теперь стрелка у нас имеет смысл не как выполнение функции Powerset(), а GetNextInaccessible(). В остальном все выглядит очень похоже, мы имеем:
Теперь то мы точно достигнем чего угодно… Или нет?
Иерархия больших мощностей.
Да, с помощью GetNextInaccessible мы упремся уже в гипер-недостижимую мощность. Существование ее требует принять еще одну аксиому. Есть и гипер-гипер-недостижимые мощности. И так далее. Но есть и другие способы определять мощности, не только через недостижимость:
За каждой ссылкой стоит, как правило, целая бесконечная иерархия с произвольным количеством приставок hyper- и повторителей. Однако, общее количество формул, определяющие недостижимые кардиналы, не такое уж большое — ведь количество формул счетно. Поэтому рано или поздно они кончатся. Там, где они кончаются, проведена красная черта. Все, что ниже этой черты, определяется более зыбко, хотя и формально.
Сама красная черта обозначает конец вселенной Геделя (но не забываем, что Гедель создал ДВЕ разные вселенные) — вселенная множеств, конструируемых «снизу» с помощью формул. Мощности выше красной черты называются хм, «малыми», а ниже — большими:
Главная идея в них в том, что вселенная множеств становится столь большой, что начинает повторять себя в разных смыслах. Каждая строчка, как всегда, требует отдельной аксиомы, и нескольких. И что еще интереснее, все это не настолько бесполезно, как вы могли подумать. Например, самая сильная аксиома (rank-into-rank), в самой нижней строчке, нужна, чтобы доказать факт о табличках.
Ниже опрос, последний вариант выбора расшифрован тут.
Мощность континуума
Конти́нуум в теории множеств — мощность (или кардинальное число) множества всех вещественных чисел. [1] Обозначается строчной латинской буквой c во фрактурном начертании: c <\displaystyle <\mathfrak 
. Множество, имеющее мощность континуум, называется континуа́льным [2] множеством.
Также термин «континуум» может обозначать само множество вещественных чисел, или даже любое континуальное множество.
Содержание
Свойства
Происхождение термина
Изначально континуумами были названы более чем одноточечные непрерывные («континуальные») порядки, то есть порядки со связной естественной топологией. В терминах собственно порядка это означает, что любое его сечение является дедекиндовым.
Континуум как целое может как иметь, так и не иметь минимального и максимального элементов, то есть его концы могут быть как «открыты», так и «замкнуты».
Минимальным (то есть содержащимся в любом континууме) континуумом является вещественная прямая (как с открытыми, так и с замкнутыми концами).
Минимальное пополнение порядка до континуума строится заполнением щелей дополнительными точками, а скачков — отрезками (0, 1) без концов.
В последующем термин «континуум», выйдя за пределы специфических порядковых рассмотрений, в теории множеств (а вслед за ней — и в остальной математике) сузился до собственно вещественной прямой, а «мощность континуума» c = c 0 <\displaystyle <\mathfrak , стала, соответственно, её мощностью. В дальнейшем «континуумом» стали называть уже саму мощность континуума c <\displaystyle <\mathfrak . В топологии этот термин, напротив, расширился до любой связной компактной хаусдорфовой топологии (связного компакта), безотносительно к тому, имеет ли данная топология порядковое происхождение, при этом некоторые континуумы в старом смысле (например, вещественная прямая с открытыми концами) перестали считаться таковыми из-за потери компактности. В настоящее время использование термина «континуум» в исходном смысле встречается в основном лишь в сравнительно старой литературе.
Примеры
Примеры множеств, имеющих мощность континуум:
Примечания
Мощность континуума
Это было доказано Георгом Кантором в его бесчисленном доказательстве 1874 года, которое является частью его новаторского исследования различных бесконечностей. Неравенство было позже сформулировано более просто в его диагональном аргументе в 1891 году. Кантор определил мощность в терминах биективных функций : два множества имеют одинаковую мощность тогда и только тогда, когда между ними существует биективная функция.
Бесчисленность
Кардинальные равенства
Кардинальное равенство c 2 знак равно c <\ Displaystyle <\ mathfrak можно продемонстрировать с помощью кардинальной арифметики :
Используя правила кардинальной арифметики, можно также показать, что
Альтернативное объяснение c знак равно 2 ℵ 0 <\ displaystyle <\ mathfrak > = 2 ^ <\ aleph _ <0>>> 
(Это верно даже в случае повторения расширения, как в первых двух примерах.)
Поскольку каждое действительное число можно разбить на целую часть и десятичную дробь, мы получаем:
где мы использовали тот факт, что
Огромное количество множеств, изучаемых в математике, имеют мощность, равную c <\ displaystyle <\ mathfrak . Вот некоторые общие примеры:
Множества с мощностью больше, чем c <\ displaystyle <\ mathfrak включать:
Все они имеют мощность 2 c знак равно ℶ 2 <\ Displaystyle 2 ^ <\ mathfrak ( Между двумя ).