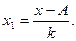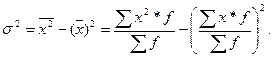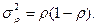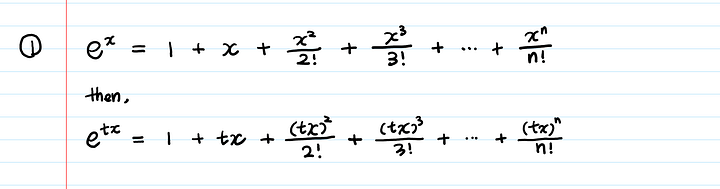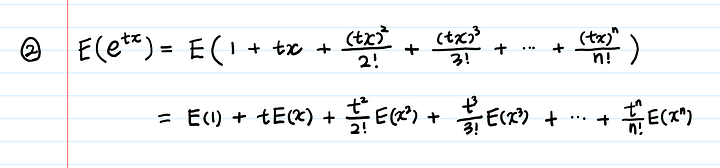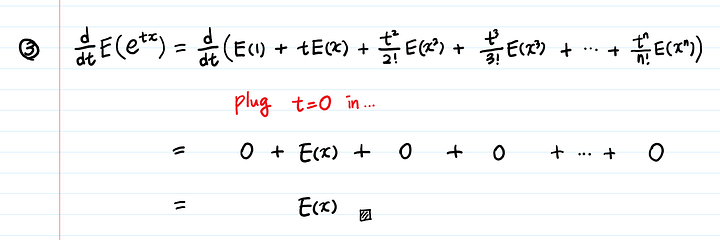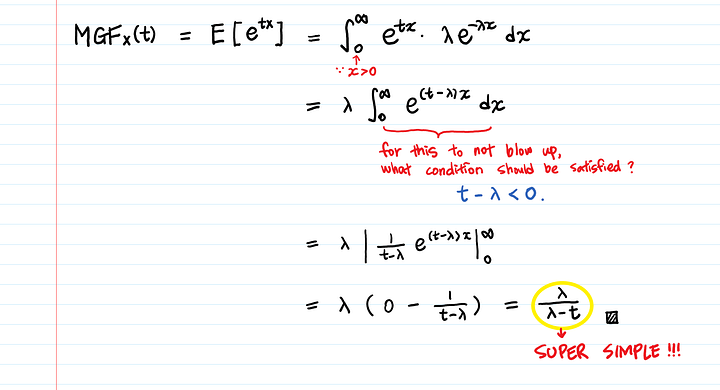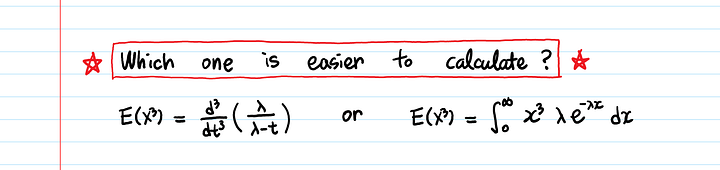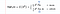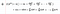что такое момент в статистике

Что такое моменты в статистике?

Моменты в математической статистике включают базовые вычисления. Эти вычисления можно использовать для определения среднего, дисперсии и асимметрии распределения вероятностей.

Использование этой формулы требует, чтобы мы были осторожны с порядком операций. Нам нужно сначала сделать экспоненты, сложить, а затем разделить эту сумму на n общее количество значений данных.

Замечание о термине «момент»

Термин момент был взят из физики. В физике момент системы точечных масс вычисляется по формуле, идентичной приведенной выше, и эта формула используется для определения центра масс точек. В статистике значения больше не являются массами, но, как мы увидим, моменты в статистике по-прежнему измеряют что-то относительно центра значений.

Сначала Момент

Для первого момента мы устанавливаем s = 1. Формула для первого момента выглядит следующим образом:

Это идентично формуле для выборочного среднего.

Первый момент значений 1, 3, 6, 10 равно (1 + 3 + 6 + 10)/4 = 20/4 = 5.

Второй момент

Для второго момента мы устанавливаем s = 2. Формула для второго момента:

Второй момент val ues 1, 3, 6, 10 равно (1 2 + 3 2 + 6 2 + 10 2 )/4 = (1 + 9 + 36 + 100)/4 = 146/4 = 36,5.

Третий момент

Для третьего момента мы устанавливаем s = 3. Формула для третьего момента:

Третий момент значений 1, 3, 6, 10 равен (1 3 + 3 3 + 6 3 + 10 3 )/4 = (1 + 27 + 216 + 1000)/4 = 1244/4 = 311.

Более высокие моменты можно рассчитать аналогичным образом. Просто замените s в приведенной выше формуле числом, обозначающим желаемый момент.

Моменты относительно среднего

Первый момент о среднем

Первый момент о среднем значении всегда равен нулю, независимо от того, с каким набором данных мы работаем. Это можно увидеть в следующем:

Второй момент о среднем

Второй момент о среднем получается из приведенной выше формулы путем установки s = 2:

Эта формула эквивалентна к этому для выборки дисперсии.

Например, рассмотрим набор 1, 3, 6, 10. Мы уже вычислили, что среднее значение этого набора равно 5. Вычтите это из каждого значения данных, чтобы получить различия:

Мы возводим каждое из этих значений в квадрат и складываем их вместе: (-4) 2 + (-2) 2 + 1 2 + 5 2 = 16 + 4 + 1 + 25 = 46. Наконец, разделите это число на количество точек данных: 46/4 = 11,5

Applications of Moments

Как упоминалось выше, первый момент — это среднее значение, а второй момент — это среднее значение — выборочная дисперсия. Карл Пирсон ввел использование третьего момента о среднем значении при вычислении асимметрии и четвертого момента о среднем значении при вычислении эксцесса.

Источник

Что такое момент в статистике

Каждая случайная величина полностью определяется своей функцией распределения.

В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.

называется величина 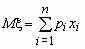, если число значений случайной величины конечно.

Если число значений случайной величины счетно, то 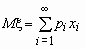. При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

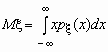
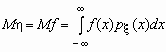
Математическое ожидание непрерывной случайной величины с плотностью вероятностей p _x (x) вычисляется по формуле . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

.

Аналогичные формулы справедливы для функций дискретной случайной величины:

, .

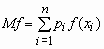
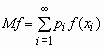
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина M x 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

, .

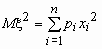
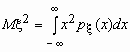
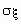
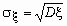
Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение , связанное с дисперсией соотношением .

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:

В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой ,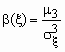

Эксцесс g случайной величины x определяется равенством .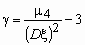

У нормального распределения, естественно, g = 0. Если g ( x ) > 0, то это означает, что график плотности вероятностей p _x (x) сильнее “заострен”, чем у нормального распределения, если же g ( x ) x (x) меньше, чем у нормального распределения.

Средним гармоническим случайной величины, принимающей положительные значения, называется величина .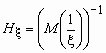

Например, для непрерывной случайной величины, распределенной равномерно на [a, b],

0 xa₁a₂a₃.a_np1/n1/n1/n.1/n

Среднее геометрическое, вычисляется следующим образом:

,

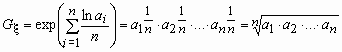
т.е. получилось традиционное определение среднего геометрического чисел a₁, a₂, …, a_n.

, .

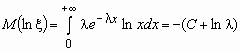
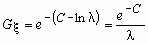
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Моменты распределения

Дисперсия: способы ее расчета, виды дисперсии, правило сложения дисперсии.

Дисперсия обладает рядом математических свойств, позволяющих упростить ее расчет.

Первое свойство заключается в том, что если из всех вариант вычесть какое-то постоянное число, то дисперсия от этого не изменится. Оно позволяет рассчитывать дисперсию не по отклонениям вариант от средней (часто имеющей дробное значение), а по отклонениям от целого числа. Второе свойство позволяет все варианты разделить на какое-то постоянное число, например на значение интервала, и исчислить дисперсию уменьшенных вариант, а полученную величину умножить на квадрат этого числа.

, .

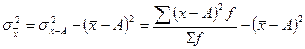
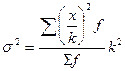
где: s 2 _x – дисперсия отклонений вариантов от средней арифметической;

– дисперсия отклонений вариантов от произвольной величины А.

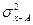
1. На этих свойствах основан расчет дисперсии способом отсчета от условного нуля или способ моментов, который заключается в нахождении вариант, уменьшенных на условно постоянную величину А и в k раз, где k – интервал, т.е. х₁=(х – А)/k, и последующем расчете дисперсии по формуле:

способ отсчета от условного нуля: ;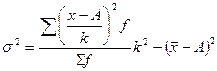

способ моментов: 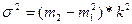, где

условный момент первого порядка: ;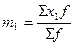

условный момент второго порядка: ,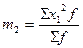

2. Дисперсия равна среднему квадрату значений признака за вычетом квадрата среднего значения признака:

Расчеты дисперсии различными способами дают одинаковые результаты, что позволяет исследователю выбрать наиболее эффективный способ.

В ряде случаев изучают не среднюю величину признака, а долю единиц, обладающих тем или иным признаком. Например, доля междугородных телефонных соединений (разговоров), предоставленных с ожиданием до 1 часа. Это примеры альтернативных вариаций, когда имеются лишь два взаимоисключающих варианта: наличие или отсутствие признака у данной единицы совокупности (1 наличие признака, 0 отсутствие). В таких случаях определяется дисперсия альтернативного признака. Пусть доля единиц, обладающих данным признаком, равна р, а доля единиц, не обладающих этим признаком, 1–р, тогда

Естественно, средняя постоянная величины р есть сама эта величина, а дисперсия равна:

Средняя и дисперсия это частные случаи более широкого понятия обобщающих характеристик любого распределения моментов.

Момент распределения – это средняя арифметическая тех или иных степеней отклонений вариантов х от некоторой постоянной величины А:

m_z = .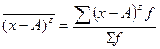

Порядок момента определяется величиной z, т.е. степенью, в которую возводится отклонение вариант. В зависимости от принятой величины А различают три вида моментов:

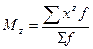
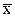
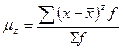
начальные (при А=0): ; центральные (при А=): ;

условные (при А≠0, А≠): .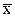

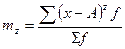
Начальный момент первого порядка представляет собой среднюю арифметическую: ;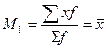

центральный момент второго порядка – дисперсию: 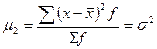. Центральный момент первого порядка m₁ всегда равен нулю (сумма отклонений вариант от средней равна нулю); центральный момент третьего порядка равен нулю в симметричном распределении.

Условные моменты самостоятельного значения не имеют, ими пользуются для упрощения вычисления центральных моментов: m₂ = m₂ – m 2 ₁; m₃ = m₃ – 3m₁ m₂ + 2m 3 ₁; m₄ = m₄ – 4m₃ m₁ + 6m₂ m 2 ₁ – 3 m 4 ₁.

Для исчисления условных моментов используется условная величина:

; ; ; ; где

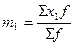
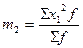
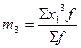
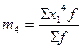
В этом случае центральные моменты корректируются на величину k z :

Наряду с изучением вариации признака по всей совокупности в целом часто возникает необходимость проследить количественные изменения признака по группам, на которые разбита вся совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных дисперсий: общей, межгрупповой, внутригрупповой и средней из внутригрупповых дисперсий.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:

.

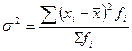
Межгрупповая дисперсияхарактеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки:

, где

— соответственно средние и численности по отдельным группам,

— средняя всей совокупности.

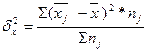
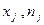
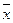
Внутригрупповая дисперсияотражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки:

, где

— варианты групп, — численность группы, — средняя группы

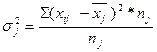
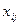
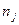
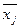
Средняя из внутригрупповых дисперсийопределяется по формуле:

.

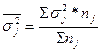
Общая дисперсия определяется как сумма средней из внутригрупповых дисперсий и межгрупповой дисперсии:

.

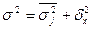
Данная сумма называется правилом сложения дисперсий.

Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием прочих факторов, и дисперсии, возникающей за счет группировочного признака.

На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результирующим признаками. Он называется эмпирическим корреляционным отношением и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии:

.

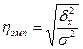
Отношения межгрупповой дисперсии к общей дисперсии называется эмпирическим коэффициентом детерминациии показывает долю группировочного признака в общей вариации:

.

Источник

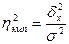
Объясняем производящую функцию моментов

1. Начнем с главного — что такое “момент” в вероятности и статистике?

Скажем, нас интересует случайная переменная X.

Моменты — это ожидаемые значения X, например, E(X), E(X²), E(X³) и т.д.

Нам очень хорошо знакомы первые два момента: математическое ожидание μ = E(X) и дисперсия E(X²) − μ². Это важные характеристики X.Математическое ожидание — это среднее значение случайной величины, дисперсия — мера разброса значений. Но должны быть и другие функции, также определяющие распределение. Например, третий момент указывает на асимметрию, четвертый — насколько тяжелы хвосты распределения.

2. Что же такое производящая функция моментов?

Глядя на определение, вы можете сказать:

Возьмите производную от ПФМ n раз и подставьте t = 0. Так вы получите E(X^n).

3. Почему n-й момент является n-й производной ПФМ?

Для доказательства используем ряды Тейлора:

Затем берем ожидаемое значение:

Теперь берем производную по t:

Если возьмем другую производную (то есть производную дважды), получим E(X²).
Снова возьмем производную (третью), получим E(X³), и так далее.

Когда я впервые увидела ПФМ, я не поняла роль t в функции, потому что t показалась произвольной переменной, которая не особенно меня интересовала. Между тем t является вспомогательной переменной — мы вводим t, чтобы использовать исчисление (производные) и обнулить значения (которые нас не интересуют).

Подождите… но мы можем вычислить моменты, используя определение ожидаемых значений. Зачем нам ПФМ?

4. Так зачем нам нужна ПФМ?

Производящая функция моментов упрощает вычисление моментов.

В моем учебнике математики написано: “найдите производящую функцию момента биномиального (n, p), пуассонового (λ), экспоненциального (λ), нормального (0, 1) распределений и так далее”. Однако в нем никогда не объяснялось, почему ПФМ полезна и удобна.

Начнем с плотности вероятности:

Продифференцируем экспоненциальную ПФМ:

Чтобы ПФМ существовала, должно существовать ожидаемое значение E(e^tx).
Вот почему t — λ — важное условие: в противном случае интеграл не будет сходиться (это называется тестом на сходимость и проверяется первым делом, когда нужно определить, сходится интеграл или расходится).

Раз у нас есть ПФМ: λ/(λ-t), вычисление моментов становится просто вопросом взятия производных, что проще, чем использование интегралов для расчета ожидаемого значения напрямую.

Используя ПФМ, можно находить моменты при помощи производных, а не интегралов!

Источник

Объясняем производящую функцию моментов

Dec 6, 2019 · 4 min read

1. Начнем с главного — что такое “момент” в вероятности и статистике?

Скажем, нас интересует случайная переменная X.

Моменты — это ожидаемые значения X, например, E(X), E(X²), E(X³) и т.д.

Нам очень хорошо знакомы первые два момента: математическое ожидание μ = E(X) и дисперсия E(X²) − μ². Это важные характеристики X. Математическое ожидание — это среднее значение случайной величины, дисперсия — мера разброса значений. Но должны быть и другие функции, также определяющие распределение. Например, третий момент указывает на асимметрию, четвертый — насколько тяжелы хвосты распределения.

2. Что же такое производящая функция моментов?

Глядя на определение, вы можете сказать:

Возьмите производную от ПФМ n раз и подставьте t = 0. Так вы получите E(X^n).

3. Почему n-й момент является n-й производной ПФМ?

Для доказательства используем ряды Тейлора:

Затем берем ожидаемое значение:

Теперь берем производную по t:

Если возьмем другую производную (то есть производную дважды), получим E(X²).
Снова возьмем производную (третью), получим E(X³), и так далее.

Когда я впервые увидела ПФМ, я не поняла роль t в функции, потому что t показалась произвольной переменной, которая не особенно меня интересовала. Между тем t является вспомогательной переменной — мы вводим t, чтобы использовать исчисление (производные) и обнулить значения (которые нас не интересуют).

Подождите… но мы можем вычислить моменты, используя определение ожидаемых значений. Зачем нам ПФМ?

4. Так зачем нам нужна ПФМ?

Производящая функция моментов упрощает вычисление моментов.

В моем учебнике математики написано: “найдите производящую функцию момента биномиального (n, p), пуассонового (λ), экспоненциального (λ), нормального (0, 1) распределений и так далее”. Однако в нем никогда не объяснялось, почему ПФМ полезна и удобна.

Я думаю, пример ниже порадует вас — самый яркий пример, где есть простое использование ПФМ: ПФМ экспоненциального распределения. (Не знакомы с экспоненциальным распределением? 👉 Экспоненциальное распределение: восприятие, происхождение, применение)

Начнем с плотности вероятности:

Продифференцируем экспоненциальную ПФМ:

Чтобы ПФМ существовала, должно существовать ожидаемое значение E(e^tx).
Вот почему t — λ — важное условие: в противном случае интеграл не будет сходиться (это называется тестом на сходимость и проверяется первым делом, когда нужно определить, сходится интеграл или расходится).

Раз у нас есть ПФМ: λ/(λ-t), вычисление моментов становится просто вопросом взятия производных, что проще, чем использование интегралов для расчета ожидаемого значения напрямую.

Используя ПФМ, можно находить моменты при помощи производных, а не интегралов!

Источник