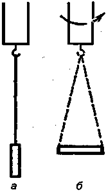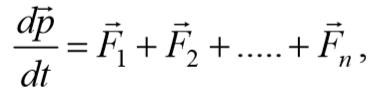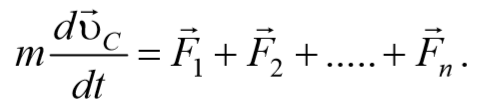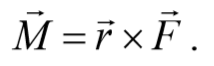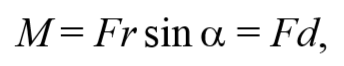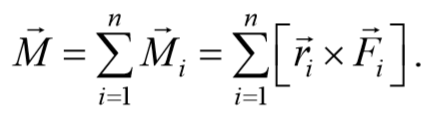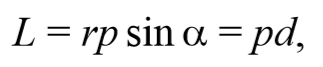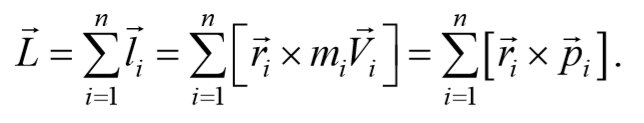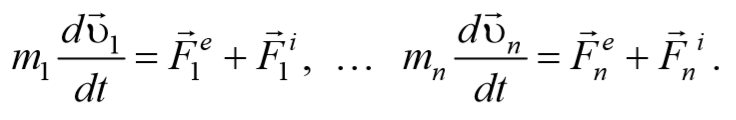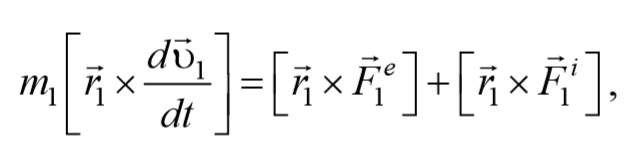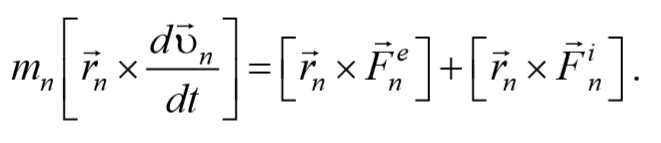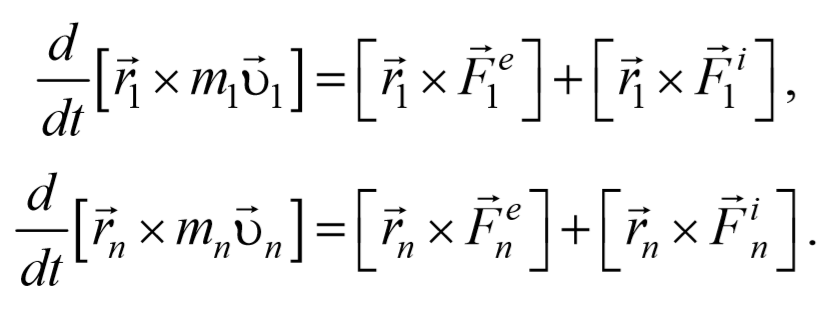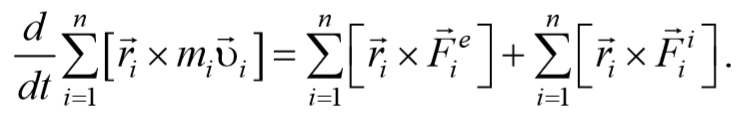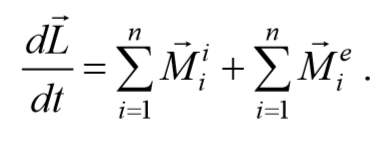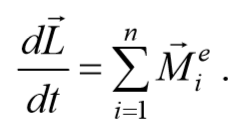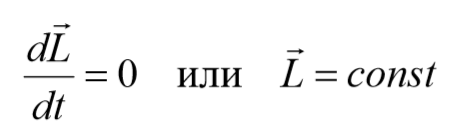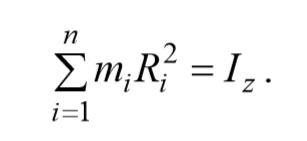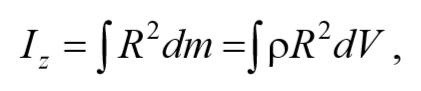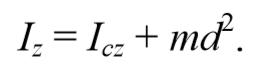что такое момент импульса тела
Савельев И.В. Курс общей физики, том I

Загрузить всю книгу 
Титульный лист
Главная редакция физико-математической литературы
Механика, колебания и волны,
КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I
Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.
Предисловие к четвертому изданию
При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.
Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.
Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.
Ноябрь 1969 г. И. Савельев
Из предисловия к четвертому изданию
Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.
При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.
Момент импульса
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Пожалуй, наибольшую роль, момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент импульса замкнутой системы сохраняется. Момент импульса является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Эта статья — об энергетическом спектре квантовой системы. О распределении частиц по энергиям в излучении см. Спектр, Спектр излучения. Об энергетическом спектре сигнала см. Спектральная плотность.Энергетический спектр — набор возможных энергетических уровней квантовой системы.
В теории поля представление системы зарядов в виде некоторых квадрупо́лей, аналогично представлению её в виде системы диполей, используется для приближённого расчёта создаваемого ей поля и излучения. Более общим представлением является разложение системы на мультиполи, соответствующее разложению потенциалов в ряд Тейлора по некоторым переменным. Квадруполь — частный случай мультиполя. Квадрупольное рассмотрение системы оказывается особенно важным в том случае, когда её дипольный момент и заряд равны.
Момент импульса тела. Изменение момента импульса
Основное уравнение вращательного движения (7.3) можно преобразовать к виду, который оказывается полезным при решении многих задач:
Выражение, стоящее в скобках, называется моментом импульса тела.
Моментом импульса ( L ) тела, вращающегося вокруг оси, называется величина, равная произведению момента инерции относительно данной оси на угловую скорость вращения:
Размерность момента импульса в СИ — кг·м 2 /с.
Примечание. В тех случаях, когда угловую скорость вращения рассматривают как вектор, момент импульса тоже является вектором. В настоящем учебнике такие случаи не рассматриваются.
С учетом этого определения выражение (7.4) принимает вид:
Важное следствие уравнения (7.6) будет рассмотрено в разделе «Законы сохранения».
Моменты инерции некоторых тел
Моменты инерции некоторых симметричных тел представлены на рис. 7.4.
Приблизительные значения моментов инерции туловища человека и его конечностей вычисляются по формулам для цилиндра или с помощью опытных данных. Для длинных звеньев конечностей моменты инерции приближенно равны 0,3 ml 2 (где т — масса звена, l — его длина). Моменты инерции элементов конечностей представлены в табл. 7.1.
На рис. 7.5 показаны моменты инерции тела относительно разных осей.
Момент инерции тела человека относительно заданной оси определяется как сумма моментов инерции всех звеньев тела относительно той же оси. Наименьший момент инерции тело человека имеет в выпрямленном состоянии относительно продольной оси тела, проходящей через его центр масс. Целенаправленное изменение момента инерции тела человека широко используется при управлении вращательными движениями в различных видах cпорта.
Рис. 7.4. Моменты инерции некоторых однородных тел
Моменты инерции элементов конечностей
| Название звена тела человека | Момент инерции, кгм 2 |
| Верхняя конечность (масса 4,2 кг) | 0,3 |
| Нижняя конечность | 1,7 |
| Большой палец руки | 0,00006 |
| Средний палец руки | 0,00014 |
| Мизинец руки | 0,00004 |
Рис. 7.5. Моменты инерции тела вокруг разных осей (в относительных единицах)
Момент инерции относительно вертикальной оси вращения, проходящей через центр масс (центр масс человека находится в саггитальной плоскости несколько впереди второго крестцового позвонка) в зависимости от положения человека, имеет следующие значения, рис. 7.6: а) 1,2 кг·м 2 — при стойке «смирно», б) 8 кг·м 2 — при стойке «арабеск», в) 17 кг·м 2 — в горизонтальном положении.
Рис. 7.6. К определению момента инерции тела в различных положениях: а) «смирно», б) «арабеск», в) горизонтальное положение
Вращательные движения без опоры.
В случае вращения вокруг свободных осей, внешнего удерживающего тела не существует. Звенья вращающегося тела спортсмена удерживаются на криволинейных траекториях внутренними связями. Ось вращения неизменно проходит через ОЦМ тела, рис. 7.7.
Рис. 7.7. Вращательное движение на перекладине и соскок дугой с сальто
При соскоке дугой с сальто вперед из положения упора на перекладине стоя согнувшись, гимнаст под действием силы тяжести совершает движение вокруг оси перекладины назад. Из позы 2, резко разгибая ноги в тазобедренных суставах и сгибая в коленных, гимнаст отпускает перекладину и переходит в позу 3. Вращательное движение вокруг свободной оси, проходящей через ОЦМ, созданное к моменту отрыва от перекладины, резко ускоряется благодаря энергичному группированию — сгибанию тела вперед. Части тела приближаются к оси вращения, уменьшают момент инерции относительно поперечной оси. По закону сохранения момента инерции до позы 5 происходит нарастание скорости. Начиная с позы 5 гимнаст распрямляет тело, момент инерции относительно поперечной оси увеличивается, и вращение вокруг нее перед приземлением замедляется, поза 6.
Свободные оси
Тело может вращаться не только вокруг закрепленной оси, но и вокруг оси, которая не закреплена. В любом теле можно выбрать такие оси, направление которых при вращении вокруг них будет сохраняться без каких либо специальных устройств (например, подшипников). Такие оси называют свободными.
Свободные оси — оси, которые без специального закрепления сохраняют свое направление в пространстве.
Пример: ось вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела.
Очевидно, что для однородных тел свободной осью является ось полной геометрической симметрии. Можно доказать, что в любом теле имеется не менее трех взаимно перпендикулярных свободных осей вращения, эти оси называются главными осями инерции. При этом оказывается, что при отсутствии внешних воздействий устойчивым является вращение тела только вокруг двух осей, относительно которых оно имеет наибольший или наименьший момент инерции. Например, если, подбросив тело, привести его во вращение относительно произвольной оси, то, падая, оно само по себе перейдет к вращению вокруг оси, которой соответствует или наибольший, или наименьший момент инерции. В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно самопроизвольно изменяет эту ось на ось с наибольшим моментом. На рис. 7.8 показана иллюстрация этого явления.
Рис. 7.8. Изменение свободной оси
Вращение человека в свободном полете и при различных прыжках происходит вокруг главной оси с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы, то при различных позах направления главных осей будут различны.
У человека из-за наличия многозвенных, большей частью открытых в ходе движения кинематических цепей, имеется большое число степеней свободы. Так, подвижность кончиков пальцев относительно грудной клетки определяется 12 степенями свободы; запястья относительно лопатки — 7; а общее число степеней свободы всего тела — трехзначное число.
На рис. 7.9. представлена упрощенная модель скелета руки. Кинематическая схема показывает подвижные звенья скелета и типы шарнирных соединений (два шаровых шарнира и один цилиндрический). Эта модель имеет семь степеней свободы: три степени свободы в плечевом поясе, одна степень свободы в локтевом суставе и три степени свободы у кисти. На динамической схеме стрелками показаны оси вращения, соответствующие этим степеням свободы.
Дата добавления: 2019-01-14 ; просмотров: 411 ; Мы поможем в написании вашей работы!
5.3. Момент импульса
Моментом импульса (количества движения) L материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r − вектор, проведенный из точки О в точку А ; P = m V r − импульс матери-
P r относительно точки О.
Моментом импульса относительно неподвижной оси z называется ска-
гда момент импульса отдельной частицы относительно оси z можно представить в виде
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно этой оси на угловую скорость.
Для однородного тела, симметричного относительно оси вращения, момент импульса относительно любой точки этой оси определяется по формуле:
5.4. Уравнение динамики вращательного движения твердого тела
Наиболее общая форма записи основного уравнения динамики вращательного движения твердого тела имеет вид
— момент импульса тела относительно неподвижной точки О;
марный момент всех сил, действующих на тело, определенный относительно той же точки О.
где J – момент инерции тела относительно оси z ; ε z
— проекция углового уско-
5.5. Закон сохранения момента импульса
Согласно уравнению (5.2), момент импульса системы материальных точек (тела) может изменяться под действием момента всех внешних сил. Отсюда следует важный вывод – закон сохранения момента импульса: момент импуль-
са замкнутой системы частиц относительно неподвижной точки О остается постоянным во времени.
Примеры, демонстрирующие применение уравнения динамики вращательного движения твердого тела и закона сохранения момента импульса, приведены в приложении к описанию лабораторной работы № 1-8.
Кинетическая энергия вращательного движения определяется по формуле
ГЛАВА 6 Молекулярно – кинетическая теория идеальных газов
Молекулярная физика – раздел курса общей физики, в котором изучаются строение и свойства вещества, исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.
6.1. Опытные законы идеального газа
· собственный объем молекул газа много меньше объема сосуда;
· между молекулами газа отсутствуют силы взаимодействия;
· столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Многие реальные газы (например, водород, гелий, неон, азот, кислород, воздух и др.) в условиях близких к нормальным близки по своим свойствам к
идеальному газу. За нормальные условия принято считать давление P =1,013·10 5 Па, что соответствует 1 атм или 762 мм ртутного столба, и температуру окружающей среды t =0 0 С. Кроме того, если внести поправки на объем молекул и молекулярные силы, от теории идеального газа можно перейти к теории реального газа.
Опытным путем до создания молекулярно-кинетической теории был открыт целый ряд законов, которым удовлетворяет идеальный газ.
где V 0 – объем газа при нулевой температуре
Закон Шарля: давление данной массы газа ( m = const ) при постоянном объеме ( V = const ) изменяется линейно с температурой:
законы Гей-Люссака и Шарля можно переписать в виде
Закон Бойля – Мариотта: для данной массы газа ( m = const ) при постоянной температуре ( T = const ) произведение давления газа на его объем есть величина постоянная:
Закон Авогадро: моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы. При нормальных
V m = 22,41 10 − 3 м 3 / моль = 22,41 л/моль.
Моль – единица количества вещества в СИ. В одном моле содержится столько атомов (молекул, ионов), сколько атомов содержится в 12 г изотопа
Из сказанного выше следует, что в одном моле различных веществ содержится одно и то же число молекул, которое называется числом Авогадро :
Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
4.1. Динамика поступательного движения твердого тела.
Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.
Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс
Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.
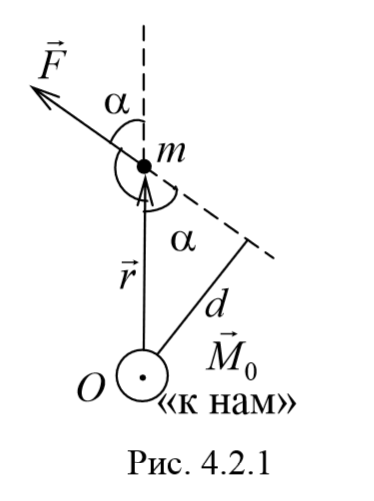
4.2. Момент импульса. Момент силы.
Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра
Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.
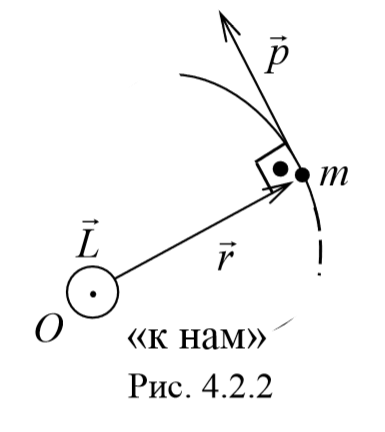
Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:
Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра
Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.
Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.
Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы
4.3. Основное уравнение динамики вращательного движения относительно точки.
Запишем уравнения движения частиц:
Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим
Преобразуем данные уравнения
Сложим эти уравнения и получим
В последнем уравнении:
Таким образом, выражение (4.3.6) можно записать в виде
4.4. Закон сохранения момента импульса.
закон сохранения момента импульса.
Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.
Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.
Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.
4.5. Момент инерции.
Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:
Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.
Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:
где R − расстояние от элементарной массы dm до оси вращения.
4.6. Теорема Штейнера. Правило аддитивности
Существуют два свойства момента инерции:
1) Теорема Штейнера: момент инерции тела Iz относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:
2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси: