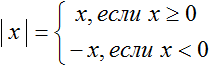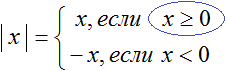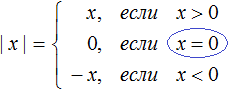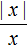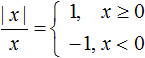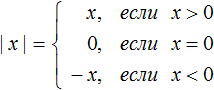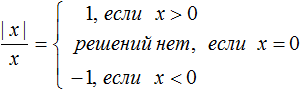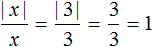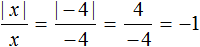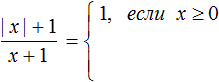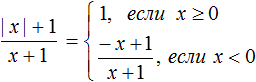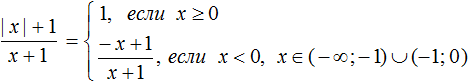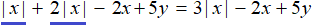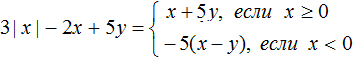что такое модуль в геометрии

Что такое модуль действительного числа

В данной публикации мы рассмотрим определение, геометрическую интерпретацию, график функции и примеры модуля положительного/отрицательного числа и нуля.

Определение модуля числа

Модуль действительного числа (иногда называется абсолютной величиной) – это величина, равная ему же, если число положительное или равная противоположному, если оно отрицательное.

Модуль числа a обозначается вертикальными черточками с обеих сторон от него – |a|.

Противоположное число отличается от исходного знаком. Например, для числа 5 противоположным является -5. При этом ноль является противоположным самому себе, т.е.

Геометрическая интерпретация модуля

Модуль числа a – это расстояние от начала координат (O) до точки A на координатной оси, которая соответствует числу a, т.е.

График функции с модулем

График четной функции y = |х| выглядит следующим образом:

Чему равняются следующие модули |3|, |-7|, |12,4| и |-0,87|.

Решение:
Согласно приведенному выше определению:

Источник

Обобщённое понятие модуля числа

В данном уроке мы рассмотрим понятие модуля числа более подробно.

Что такое модуль?

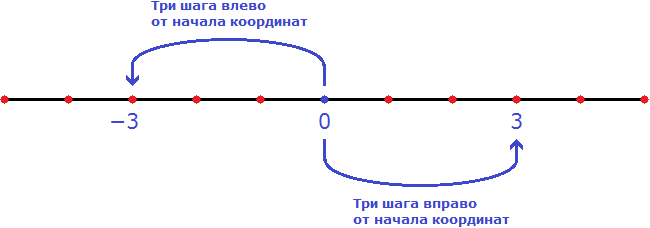
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3

Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:

Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:

Где x₁ и x₂ — числа на координатной прямой.

Например, отметим на координатной прямой числа 2 и 5.

Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:

Видим, что расстояние от числа 2 до числа 5 равно трём шагам:

Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3

То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:

Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:

Это равенство можно прочитать так: Расстояние от x₁ до x₂ равно расстоянию от x₂ до x₁.

Раскрытие модуля

Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.

Правило раскрытия модуля выглядит так:

В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.

Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x

Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5

В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0

Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.

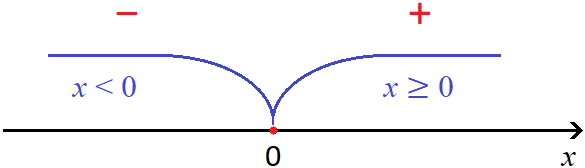
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:

А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:

Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,

Корень из числа 4 равен 2. Тогда модуль примет вид

x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x |√4 − 6| = |2 − 6| = |−4| = −(−4) = 4

На практике обычно рассуждают так:

«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».

Примеры:

|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0

Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:

В данном случае выполняется условие x=0, ведь 0 = 0

Пример 5. Раскрыть модуль в выражении |x|+ 3

Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.

Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:

Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 |x| + 3 = 3 − x = 3 − (−6) = 9

Пример 6. Раскрыть модуль в выражении x +|x + 3|

Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11

Найдём значение выражения x +|x + 3| при x=−3.

Пример 3. Раскрыть модуль в выражении

Как и прежде используем правило раскрытия модуля:

В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0

Перепишем решение так:

Пример 4. Раскрыть модуль в выражении

Но надо учитывать, что при x = − 1 знаменатель выражения 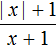обращается в ноль. Поэтому второе условие x следует дополнить записью о том, какие значения может принимать x

Преобразование выражений с модулями

Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.

Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.

Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.

Решение

Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:

В итоге имеем следующее решение:

Пример 2. Раскрыть модуль в выражении: −|x|

Решение

Источник

Модуль числа

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Записывайся на занятия по математике для учеников с 1 по 11 классы.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

Оно равно a при а > 0 и −а, при а

Модуль комплексного числа

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Модуль вещественных чисел

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Закрепим свойства модуля числа, которые мы рассмотрели выше:

Источник