что такое моделирующий алгоритм
Моделирующий алгоритм.
Математическое описание служит исходным материалом для создания алгоритма, моделирующего исследуемый объект. Задачей моделирующего алгоритма является решение системы уравнений математического описания, что позволяет находить внутренние параметры математической модели при заданной совокупности внешних параметров. В процессе математического моделирования иногда встречаются задачи, в которых фиксируют определенные значения ряда внутренних параметров и требуется определить набор внешних параметров, обеспечивающих получение фиксированных внутренних параметров. Такие задачи возникают, например, при решении задач управления, когда для заданного режима работы объекта необходимо найти значения управляющих воздействий, обеспечивающих заданный режим функционирования объекта. Эта проблема не так проста, как кажется на первый взгляд. По существу это обратная задача, так как нужно искать набор управляющих воздействий, соответствующих заданному режиму.
Для решения систем уравнений математической модели в настоящее время имеются пакеты программ для решения дифференциальных уравнений как обыкновенных, так и в частных производных. В частности, такие возможности предоставляют известные системы Mathlab и Mathcad. Созданы также специализированные программные комплексы Aspen, HYSYS и ReactOp для решения математических моделей технологических объектов. Так что выбор моделирующего алгоритма в настоящее время сводится к четкой формулировке задачи, выбору внутренних и внешних переменных и соответствующего программного пакета.
2. Общие принципы и этапы построения математических моделей систем.
Моделирующий алгоритм. Имитационная модель



Имитационный характер исследования предполагает наличие логико или логико-математических моделей, описываемых изучаемый процесс (систему).
Логико-математическая модель сложной системы может быть как алгоритмической, так и неалгоритмической (например, система дифференциальных уравнений преобразуется в алгоритмическую с использованием численного метода интегрирования, при этом свойства модели меняются и это надо учитывать).
Чтобы быть машинно-реализуемой, на основе логико-математической модели сложной системы строится моделирующий алгоритм, который описывает структуру и логику взаимодействия элементов в системе.
2.4 Проблемы стратегического и тактического планирования имитационного эксперимента. Направленный вычислительный эксперимент на имитационной модели
В начале этой лекции мы в общем виде дали понятие метода имитационного моделирования. Мы определили имитационное моделирование как экспериментальный метод исследования реальной системы по ее имитационной модели.
Рассмотрим особенности этого экспериментального метода. Кстати, слова «simulation», «эксперимент», «имитация» одного плана. Экспериментальная природа имитации также предопределила происхождение названия метода. Итак, цель любого исследования состоит в том, чтобы узнать как можно больше об изучаемой системе, собрать и проанализировать информацию, необходимую для принятия решения. Суть исследования реальной системы по ее имитационной модели состоит в получении (сборе) данных о функционировании системы в результате проведения эксперимента на имитационной модели (см. лекцию 1: имитационный метод исследования).
Для пояснения рассмотрим 2 случая: детерминированный случай; стохастический случай.
Итак, в случае со стохастической системой необходимо осуществлять сбор и оценивание статистических данных на выходе имитационной модели,- для этого проводить серию прогонов и статистическую обработку результатов моделирования.
Детерминированный случай. В этом случае достаточно провести один прогон, по определенным операционным правилам при конкретном наборе параметров.
Теперь представим, что целями моделирования являются: исследование системы при различных условиях, оценка альтернатив, нахождение зависимость выхода модели от ряда параметров и, наконец, поиск некоторого оптимального вариант. В этих случаях исследователь может проникнуть в особенности функционирования моделируемой системы, изменяя значения параметров на входе модели, при этом выполняя многочисленные машинные прогоны имитационной модели.
Таким образом, проведение экспериментов с моделью на ЭВМ заключается в проведении многократных машинных прогонов с целью сбора, накопления и последующей обработки данных о функционировании системы. Имитационное моделирование позволяет исследовать модель реальной системы, чтобы изучать ее поведение путем многократных прогонов на ЭВМ при различных условиях функционирования реальной системы.
Здесь возникают следующие проблемы: как собрать эти данные, провести серию прогонов, как организовать целенаправленное экспериментальное исследование. Выходных данных, полученных в результате такого экспериментирования, может оказаться очень много. Как их обработать? Обработка и изучение их может превратиться в самостоятельную проблему, намного сложнее задачи статистического оценивания.
В имитационном моделировании важным вопросом является не только проведение, но и планирование имитационного эксперимента в соответствии с поставленной целью исследования.
Эта проблема получила название стратегического планирования
имитационного исследования. Для ее решения используются методы регрессионного анализа, планирования эксперимента и др., которые подробно будут рассматриваться в лекции 7.
Наряду с понятием стратегического существует понятие тактического планирования,которое связано с определением способов проведения имитационных прогонов, намеченных планом эксперимента: как провести каждый прогон в рамках составленного плана эксперимента. Здесь решаются задачи: определение длительности прогона, оценка точности результатов моделирования и др.
Такие имитационные эксперименты с имитационной моделью будем называть направленными вычислительными экспериментами.
Имитационный эксперимент, содержание которого определяется предварительно проведенным аналитическим исследованием (т.е. являющимся составной частью вычислительного эксперимента) и результаты которого достоверны и математически обоснованы, назовем направленным вычислительным экспериментом.
В лекции 7 мы детально рассмотрим практические вопросы организации и проведения направленных вычислительных экспериментов на имитационной модели.
Лекция 32.
Общие принципы построения
моделирующих алгоритмов
При реализации моделирующих алгоритмов на цифровых машинах есть определенные общие закономерности, которые мы обсудим в данной лекции.
Основная проблема при составлении алгоритмов на машине с последовательной обработкой процессов состоит в том, что при моделировании необходимо отслеживать множество процессов, которые в реальном времени происходят параллельно. В связи с этим алгоритмы моделирования имеют свои особенности:
В настоящий момент известны четыре основных принципа регламентации событий.
Рассмотрим на примерах, как реализуется в моделирующих алгоритмах каждый принцип по отдельности.
Принцип Δt
Особенности реализации принципа Δt
Это наиболее универсальный из рассматриваемых принципов, так как применяется для очень широкого класса систем. Он же является наиболее простым в реализации, поскольку принцип Δt совпадает с пониманием человека о времени, как о последовательном явлении, текущем с постоянным темпом.
Однако это самый неэкономичный принцип, поскольку вся система анализируется моделирующим алгоритмом на каждом такте, даже если в ней не происходит никаких изменений.
| |
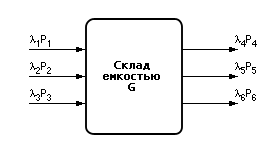
| Рис. 32.1. Схема моделируемой производственной системы (пример) |
Алгоритм построим таким образом, чтобы вычислить вероятности событий возникновения дефицита Pд и переполнения Pп на складе.
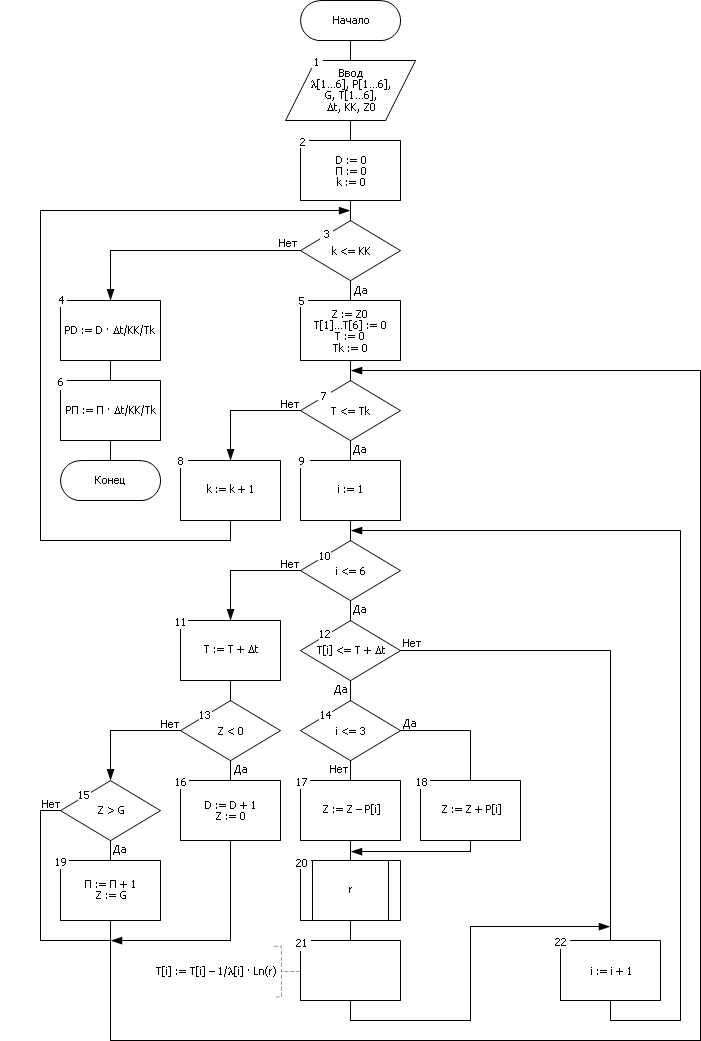
Для накопления надежной статистики эксперимент повторяется KK раз. За количеством экспериментов следит счетчик экспериментов k (блоки 2, 3, 8). Каждый эксперимент длится от 0 до Tk момента времени (блоки 5, 7). Счетчик времени t отсчитывает время от 0 до Tk с дискретностью Δt (блок 11).
Заметим, что поскольку на складе в реальности не может быть изделий меньше нуля, то значение Z в момент обнаружения этого факта должно быть возвращено на ближайшую границу, то есть: Z := 0 (блок 16). Тоже самое касается ситуации переполнения ( Z := G ) (блок 19).
| |
| Рис. 32.2. Блок-схема алгоритма, реализованного по принципу Δt. Пример моделирование производственного склада |
Принцип особых состояний
Назовем состояние, в котором обычно находится система, обычным состоянием. Такие состояния интереса не представляют, хотя занимают большую часть времени.
Особые состояния это такие состояния в изолированные моменты времени, в которых характеристики системы изменяются скачкообразно. Для изменения состояния системы нужна определенная причина, например, приход очередного входного сигнала. Ясно, что с точки зрения моделирования интерес представляет именно изменение характеристик системы, то есть принцип требует от нас отслеживать моменты перехода системы из одного особого состояния в другое.
Все это существенно экономит время моделирования.
| |
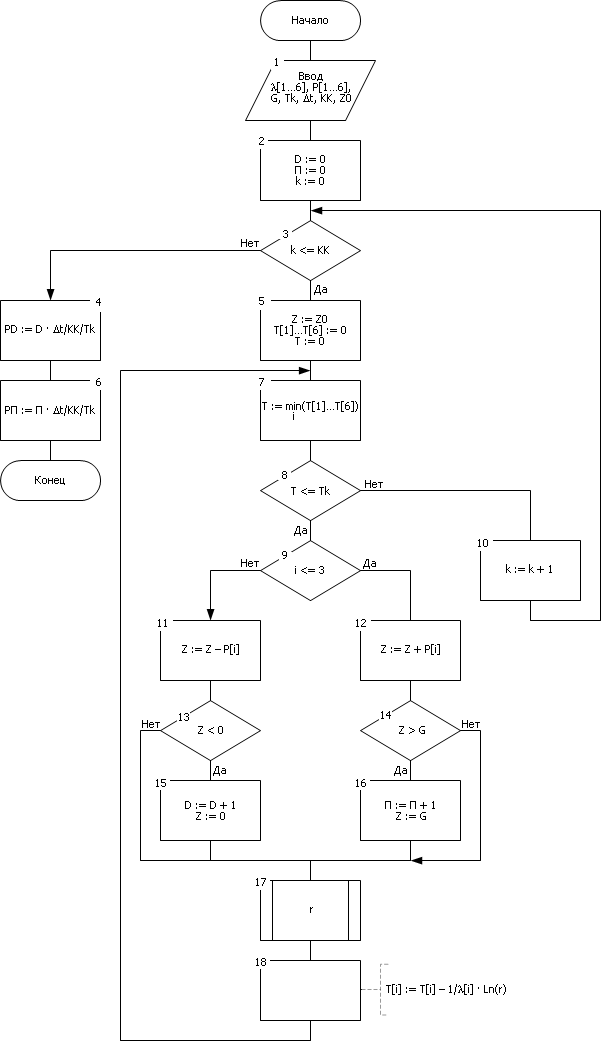
| Рис. 32.3. Блок-схема алгоритма, реализованного по принципу особых состояний. Пример моделирование производственного склада |
Принцип последовательной проводки заявок
Принцип состоит в том, что каждая заявка отслеживается от момента поступления ее в систему до момента ее выхода из системы. И только потом рассматривается следующая заявка.
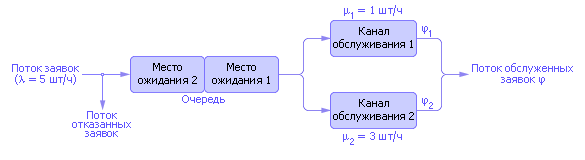
Рассмотрим работу алгоритма на примере двухканальной системы массового обслуживания заявок с двумя местами в общей очереди с дисциплиной FIFO и отказами при переполнении очереди (см. рис. 32.4 ), см. также лекцию 30.
| |
| Рис. 32.4. Схема системы массового обслуживания с двумя каналами и ограниченной очередью |
Обозначим: λ интенсивность прихода заявки; μi интенсивность обслуживания заявки.
Построим алгоритм, определяющий вероятности обслуживания заявок и отказа заявок, а также пропускную способность системы.
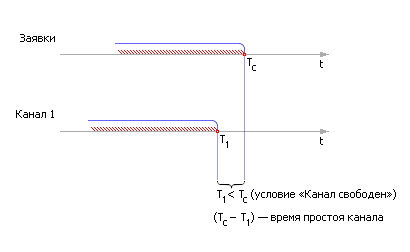
Чтобы понять работу алгоритма, представьте себе для наглядности параллельные линейки оси времени для каждого из мест, в которых может оказаться заявка в процессе обслуживания так, как мы это делали ранее (см. лекцию 30).
| |
| Рис. 32.5. Механизм определения освобождения канала (иллюстрация) |
Аналогично обработка происходит и во втором канале, если заявка попадет именно туда (блок 14).
Особенность обработки заявки в очереди состоит в том, что первое место в очереди освобождается, когда освобождается место в одном из каналов, конечно, заявка уходит туда, где место освобождается раньше (блоки 5, 6). Второе место в очереди освобождается одновременно с первым, так как заявка в очереди передвигается на первое освободившееся место (блок 12).
Далее алгоритм генерирует в цикле следующую заявку (блоки 3, 16). Остановка моделирования происходит тогда, когда каждая линейка будет заполнена до момента Tk (блок 16). После этого происходит обработка статистических результатов, накопленных в счетчиках (блок 17). Вероятность оценивается частостью появления события, которая вычисляется как отношение количества появившихся событий к количеству возможных таких появлений.
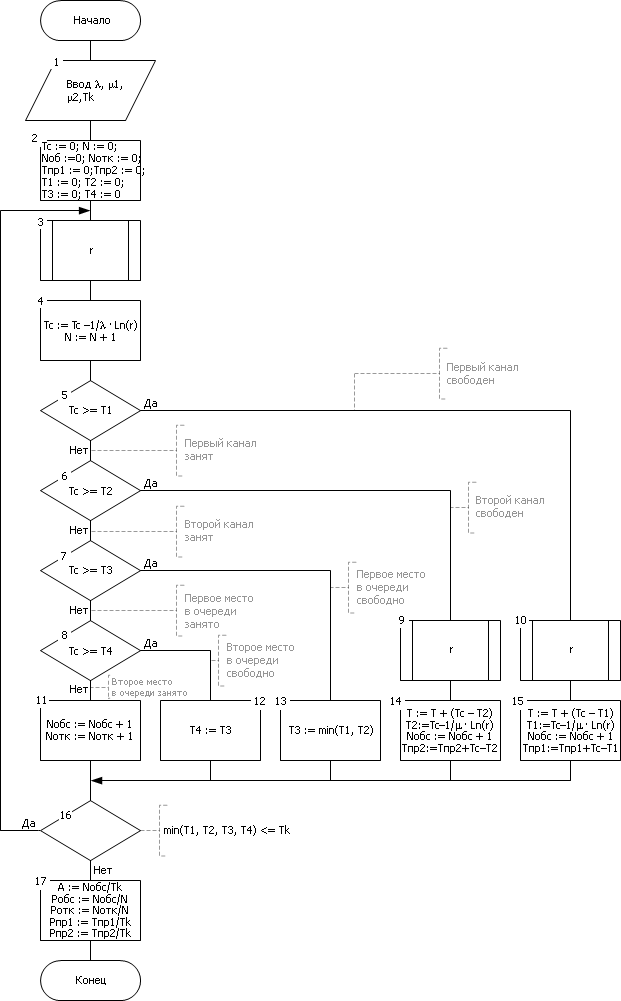
| |
| Рис. 32.6. Блок-схема алгоритма, реализованного по принципу последовательной проводки заявок. Пример моделирование системы массового обслуживания |
И, конечно, надо помнить, что чем больше время моделирования, тем точнее будет вычисленный результат.
Необходимо внимательно следить, чтобы все искомые переменные вошли в интервал объявленной точности, только тогда можно прекратить моделирование и быть уверенным в результате.
Для повышения эффективности алгоритма (уменьшения времени его работы) можно отброс ить нехарактерную часть реализации обычно это начальный участок работы системы, «выход ее на режим».
Заметим также, что не важно, имеем ли мы дело с одной длинной реализацией или с большим количеством коротких реализаций (у которых, конечно, вырезан участок «выход на режим»), в сумме дающих реализацию такой же длины статистический результат будет тем же. Это рассуждение устанавливает равенство усреднений по ансамблю реализаций усреднениям по времени.
Примечание. На практике обычно применяют комбинации всех трех методов.
Объектный принцип моделирования
Как правило, алгоритмы, спроектированные по первым трем принципам, плохо модернизируются. А производственная ситуация часто меняется и требует соответствующих моделей для нахождения рациональных решений в процессе управления.
Таким образом, возникла необходимость в приемах моделирования, обеспечивающих независимость составления моделей элементов сложной системы от изменения задачи или структуры производства. Такой подход моделирования отдельных объектов независимо друг от друга позволяет собирать сколь угодно сложные системы без изменения их составляющих. Принцип объектного моделирования обеспечивает модернизацию сложных систем, удлиняя жизненный цикл АСУ.
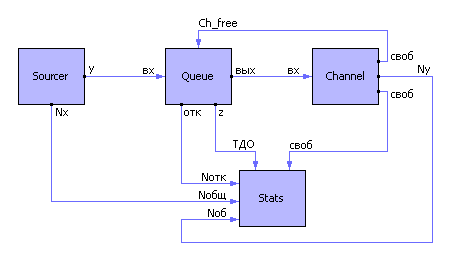
| |
| Рис. 32.7. Схема реализации объектно-ориентированного моделирования (на примере СМО) |
1. Источник заявок (Sourcer) генерирует последовательность случайных событий.
|