что такое моделирование как научный метод
Естествознание. 10 класс
Конспект урока
Естествознание, 10 класс
Урок 8. Моделирование в науке
Перечень вопросов, рассматриваемых в теме:
Модель (франц. modele, от лат. modulus мера, образец, норма) — это форма отображения определённого фрагмента действительности (предмета, явления, процесса, ситуации), который содержит существенные свойства моделируемого объекта и может быть представлен в абстрактной (мысленной или знаковой) или материальной (предметной) форме.
Моделирование – метод теоретического познания, состоящий в исследовании каких-либо явлений, процессов или систем путем построения и изучения их моделей; использование моделей для определения поведения и характеристик реальных систем.
Математическая модель – модели, построенные с использованием математических понятий и инструментария (формул, графиков, систем уравнений и т.д.)
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
Открытые электронные ресурсы по теме урока :
Теоретический материал для самостоятельного изучения
Реальные объекты исследования не всегда доступны для исследователя или в их функционирование нельзя вмешиваться. В этом случает можно заменить «оригинал» соответствующим аналогом (моделями), пользуясь которым можно провести эксперимент, изучать его поведение при изменениях параметров внешней и внутренней среды. В воспроизведении свойств объекта изучения на специально устроенном его аналоге-модели заключается суть процесса моделирование. Сама модель — это всегда упрощенное отражение объекта, копия реального объекта, обладающая его основными характеристиками и способная имитировать его поведение.
Модели могут быть реальными (материальными), например, модели самолетов, макеты зданий, фотографии, протезы, куклы и т.п., а также теоретическими (идеальными или абстрактными), создаваемые средствами языка (как естественного человеческого языка, так и специальных языков, например, языком математики. В этом случае мы имеем математическую модель, которая описывает взаимосвязи в изучаемой системе).
Математическое моделирование – инструмент познания, изучения и исследования сложных систем. Эти системы сложны потому, что либо состоят из большого числа структурных компонентов, либо находятся под влиянием большего числа внешних факторов. В этом случае ученые создают модели – упрощенные копии систем, отражающие их структуру и функциональные взаимосвязи. В логике исследования под особым вниманием находятся лишь некоторые компоненты системы и ее взаимосвязи. Математические модели могут быть представлены в виде математических формул, систем уравнений, графиков и т.д. Например, системы дифференциальных уравнений в модели Лотки-Вольтерра, изучающей системы «паразит-хозяин» и «хищник-жертва» или графический образ экологических пирамид (масс, энергий) и др.
Выделяют три функции моделирования:
Познавательная функция заключается в том, что за счет абстрагирования модели позволяют достаточно просто объяснить наблюдаемые на практике явления и процессы (другими словами, они дают ответ на вопрос «почему мир устроен так»).
Прогностическая функция моделирования отражает его возможность предсказывать будущие свойства и состояния моделируемых систем, то есть отвечать на вопрос «что будет?».
Нормативная функция моделирования заключается в получении ответа на вопрос «как должно быть?» – если, помимо состояния системы, заданы критерии оценки ее состояния, то возможно не только описать существующую систему, но и построить ее нормативный образ – желательный с точки зрения субъекта, интересы и предпочтения которого отражены используемыми критериями.
Примеры моделей различных типов в естественных науках
Моделирование как метод научного исследования
Вы будете перенаправлены на Автор24
Сущность и целевое назначение моделирования
Моделирование – это метод, применяемый для изучения разного рода процессов и явлений, разработки вариаций принятия управленческих решений.
Моделирование осуществляется на основе построения моделей, которые являются заменителями реальных объектов, процессов и явлений. Методика предполагает описание структурного устройства, изучаемого объекта, его свойств и параметров, процесса его функционирования во времени и пространстве, а также характеристики особенностей развития.
Построение моделей позволяет воспроизвести связи, характеристики, особенности функционирования, тенденции и динамику развития, исследуемых объектов, систем, явлений и процессов, проанализировать их текущее состояние, спланировать и составить прогноз последующего развития и принять рациональное решение, обосновать его и эффективно воплотить на практике.
Методика моделирования хороша тем, что она обеспечивает системный и целостный подход к исследованию, что положительно сказывается на разработке методов целостного управленческого воздействия, позволяет получить новые знания и усовершенствовать параметры, исследуемых объектов или процессов.
В процессе моделирования предполагается создание образцов, как внешнего строения объектов, например, каких-то предметов познания, так и их функциональной роли или логического назначения.
Моделирование осуществляется в двух основных формах:
Рисунок 1. Моделирование. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Как и любой процесс, включенный в систему образования, моделирование начинается с постановки цели разработки модели. Она определяет дальнейшее содержание моделирования, выбор форм, методов и средств организации данного процесса. Структура модели, ее составные компоненты определяются целевым назначением той или иной модели.
Целевым назначением моделирования может быть:
Для одного и того же объекта изучения может быть построено несколько моделей. Это объясняется тем, что в одной модели оптимально можно воплотить лишь определенные свойства или их группу, которые являются наиболее важными для данного объекта или процесса.
Классификация моделей, применяемых в педагогике
Модели научного исследования могут быть классифицированы по различным основаниям. Если модель выбирается, исходя из ее целевого назначения, то она может быть:
Существует и иная классификация моделей, определяющая их целевое назначение:
В педагогике особенно актуальным является применение двух видов моделей:
Функциональное назначение моделирования
Процесс моделирования выполняет следующие основные функции:
Моделирование как метод научного исследования — Сущность метода моделирования
Ежедневно каждый человек сталкивается с множеством моделей каких-то предметов. Даже в детстве ребенок играет с кубиками – моделями геометрических фигур. Но термин «модель» употребляется не только по отношению к предметам. А также к процессам и явлениям. К примеру, привычки человека, его повадки, поведение, речь – это все модель поведения. Даже жизненный опыт человека, его представления о мире является примером модели. Таким образом, модель — это упрощенное представление о реальном объекте, процессе или явлении.
Сложно представить человеческую жизнедеятельность без использования различного рода моделей. Однако особую важность модель и процесс ее создания, изучения и применения – моделирование, имеют для науки. Моделирование является неотъемлемым инструментом в таких разделах науки как физика, химия, биология, кибернетика, не говоря уже о многих технических науках. Именно поэтому моделирование как способ научных исследований вызывает такой интерес философии и методологии познания.
Целью данной работы является анализ сущности методов моделирования и метода математической гипотезы. В работе будут рассмотрены основные принципы и концепции обоих методов, перечислены основные цели моделирования, классификация моделей. А также рассмотрены принципы отбора математических гипотез. Главной задачей работы является написание сравнительной характеристики данных методов на основе изученного материала.
Сущность метода моделирования
Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХв. Однако методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться роль моделирования как универсального метода научного познания.
Термин «модель» широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Рассмотрим только такие «модели», которые являются инструментами получения знаний.
Модель — это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.[2] Под моделированием понимается процесс построения, изучения и применения моделей. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез.
В широком смысле моделирование — многоплановый метод исследования, один из путей познания. Оно предполагает исследование реально существующих предметов, явлений, социальных процессов, органических и неорганических систем. А это значит, что сферы применения моделирования, по существу, неограниченны. Ими охватываются все процессы. Но это вовсе не означает, что моделирование является единственным и исчерпывающим методом познания, хотя моделирование присуще всякому познавательному процессу.
Общество не может разумно развиваться, не анализируя себя, различные стороны своей деятельности, не контролируя себя, не заглядывая вперед. Но для того чтобы этот анализ был эффективным, он должен опираться на точные, объективные данные, т.е. необходима информационная база, социальная информация. Совокупность проблем, поддающаяся количественному анализу, может быть формализована, выражена языком цифр и обработана на ЭВМ с помощью математического моделирования. Но далеко не все процессы общества поддаются количественному измерению и контролю. Социальные отношения отличаются исключительной сложностью, в них взаимодействуют самые различные факторы, взаимовлияние которых друг на друга неоднозначно, вариативно; причинно-следственные связи, их интенсивность и характер подвижны и неопределенны. К тому же следует учитывать, что все социальные процессы осуществляются людьми, а поступки, мысли, чувства людей не могут иметь числового отображения.
Отсюда — объективно необходимыми становятся различные методы анализа качественного содержания процессов в социальной сфере. А значит, необходимы и самые различные модели, функциями которых являются:
Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания.
Требования к модели
Целесообразно выделить две группы требований. Во-первых, модель должна быть более простой, более удобной, давать новую информацию об объекте, способствовать усовершенствованию самого объекта. Во-вторых, модель должна способствовать определению или улучшению характеристик объекта, рационализации способов построения его, управлению или познанию объекта. Следовательно, правомерно при разработке модели говорить об ее подобии объекту-оригиналу, при котором, с одной стороны, соблюдается жесткая целенаправленность, увязка ее параметров с ожидаемыми результатами, а с другой — обеспечивается достаточная «свобода» модели, для того чтобы она была способной к преобразованию в зависимости от конкретных условий и обстоятельств, могла быть альтернативной, иметь в запасе наибольшее число вариантов.
В целом модель должна соответствовать следующим требованиям. Модель должна:
Параметры оценки моделей могут быть различными. Один из них — прогрессивность модели, означающая, насколько она по целому ряду моментов является лидирующей. Определение качества модели не такая простая задача, особенно когда речь идет о моделях социальной сферы. Прогрессивность модели определяется характеристиками свойств модели, применимой в той или иной сфере в зависимости от целей и задач исследователей. В качестве главных критериев выступают: новизна отражения (интуитивное отражение, качественное описание, наглядная имитация, системное воспроизведение), распространенность, уровень разработанности. Уровень творческого решения с помощью модели означает степень выполнения гносеологической (познавательной, объяснительной) и эвристической (прогностической, творческой) функций. Последовательность нарастания этих возможностей, т.е. творческого решения, следующая:
Не менее важным является рассмотрение структуры моделей. В структуру моделей входят три основных компонента: совокупность направлений развития объекта познания, побудительные силы развития, факторы внешних воздействий. При исследовании важно зафиксировать степень реализованного воздействия всех основных компонентов на предыдущем этапе познания объекта, что может быть осуществлено при ретроспективном анализе.
Классификация моделей
Признаки классификаций моделей:
1) по области использования;
2) по фактору времени;
3) по отрасли знаний;
4) по форме представления
1) Классификация моделей по области использования:
Учебные модели – используются при обучении. Это могут быть наглядные пособия, различные тренажеры, обучающие программы.
Опытные модели – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик.
Например, модель корабля исследуется в бассейне для изучения устойчивости судна при качке, модель автомобиля «продувается» в аэродинамической трубе с целью исследования обтекаемости кузова, модель сооружения используется для привязки здания к конкретной местности и т.д.
Научно – технические модели — создаются для исследования процессов и явлений. К таким моделям можно отнести, например, прибор для получения грозового электрического разряда или стенд для проверки телевизоров.
Игровые модели – это военные, экономические, спортивные, деловые игры. Эти модели как бы репетируют поведение объекта в различных ситуациях, проигрывая их с учетом возможной реакции со стороны конкурента, союзника или противника. С помощью игровых моделей можно оказывать психологическую помощь больным, разрешать конфликтные ситуации.
Имитационные модели непросто отражают реальность с той или иной степенью точности, а имитируют ее. Эксперименты с моделей проводят при разных исходных данных. По результатам исследования делаются выводы. Такой метод подбора правильного решения получил название (метод проб и ошибок). Например, для выявления побочных действий лекарственных препаратов их испытывают в серии опытов над животными.
2) Классификация моделей по фактору времени:
Статические – модели, описывающие состояние системы в определенный момент времени (единовременный срез информации по данному объекту). Например, обследование учащихся в стоматологической поликлинике дает состояние их зубов в данный момент времени: соотношение молочных и постоянных, наличие пломб, дефектов и т.п.
Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени). Примеры: описание движения тел, развития организмов, процесс химических реакций.
При строительстве дома рассчитывают прочность его фундамента, стен, балок и устойчивость их к постоянной нагрузке. Это статическая модель здания. Но надо так же обеспечить противодействие ветрам, движению грунтовых вод, сейсмическим колебаниям и другим, изменяющимся во времени факторам. Эти вопросы можно решить с помощью динамических моделей.
Таким образом, один и тот же объект можно охарактеризовать и статической и динамической моделью.
3) Классификация моделей по отрасли знаний
— это классификация по отрасли деятельности человека: математические, биологические, химические, социальные, экономические, исторические и тд.
4) Классификация моделей по форме представления:
Материальные – это предметные (физические) модели. Они всегда имеют реальное воплощение. Отражают внешнее свойство и внутреннее устройство исходных объектов, суть процессов и явлений объекта-оригинала. Это экспериментальный метод познания окружающей среды. Примеры: детские игрушки, скелет человека, чучело, макет солнечной системы, школьные пособия, физические и химические опыты
Абстрактные (нематериальные) – не имеют реального воплощения. Их основу составляет информация. Это теоретический метод познания окружающей среды. По признаку реализации они бывают: мысленные и вербальные; информационные
Мысленные модели формируются в воображении человека в результате раздумий, умозаключений, иногда в виде некоторого образа. Это модель способствует сознательной деятельности человека. Примером мысленной модели является модель поведения при переходе через дорогу. Человек анализирует ситуацию на дороге (какой сигнал подает светофор, как далеко находятся машины, с какой скоростью они движутся и т.п.) и вырабатывается модель поведения. Если ситуация смоделирована правильно, то переход будет безопасным, если нет, то может произойти дорожно-транспортное происшествие.
Вербальные (от лат. verbalis – устный) – мысленные модели, выраженные в разговорной форме. Используется для передачи мыслей.
Чтобы информацию можно было использовать для обработки на компьютере, необходимо выразить ее при помощи системы знаков, т.е. формализовать. Правила формализации должны быть известны и понятны тому, кто будет создавать и использовать модель. Поэтому наряду с мысленными и вербальными моделями используют более строгие – информационные модели.
Информационные модели – целенаправленно отобранная информация об объекте, которая отражает наиболее существенные для исследователя свойства этого объекта.
Типы информационных моделей
Табличные – объекты и их свойства представлены в виде списка, а их значения размещаются в ячейках прямоугольной формы. Перечень однотипных объектов размещен в первом столбце (или строке), а значения их свойств размещаются в следующих столбцах (или строках)
Иерархические – объекты распределены по уровням. Каждый элемент высокого уровня состоит из элементов нижнего уровня, а элемент нижнего уровня может входить в состав только одного элемента более высокого уровня
Сетевые – применяют для отражения систем, в которых связи между элементами имеют сложную структуру
По степени формализации информационные модели бывают образно-знаковые и знаковые.
Ярким примером образно-знаковой модели является географическая карта. Цвет и форма материков, океанов, гор, изображенных на карте, сразу подключает образное мышление. По цвету на карте сразу можно оценить рельеф. Например, с голубым цветом у человека ассоциируется вода, с зеленым цветущий луг, равнина. Карта изобилует условными обозначениями. Зная этот язык, человек может получить достоверную информацию об интересующем его объекте. Информационная модель в этом случае будет результатом осмысления сведений, полученных при помощи органов чувств и информации, закодированной в виде условных изображений.
То же можно сказать о живописи. Неискушенный зритель воспримет картину душой в виде образной модели. Но существуют некоторые художественные языки, соответствующие различным живописным жанрам и школам: сочетание цветов, характер мазка, способы передачи воздуха, объема и т. д. Человеку, знающему эти условности, легче разобраться в том, что имел в виду художник, особенно если произведение не относится к реализму. При этом общее восприятие картины (информационная модель) станет результатом осмысления информации как в образной, так и в знаковой формах.
Еще один пример такой модели — фотография. Фотоаппарат позволяет получить изображение оригинала. Обычно фотография дает нам довольно точное представление о внешнем облике человека. Существуют некоторые признаки (высота лба, посадка глаз форма подбородка), по которым специалисты могут определить характер человека, его склонность к тем или иным поступкам. Этот специальный язык формируется из сведений, накопленных в области физиогномики и собственного опыта. Знающие врачи, взглянув на фото незнакомого человека, увидят признаки некоторых заболеваний. Задавшись разными целями, по одной и той же фотографии можно получить различные информационные модели. Они будут результатом обработки образной информации, полученной при разглядывании фотографии, и информации, сложившейся на основе знания специального профессионального языка.
По форме представления образно-знаковых моделей среди них можно выделить следующие группы:
• геометрические модели, отображающие внешний вид оригинала (рисунок, пиктограмма, чертеж, план, карта, объемное изображение);
• структурные модели, отражающие строение объектов и связи их параметров (таблица, граф, схема, диаграмма);
• словесные модели, зафиксированные (описанные) средствами естественного языка;
• алгоритмические модели, описывающие последовательность действий.
Знаковые модели можно разделить на следующие группы:
• математические модели, представленные математическими формулами, отображающими связь различных параметров объекта, системы или процесса;
• специальные модели, представленные на специальных языках (ноты, химические формулы и т. п.);
• алгоритмические модели, представляющие процесс в виде программы, записанной на специальном языке.
На странице курсовые работы по педагогике вы найдете много готовых тем для курсовых по предмету «Педагогика».
Читайте дополнительные лекции:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Моделирование как метод научного познания
1. Моделирование как метод научного познания.
Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХ в. Однако методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться роль моделирования как универсального метода научного познания.
Термин «модель» широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Рассмотрим только такие «модели», которые являются инструментами получения знаний.
Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания.
Необходимость использования метода моделирования определяется тем, что многие объекты (или проблемы, относящиеся к этим объектам) непосредственно исследовать или вовсе невозможно, или же это исследование требует много времени и средств.
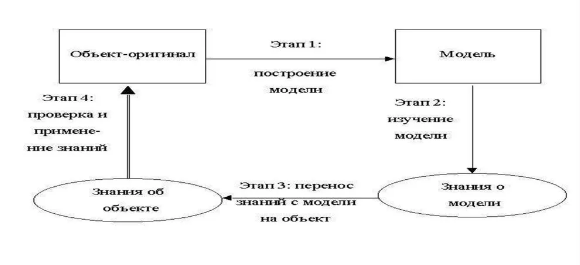
Процесс моделирования включает три элемента:
1) субъект (исследователь),
2) объект исследования,
3) модель, опосредствующую отношения познающего субъекта и познаваемого объекта.
Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от отражения других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.
На втором этапе процесса моделирования модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о ее «поведении». Конечным результатом этого этапа является множество знаний о модели R.
На третьем этапе осуществляется перенос знаний с модели на оригинал формирование множества знаний S об объекте. Этот процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели. Мы можем с достаточным основанием переносить какой-либо результат с модели на оригинал, если этот результат необходимо связан с признаками сходства оригинала и модели. Если же определенный результат модельного исследования связан с отличием модели от оригинала, то этот результат переносить неправомерно.
Четвертый этап практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.
Моделирование циклический процесс. Это означает, что за первым четырехэтапным циклом может последовать второй, третий и т.д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта и ошибками в построении модели, можно исправить в последующих циклах. В методологии моделирования, таким образом, заложены большие возможности саморазвития.
2. Особенности применения метода математического моделирования в экономике.
Проникновение математики в экономическую науку связано с преодолением значительных трудностей. В этом отчасти была «повинна» математика, развивающаяся на протяжении нескольких веков в основном в связи с потребностями физики и техники. Но главные причины лежат все же в природе экономических процессов, в специфике экономической науки.
Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием сложная система.
Сложность экономики иногда рассматривалась как обоснование невозможности ее моделирования, изучения средствами математики. Но такая точка зрения в принципе неверна. Моделировать можно объект любой природы и любой сложности. И как раз сложные объекты представляют наибольший интерес для моделирования; именно здесь моделирование может дать результаты, которые нельзя получить другими способами исследования.
Потенциальная возможность математического моделирования любых экономических объектов и процессов не означает, разумеется, ее успешной осуществимости при данном уровне экономических и математических знаний, имеющейся конкретной информации и вычислительной технике. И хотя нельзя указать абсолютные границы математической формализуемости экономических проблем, всегда будут существовать еще неформализованные проблемы, а также ситуации, где математическое моделирование недостаточно эффективно.
3. Особенности экономических наблюдений и измерений.
Уже длительное время главным тормозом практического применения математического моделирования в экономике является наполнение разработанных моделей конкретной и качественной информацией. Точность и полнота первичной информации, реальные возможности ее сбора и обработки во многом определяют выбор типов прикладных моделей. С другой стороны, исследования по моделированию экономики выдвигают новые требования к системе информации.
Методы экономических наблюдений и использования результатов этих наблюдений разрабатываются экономической статистикой. Поэтому стоит отметить только специфические проблемы экономических наблюдений, связанные с моделированием экономических процессов.
В экономике многие процессы являются массовыми; они характеризуются закономерностями, которые не обнаруживаются на основании лишь одного или нескольких наблюдений. Поэтому моделирование в экономике должно опираться на массовые наблюдения.
Другая проблема порождается динамичностью экономических процессов, изменчивостью их параметров и структурных отношений. Вследствие этого экономические процессы приходится постоянно держать под наблюдением, необходимо иметь устойчивый поток новых данных. Поскольку наблюдения за экономическими процессами и обработка эмпирических данных обычно занимают довольно много времени, то при построении математических моделей экономики требуется корректировать исходную информацию с учетом ее запаздывания.
Познание количественных отношений экономических процессов и явлений опирается на экономические измерения. Точность измерений в значительной степени предопределяет и точность конечных результатов количественного анализа посредством моделирования. Поэтому необходимым условием эффектного использования математического моделирования является совершенствование экономических измерителей. Применение математического моделирования заострило проблему измерений и количественных сопоставлений различных аспектов и явлений социально-экономического развития, достоверности и полноты получаемых данных, их защиты от намеренных и технических искажений.
4. Случайность и неопределенность в экономическом развитии.
Для методологии планирования экономики важное значение имеет понятие неопределенности экономического развития. В исследованиях по экономическому прогнозированию и планированию различают два типа неопределенности: «истинную», обусловленную свойствами экономических процессов, и «информационную», связанную с неполнотой и неточностью имеющейся информации об этих процессах. Истинную неопределенность нельзя смешивать с объективным существованием различных вариантов экономического развития и возможностью сознательного выбора среди них эффективных вариантов. Речь идет о принципиальной невозможности точного выбора единственного (оптимального) варианта.
В развитии экономики неопределенность вызывается двумя основными причинами. Во-первых, ход планируемых и управляемых процессов, а также внешние воздействия на эти процессы не могут быть точно предсказуемы из-за действия случайных факторов и ограниченности человеческого познания в каждый момент. Особенно характерно это для прогнозирования научно-технического прогресса, потребностей общества, экономического поведения. Во-вторых, общегосударственное планирование и управление не только не всеобъемлющи, но и не всесильны, а наличие множества самостоятельных экономических субъектов с особыми интересами не позволяет точно предвидеть результаты их взаимодействий. Неполнота и неточность информации об объективных процессах и экономическом поведении усиливают истинную неопределенность.
На первых этапах исследований по моделированию экономики применялись в основном модели детерминистского типа. В этих моделях все параметры предполагаются точно известными. Однако детерминистские модели неправильно понимать в механическом духе и отождествлять их с моделями, которые лишены всех «степеней выбора» (возможностей выбора) и имеют единственное допустимое решение. Классическим представителем жестко детерминистских моделей является оптимизационная модель народного хозяйства, применяемая для определения наилучшего варианта экономического развития среди множества допустимых вариантов.
В результате накопления опыта использования жестко детерминистских моделей были созданы реальные возможности успешного применения более совершенной методологии моделирования экономических процессов, учитывающих стохастику и неопределенность. Здесь можно выделить два основных направления исследований. Во-первых, усовершенствуется методика использования моделей жестко детерминистского типа: проведение многовариантных расчетов и модельных экспериментов с вариацией конструкции модели и ее исходных данных; изучение устойчивости и надежности получаемых решений, выделение зоны неопределенности; включение в модель резервов, применение приемов, повышающих приспособляемость экономических решений к вероятным и непредвидимым ситуациям. Во-вторых, получают распространение модели, непосредственно отражающие стохастику и неопределенность экономических процессов и использующие соответствующий математический аппарат: теорию вероятностей и математическую статистику, теорию игр и статистических решений, теорию массового обслуживания, стохастическое программирование, теорию случайных процессов.
5. Проверка адекватности моделей.
Сложность экономических процессов и явлений и другие отмеченные выше особенности экономических систем затрудняют не только построение математических моделей, но и проверку их адекватности, истинности получаемых результатов.
Специфика верификации нормативных моделей экономики состоит в том, что они, как правило, «конкурируют» с другими, уже нашедшими практическое применение методами планирования и управления. При этом далеко не всегда можно поставить чистый эксперимент по верификации модели, устранив влияние других управляющих воздействий на моделируемый объект.
Несмотря на отмеченные усложняющие обстоятельства, соответствие модели фактам и тенденциям реальной экономической жизни остается важнейшим критерием, определяющим направления совершенствования моделей. Всесторонний анализ выявляемых расхождений между действительностью и моделью, сопоставление результатов по модели с результатами, полученными иными методами, помогают выработать пути коррекции моделей.
Значительная роль в проверке моделей принадлежит логическому анализу, в том числе средствами самого математического моделирования. Такие формализованные приемы верификации моделей, как доказательство существования решения в модели, проверка истинности статистических гипотез о связях между параметрами и переменными модели, сопоставления размерности величин и т.д., позволяют сузить класс потенциально «правильных» моделей.
Внутренняя непротиворечивость предпосылок модели проверяется также путем сравнения друг с другом получаемых с ее помощью следствий, а также со следствиями «конкурирующих» моделей.
Оценивая современное состояние проблемы адекватности математических моделей экономике, следует признать, что создание конструктивной комплексной методики верификации моделей, учитывающей как объективные особенности моделируемых объектов, так и особенности их познания, по-прежнему является одной из наиболее актуальных задач экономико-математических исследований.
6. Классификация экономико-математических моделей.
Математические модели экономических процессов и явлений более кратко можно назвать экономико-математическими моделями. Для классификации этих моделей используются разные основания.
Остановимся более подробно на характеристике таких классов экономико-математических моделей, с которыми связаны наибольшие особенности методологии и техники моделирования.
Выше уже показывались различия между моделями дескриптивными и нормативными. Дискриптивные модели отвечают на вопрос: как это происходит? или как это вероятнее всего может дальше развиваться?, т.е. они только объясняют наблюдаемые факты или дают вероятный прогноз. Нормативные модели отвечают на вопрос: как это должно быть?, т.е. предполагают целенаправленную деятельность. Типичным примером нормативных моделей являются модели оптимального планирования, формализующие тем или иным способом цели экономического развития, возможности и средства их достижения.
Применение дескриптивного подхода в моделировании экономики объясняется необходимостью эмпирического выявления различных зависимостей в экономике, установления статистических закономерностей экономического поведения социальных групп, изучения вероятных путей развития каких-либо процессов при неизменяющихся условиях или протекающих без внешних воздействий. Примерами дескриптивных моделей являются производственные функции и функции покупательского спроса, построенные на основе обработки статистических данных.
Является ли экономико-математическая модель дескриптивной или нормативной, зависит не только от ее математической структуры, но от характера использования этой модели. Например, модель межотраслевого баланса дескриптивна, если она используется для анализа пропорций прошлого периода. Но эта же математическая модель становится нормативной, когда она применяется для расчетов сбалансированных вариантов развития народного хозяйства, удовлетворяющих конечные потребности общества при плановых нормативах производственных затрат.
Многие экономико-математические модели сочетают признаки дескриптивных и нормативных моделей. Типична ситуация, когда нормативная модель сложной структуры объединяет отдельные блоки, которые являются частными дескриптивными моделями. Например, межотраслевая модель может включать функции покупательского спроса, описывающие поведение потребителей при изменении доходов. Подобные примеры характеризуют тенденцию эффективного сочетания дескриптивного и нормативного подходов к моделированию экономических процессов. Дескриптивный подход широко применяется в имитационном моделировании.
По характеру отражения причинно-следственных связей различают модели жестко детерминистские и модели, учитывающие случайность и неопределенность. Необходимо различать неопределенность, описываемую вероятностными законами, и неопределенность, для описания которой законы теории вероятностей неприменимы. Второй тип неопределенности гораздо более сложен для моделирования.
По способам отражения фактора времени экономико-математические модели делятся на статические и динамические. В статических моделях все зависимости относятся к одному моменту или периоду времени. Динамические модели характеризуют изменения экономических процессов во времени. По длительности рассматриваемого периода времени различаются модели краткосрочного (до года), среднесрочного (до 5 лет), долгосрочного (10-15 и более лет) прогнозирования и планирования. Само время в экономико-математических моделях может изменяться либо непрерывно, либо дискретно.
Модели экономических процессов чрезвычайно разнообразны по форме математических зависимостей. Особенно важно выделить класс линейных моделей, наиболее удобных для анализа и вычислений и получивших вследствие этого большое распространение. Различия между линейными и нелинейными моделями существенны не только с математической точки зрения, но и в теоретико-экономическом отношении, поскольку многие зависимости в экономике носят принципиально нелинейный характер: эффективность использования ресурсов при увеличении производства, изменение спроса и потребления населения при увеличении производства, изменение спроса и потребления населения при росте доходов и т.п. Теория «линейной экономики» существенно отличается от теории «нелинейной экономики». От того, предполагаются ли множества производственных возможностей подсистем (отраслей, предприятий) выпуклыми или же невыпуклыми, существенно зависят выводы о возможности сочетания централизованного планирования и хозяйственной самостоятельности экономических подсистем.
Для моделей народнохозяйственного уровня важно деление на агрегированные и детализированные.
В зависимости от того, включают ли народнохозяйственные модели пространственные факторы и условия или не включают, различают модели пространственные и точечные.
Таким образом, общая классификация экономико-математических моделей включает более десяти основных признаков. С развитием экономико-математических исследований проблема классификации применяемых моделей усложняется. Наряду с появлением новых типов моделей (особенно смешанных типов) и новых признаков их классификации осуществляется процесс интеграции моделей разных типов в более сложные модельные конструкции.
7. Этапы экономико-математического моделирования.
Основные этапы процесса моделирования уже рассматривались выше. В различных отраслях знаний, в том числе и в экономике, они приобретают свои специфические черты. Проанализируем последовательность и содержание этапов одного цикла экономико-математического моделирования.
Знание общих свойств модели имеет столь важное значение, часто ради доказательства подобных свойств исследователи сознательно идут на идеализацию первоначальной модели. И все же модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию. В тех случаях, когда аналитическими методами не удается выяснить общих свойств модели, а упрощения модели приводят к недопустимым результатам, переходят к численным методам исследования.
4. Подготовка исходной информации. Моделирование предъявляет жесткие требования к системе информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования. При этом принимается во внимание не только принципиальная возможность подготовки информации (за определенные сроки), но и затраты на подготовку соответствующих информационных массивов. Эти затраты не должны превышать эффект от использования дополнительной информации.
В процессе подготовки информации широко используются методы теории вероятностей, теоретической и математической статистики. При системном экономико-математическом моделировании исходная информация, используемая в одних моделях, является результатом функционирования других моделей.
5. Численное решение. Этот этап включает разработку алгоритмов для численного решения задачи, составления программ на ЭВМ и непосредственное проведение расчетов. Трудности этого этапа обусловлены прежде всего большой размерностью экономических задач, необходимостью обработки значительных массивов информации.
Обычно расчеты по экономико-математической модели носят многовариантный характер. Благодаря высокому быстродействию современных ЭВМ удается проводить многочисленные «модельные» эксперименты, изучая «поведение» модели при различных изменениях некоторых условий. Исследование, проводимое численными методами, может существенно дополнить результаты аналитического исследования, а для многих моделей оно является единственно осуществимым. Класс экономических задач, которые можно решать численными методами, значительно шире, чем класс задач, доступных аналитическому исследованию.
6. Анализ численных результатов и их применение. На этом заключительном этапе цикла встает вопрос о правильности и полноте результатов моделирования, о степени практической применимости последних.
Математические методы проверки могут выявлять некорректные построения модели и тем самым сужать класс потенциально правильных моделей. Неформальный анализ теоретических выводов и численных результатов, получаемых посредством модели, сопоставление их с имеющимися знаниями и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели, ее информационного и математического обеспечения.
Взаимосвязи этапов. На рис. 1 изображены связи между этапами одного цикла экономико-математического моделирования.
Обратим внимание на возвратные связи этапов, возникающие вследствие того, что в процессе исследования обнаруживаются недостатки предшествующих этапов моделирования.
Уже на этапе построения модели может выясниться, что постановка задачи противоречива или приводит к слишком сложной математической модели. В соответствии с этим исходная постановка задачи корректируется. Далее математический анализ модели (этап 3) может показать, что небольшая модификация постановки задачи или ее формализации дает интересный аналитический результат.
Поскольку экономико-математические задачи могут быть сложны по своей структуре, иметь большую размерность, то часто случается, что известные алгоритмы и программы для ЭВМ не позволяют решить задачу в первоначальном виде. Если невозможно в короткий срок разработать новые алгоритмы и программы, исходную постановку задачи и модель упрощают: снимают и объединяют условия, уменьшают число факторов, нелинейные соотношения заменяют линейными, усиливают детерминизм модели и т.д.
Недостатки, которые не удается исправить на промежуточных этапах моделирования, устраняются в последующих циклах. Но результаты каждого цикла имеют и вполне самостоятельное значение. Начав исследование с построения простой модели, можно быстро получить полезные результаты, а затем перейти к созданию более совершенной модели, дополняемой новыми условиями, включающей уточненные математические зависимости.
По мере развития и усложнения экономико-математического моделирования его отдельные этапы обособляются в специализированные области исследований, усиливаются различия между теоретико-аналитическими и прикладными моделями, происходит дифференциация моделей по уровням абстракции и идеализации.
8. Роль прикладных экономико-математических исследований.
Можно выделить, по крайней мере, четыре аспекта применения математических методов в решении практических проблем.
1. Совершенствование системы экономической информации. Математические методы позволяют упорядочить систему экономической информации, выявлять недостатки в имеющейся информации и вырабатывать требования для подготовки новой информации или ее корректировки. Разработка и применение экономико-математических моделей указывают пути совершенствования экономической информации, ориентированной на решение определенной системы задач планирования и управления. Прогресс в информационном обеспечении планирования и управления опирается на бурно развивающиеся технические и программные средства информатики.
2. Интенсификация и повышение точности экономических расчетов. Формализация экономических задач и применение ЭВМ многократно ускоряют типовые, массовые расчеты, повышают точность и сокращают трудоемкость, позволяют проводить многовариантные экономические обоснования сложных мероприятий, недоступные при господстве «ручной» технологии.
3. Углубление количественного анализа экономических проблем. Благодаря применению метода моделирования значительно усиливаются возможности конкретного количественного анализа; изучение многих факторов, оказывающих влияние на экономические процессы, количественная оценка последствий изменения условий развития экономических объектов и т.п.
4. Решение принципиально новых экономических задач. Посредством математического моделирования удается решать такие экономические задачи, которые иными средствами решить практически невозможно, например: нахождение оптимального варианта народнохозяйственного плана, имитация народнохозяйственных мероприятий, автоматизация контроля за функционированием сложных экономических объектов.
Сфера практического применения метода моделирования ограничивается возможностями и эффективностью формализации экономических проблем и ситуаций, а также состоянием информационного, математического, технического обеспечения используемых моделей. Стремление во что бы то ни стало применить математическую модель может не дать хороших результатов из-за отсутствия хотя бы некоторых необходимых условий.
В соответствии с современными научными представлениями системы разработки и принятия хозяйственных решений должны сочетать формальные и неформальные методы, взаимоусиливающие и взаимодополняющие друг друга. Формальные методы являются прежде всего средством научно обоснованной подготовки материала для действий человека в процессах управления. Это позволяет продуктивно использовать опыт и интуицию человека, его способности решать плохо формализуемые задачи.
Ошибка в тексте? Выдели её мышкой и нажми