что такое модель точности
Математические модели точности



Точность является одним из основных свойств качества. Количественно она оценивается ошибкой (погрешностью) или величиной отклонения параметров от их номинальных значений. Возможные отклонения параметров определяются допуском, т. е. заранее установленным опытом или расчетом, границами изменения параметров изделия, при которых оно способно выполнять свои функции в соответствии с назначением.
Вопросы допусков наиболее полно разработаны в приборостроении для механизмов и механических устройств. Основоположником теории точности в этой области является акаденик Н. Г. Бруевич. Менее всего теория точности разработана для электронной аппаратуры. Это объясняется тем, что электронная аппаратура появилась сравнительно недавно, а ее элементная база, которая в значительной мерс определяет точность, изменяется очень быстро.
Теория точности решает следующие задачи: изучает причины возникновения ошибок, разрабатывает методы анализа и контроля точности; разрабатывает методы повышения точности.
Решение основных задач точности осуществляется через анализ точности параметров элементной базы и выходных характеристик узлов или устройств, имеющих самостоятельное целевое назначение.
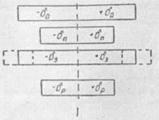
Кратко остановимся на характеристике допусков, одновременно классифицируя их по месту назначения. Различают арбитражные, производственные, эксплуатационные и ремонтные допуски (рис. 1.12).
Арбитражный допуск δа — это допуск, установленный техническими условиями или стандартами для параметра изготавливаемой или разрабатываемой аппаратуры. Такой допуск иногда называют эскизным. Устанавливается он заказчиком, разработчиком или заводом-изготовителем. Указывается значение арбитражного допуска в эскизном проекте, технических условиях (ТУ) или в техническом проекте. Этот допуск корректируется в процессе изготовления и испытаний. Часто его устанавливают экспериментальным путем.
Рис. 1.12. График,поясняющий соотношения межд допусками
Производственный допуск δп определяется производственно-технологической документацией для параметра изготовляемой аппаратуры или элемента. Он корректируется в соответствии с опытом производства. Допуск устанавливается заводом-изготовителем или разработчиком, он имеет «запас надежности» на неучтенные факторы. Производственный допуск обеспечивается арбитражным допуском в зависимости от допусков элементной базы.
Эксплуатационный допуск δЭ устанавливается инструкцией по эксплуатации для параметра эксплуатируемой аппаратуры. Назначается он только для параметров, проверяемых при эксплуатации, и должен обеспечить показатель назначения. Устанавливается эксплуатационный допуск разработчиком, заводом-изготовителем или эксплуатирующей изделие организацией.
Иногда эксплуатационный допуск подразделяют на эксплуатационно-контрольный δэк и эксплуатационно-профилактический δэп—
Ремонтный допуск δp — это допуск, устанавливаемый техническими условиями на ремонт для параметра ремонтируемой аппаратуры. Устанавливается он заводом-изготовителем или эксплуатирующем организацией.
Все перечисленные допуски предназначены для обеспечения основных функциональных показателей качества, т. е. показателей назначения, устанавливаемых тактико-техническими требованиями. Для вычислительной аппаратуры это будет, например, точность вычислений, быстродействие и т. д. Часто основные функциональные показатели и показатели назначения употребляются как равнозначные, имеющие один и тот же смысл.
Ранее отмечалось, что допуски устанавливаются для параметров. Параметры, в свою очередь, делятся на выходные и первичные. Выходные параметры характеризуют целевое назначение изделия и количественно определяют показатели назначения.
Первичные параметры — это параметры, определяемые элементами конструкции и в своей совокупности в конечном итоге формирующие выходной параметр и его допуск.
Кроме приведенной ранее классификации допусков можно привести еще одну классификацию по расположению границ допусков. По этой классификации различают:
двусторонний допуск — это допуск, обе границы которого «а» и «б» находятся в конечной области распределения параметра;
односторонний—если граница «а» или «в» находится в бесконечности;
симметричный — если поле допуска расположено симметрично относительно номинального значения;
несимметричный — если «а»≠«в», но номинальное значение параметра лежит внутри поля допуска, т. е. между «а» и «в>.
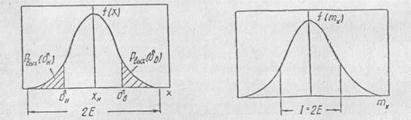
Параметры элементов и деталей, выпускаемых промышленностью, обычно определяются не законами распределения и не числовыми характеристиками, а допусками на изделие. Взаимосвязь между числовыми характеристиками, законом рассеяния параметров и допусков легко установить. Предположим, что известна плотность распределения параметра f(x) (рис 1.13). Площадь, характеризующая вероятность отбраковки изделия по выходу их параметров за нижнюю границу допусков, составляет Рвых(δн). Площадь, характеризующая вероятность отбраковки изделий по выходу их параметров за верхнюю границу допуска, составляет Рвых(δв).
В реальных условиях обычно поле допуска и поле рассеяния параметра совпадают, а сам допуск при установившемся технологическом процессе больше 3σ. Поле допуска равно 2δ, поле рассеяния параметра — 2Е, номинальное значение параметра — хн, а середина поля допуска — хс, которая в рассматриваемом случае совпадает с хн.
При оценке качества функционирования аппаратуры по допускам на параметры, теория точности и надежности сливаются. Особенно это слияние очевидно при анализе постепенных отказов.
В основе оценок точности изделий лежат измерения, поэтому необходим свод определенных правил и аппарат обработки результатов измерений. Этими вопросами занимается математическая статистика.
Введем некоторые понятия и определения, которые встретятся при изложении материала. Назовем полную систему элементов изделий или чисел, подлежащих исследованиям, генеральной совокупностью. Часть генеральной совокупности, отобранной для исследований, называют выборкой. Следовательно, выборка характеризуется объемом, который должен быть таким, чтобы выборка была представительной, а ее оценка — состоятельной, т. е. довольно полно характеризующей свойства генеральной 1 совокупности.
О представительности и состоятельности выборки судят по оценке, т. е. по той величине, которая получена после обработки результатов измерений.
Выборочная оценка считается состоятельной, а выборка представительной в том случае, если вероятность того, что разность между выборочным математическим ожиданием и теоретическим
Рис. 1.13. Функция плотности распределения параметра
Рис. 1.14. График плотности распределения математического ожидания
его значением меньше некоторой наперед выбранной величины е, стремится к единице P[(mx-mT)] Uпор)→1.
Оценка качества в задачах классификации и регрессии
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
Оценки качества классификации [ править ]
Матрица ошибок (англ. Сonfusion matrix) [ править ]
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок). Допустим, что у нас есть два класса [math]y = \< 0, 1 \>[/math] и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика ( [math]y = 1 [/math] ) можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
| [math]y = 1[/math] | [math]y = 0[/math] | |
| [math]a ( x ) = 1[/math] | Истинно-положительный (True Positive — TP) | Ложно-положительный (False Positive — FP) |
| [math]a ( x ) = 0[/math] | Ложно-отрицательный (False Negative — FN) | Истинно-отрицательный (True Negative — TN) |
Здесь [math]a ( x )[/math] — это ответ алгоритма на объекте, а [math]y [/math] — истинная метка класса на этом объекте. Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
Аккуратность (англ. Accuracy) [ править ]
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5). Тогда accuracy:
[math] accuracy = \dfrac<5+90> <5+90+10+5>= 86,4 [/math]
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
[math] accuracy = \dfrac<0+100> <0+100+0+10>= 90,9 [/math]
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Точность (англ. Precision) [ править ]
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
[math] Precision = \dfrac
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall) [ править ]
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
[math] Recall = \dfrac
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
F-мера (англ. F-score) [ править ]
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок. Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где [math]β[/math] принимает значения в диапазоне [math]0\lt β\lt 1[/math] если вы хотите отдать приоритет точности, а при [math]β\gt 1[/math] приоритет отдается полноте. При [math]β=1[/math] формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют [math]F_1[/math] ).
Интерпретируемая модель машинного обучения. Часть 1
Всем привет. До старта курса «Machine Learning» остается чуть больше недели. В преддверии начала занятий мы подготовили полезный перевод, который будет интересен как нашим студентам, так и всем читателям блога. Начнем.
Пора избавиться от черных ящиков и укрепить веру в машинное обучение!
В своей книге “Interpretable Machine Learning” Кристоф Мольнар прекрасно выделяет суть интерпретируемости Машинного Обучения с помощью следующего примера: Представьте, что вы эксперт Data Science, и в свободное время пытаетесь спрогнозировать куда ваши друзья отправятся в отпуск летом, основываясь на их данных из facebook и twitter. Итак, если прогноз окажется верным, то ваши друзья будут считать вас волшебником, который может видеть будущее. Если прогнозы будут неверны, то это не принесет вреда ничему, кроме вашей репутации аналитика. Теперь представим, что это был не просто забавный проект, а к нему были привлечены инвестиции. Скажем, вы хотели инвестировать в недвижимость, где ваши друзья, вероятно, будут отдыхать. Что произойдёт, если предсказания модели будут неудачными? Вы потеряете деньги. Пока модель не оказывает существенного влияния, ее интерпретируемость не имеет большого значения, но когда есть финансовые или социальные последствия, связанные с предсказаниями модели, ее интерпретируемость приобретает совершенно другое значение.
Объяснимое машинное обучение
Интерпретировать, значит, объяснить или показать в понятных терминах. В контексте ML-системы, интерпретируемость – это способность объяснить ее действие или показать его в понятном человеку виде.
Модели машинного обучения многие люди окрестили «черными ящиками». Это означает, что несмотря на то, что мы можем получить от них точный прогноз, мы не можем понятно объяснить или понять логику их составления. Но каким образом можно извлечь инсайты из модели? Какие вещи следует иметь в виду и какие инструменты нам понадобятся для этого? Это важные вопросы, которые приходят на ум, когда речь идет об интерпретируемости модели.
Важность интерпретируемости
Вопрос, которым задаются некоторые люди, звучит как, почему бы просто не радоваться тому, что мы получаем конкретный результат работы модели, почему так важно знать, как было принято то или иное решение? Ответ кроется в том, что модель может оказывать определенное влияние на последующие события в реальном мире. Для моделей, которые предназначены для рекомендации фильмов интерпретируемость будет гораздо менее важна, чем для тех моделей, которые используются для прогнозирования результата воздействия медицинского препарата.
«Проблема заключается в том, что всего одна метрика, такая как точность классификации, является недостаточным описанием большинства реальных задач.» (Доши-Велес и Ким 2017)
Вот большая картинка про объяснимое машинное обучение. В каком-то смысле мы захватываем мир (а точнее информацию из него), собирая необработанные данные и используя их для дальнейших прогнозов. По сути, интерпретируемость – это всего лишь еще один слой модели, который помогает людям понять весь процесс.
Некоторые из преимуществ, которые приносит интерпретируемость:
Методы Интерпретации моделей
Теория имеет смысл только до тех пор, пока мы можем применять ее на практике. В случае, если вы действительно хотите разобраться с этой темой, можете попробовать пройти курс Machine Learning Explainability от Kaggle. В нем вы найдете правильное соотношение теории и кода, чтобы понять концепции и уметь применять на практике к реальным кейсам концепции интерпретируемости (объяснимости) моделей.
Нажмите на скриншот ниже, чтобы перейти непосредственно на страницу курса. Если вы хотите сначала получить краткий обзор темы, продолжайте чтение.
Инсайты, которые можно извлечь из моделей
Для понимания модели нам потребуются следующие инсайты:
Давайте обсудим несколько методов, которые помогают извлекать вышеперечисленные инсайты из модели:
Permutation Importance
Какие признаки модель считает важными? Какие признаки оказывают наибольшее влияние? Эта концепция называется важностью признаков (feature importance), а Permutation Importance – это метод, широко используемый для вычисления важности признаков. Он помогает нам увидеть, в какой момент модель выдает неожиданные результаты, он же помогает нам показать другим, что наша модель работает именно так, как нужно.
Permutation Importance работает для многих оценок scikit-learn. Идея проста: Произвольным образом переставить или перетасовать один столбец в наборе датасета валидации, оставив все остальные столбцы нетронутыми. Признак считается «важным», если точность модели падает и его изменение вызывает увеличение ошибок. С другой стороны, признак считается «неважным», если перетасовка его значений не влияет на точность модели.
Как это работает?
Permutation Importance вычисляется с использованием библиотеки ELI5. ELI5 – это библиотека в Python, которая позволяет визуализировать и отлаживать различные модели машинного обучения с помощью унифицированного API. Она имеет встроенную поддержку для нескольких ML-фреймворков и обеспечивает способы интерпретации black-box модели.
Интерпретация
Практика
А теперь, чтобы посмотреть на полный пример и проверить правильно ли вы все поняли, перейдите на страницу Kaggle по ссылке.
Вот и подошла к концу первая часть перевода. Пишите ваши комментарии и дл встречи на курсе!
Оценка моделей ML/DL: матрица ошибок, Accuracy, Precision и Recall
В компьютерном зрении обнаружение объекта — это проблема определения местоположения одного или нескольких объектов на изображении. Помимо традиционных методов обнаружения, продвинутые модели глубокого обучения, такие как R-CNN и YOLO, могут обеспечить впечатляющие результаты при различных типах объектов. Эти модели принимают изображение в качестве входных данных и возвращают координаты прямоугольника, ограничивающего пространство вокруг каждого найденного объекта.
В этом руководстве обсуждается матрица ошибок и то, как рассчитываются precision, recall и accuracy метрики.
Здесь мы рассмотрим:
Матрица ошибок для бинарной классификации
В бинарной классификации каждая выборка относится к одному из двух классов. Обычно им присваиваются такие метки, как 1 и 0, или положительный и отрицательный (Positive и Negative). Также могут использоваться более конкретные обозначения для классов: злокачественный или доброкачественный (например, если проблема связана с классификацией рака), успех или неудача (если речь идет о классификации результатов тестов учащихся).
Такие наименования нужны в первую очередь для того, чтобы нам, людям, было проще различать классы. Для модели более важна числовая оценка. Обычно при передаче очередного набора данных на выходе вы получите не метку класса, а числовой результат. Например, когда эти семь семплов вводятся в модель, каждому классу будут назначены следующие значения:
На основании полученных оценок каждой выборке присваивается соответствующий класс. Такое преобразование числовых результатов в метки происходит с помощью порогового значения. Данное граничное условие является гиперпараметром модели и может быть определено пользователем. Например, если порог равен 0.5, тогда любая оценка, которая больше или равна 0.5, получает положительную метку. В противном случае — отрицательную. Вот предсказанные алгоритмом классы:
Сравните достоверные и полученные метки — мы имеем 4 верных и 3 неверных предсказания. Стоит добавить, что изменение граничного условия отражается на результатах. Например, установка порога, равного 0.6, оставляет только два неверных прогноза.
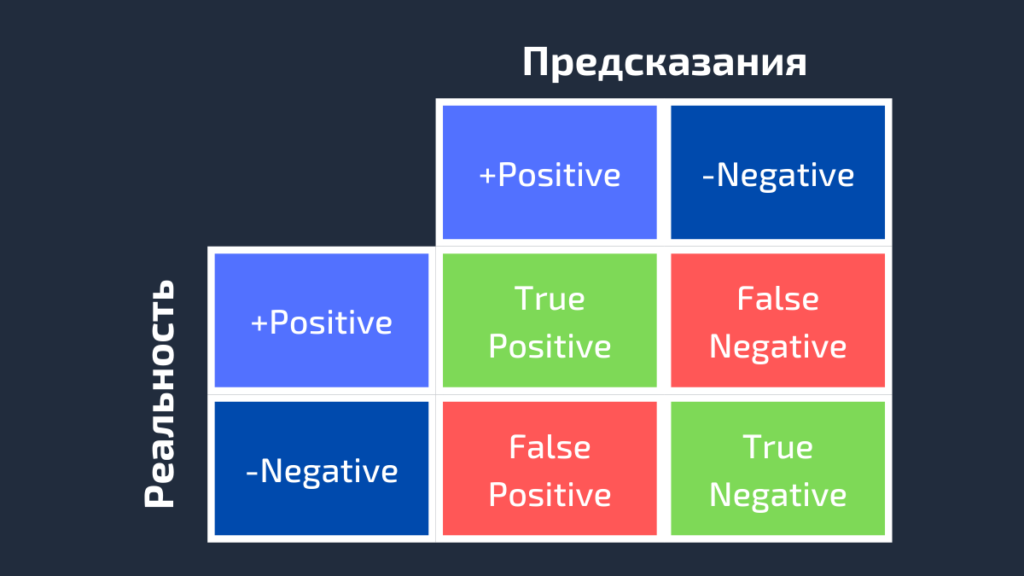
Для получения дополнительной информации о характеристиках модели используется матрица ошибок (confusion matrix). Матрица ошибок помогает нам визуализировать, «ошиблась» ли модель при различении двух классов. Как видно на следующем рисунке, это матрица 2х2. Названия строк представляют собой эталонные метки, а названия столбцов — предсказанные.
Четыре элемента матрицы (клетки красного и зеленого цвета) представляют собой четыре метрики, которые подсчитывают количество правильных и неправильных прогнозов, сделанных моделью. Каждому элементу дается метка, состоящая из двух слов:
True, если получено верное предсказание, то есть эталонные и предсказанные метки классов совпадают, и False, когда они не совпадают. Positive или Negative — названия предсказанных меток.
Таким образом, всякий раз, когда прогноз неверен, первое слово в ячейке False, когда верен — True. Наша цель состоит в том, чтобы максимизировать показатели со словом «True» (True Positive и True Negative) и минимизировать два других (False Positive и False Negative). Четыре метрики в матрице ошибок представляют собой следующее:
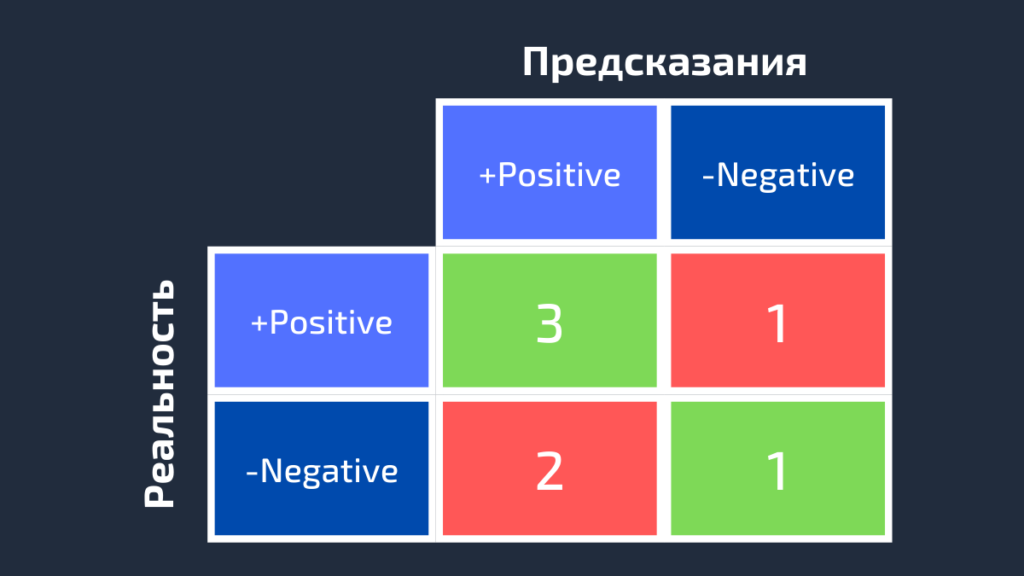
Мы можем рассчитать эти четыре показателя для семи предсказаний, использованных нами ранее. Полученная матрица ошибок представлена на следующем рисунке.
Вот так вычисляется матрица ошибок для задачи двоичной классификации. Теперь посмотрим, как решить данную проблему для большего числа классов.
Матрица ошибок для мультиклассовой классификации
Что, если у нас более двух классов? Как вычислить эти четыре метрики в матрице ошибок для задачи мультиклассовой классификации? Очень просто!
Предположим, имеется 9 семплов, каждый из которых относится к одному из трех классов: White, Black или Red. Вот достоверные метки для 9 выборок:
После загрузки данных модель делает следующее предсказание:
Для удобства сравнения здесь они расположены рядом.
Перед вычислением матрицы ошибок необходимо выбрать целевой класс. Давайте назначим на эту роль класс Red. Он будет отмечен как Positive, а все остальные отмечены как Negative.
11111111111111111111111После замены остались только два класса (Positive и Negative), что позволяет нам рассчитать матрицу ошибок, как было показано в предыдущем разделе. Стоит заметить, что полученная матрица предназначена только для класса Red.
Далее для класса White заменим каждое его вхождение на Positive, а метки всех остальных классов на Negative. Мы получим такие достоверные и предсказанные метки:
На следующей схеме показана матрица ошибок для класса White.
Точно так же может быть получена матрица ошибок для Black.
Расчет матрицы ошибок с помощью Scikit-Learn
Следующий код вычисляет матрицу ошибок для примера двоичной классификации, который мы обсуждали ранее.
Обратите внимание, что порядок метрик отличается от описанного выше. Например, показатель True Positive находится в правом нижнем углу, а True Negative — в верхнем левом углу. Чтобы исправить это, мы можем перевернуть матрицу.
В оставшейся части этого текста мы сосредоточимся только на двух классах. В следующем разделе обсуждаются три ключевых показателя, которые рассчитываются на основе матрицы ошибок.
Accuracy, Precision и Recall
Как мы уже видели, матрица ошибок предлагает четыре индивидуальных показателя. На их основе можно рассчитать другие метрики, которые предоставляют дополнительную информацию о поведении модели:
В следующих подразделах обсуждается каждый из этих трех показателей.
Метрика Accuracy
Accuracy — это показатель, который описывает общую точность предсказания модели по всем классам. Это особенно полезно, когда каждый класс одинаково важен. Он рассчитывается как отношение количества правильных прогнозов к их общему количеству.
Рассчитаем accuracy с помощью Scikit-learn на основе ранее полученной матрицы ошибок. Переменная acc содержит результат деления суммы True Positive и True Negative метрик на сумму всех значений матрицы. Таким образом, accuracy, равная 0.5714, означает, что модель с точностью 57,14% делает верный прогноз.
Стоит учесть, что метрика accuracy может быть обманчивой. Один из таких случаев — это несбалансированные данные. Предположим, у нас есть всего 600 единиц данных, из которых 550 относятся к классу Positive и только 50 — к Negative. Поскольку большинство семплов принадлежит к одному классу, accuracy для этого класса будет выше, чем для другого.
Если модель сделала 530 правильных прогнозов из 550 для класса Positive, по сравнению с 5 из 50 для Negative, то общая accuracy равна (530 + 5) / 600 = 0.8917. Это означает, что точность модели составляет 89.17%. Полагаясь на это значение, вы можете подумать, что для любой выборки (независимо от ее класса) модель сделает правильный прогноз в 89.17% случаев. Это неверно, так как для класса Negative модель работает очень плохо.
Precision
Precision представляет собой отношение числа семплов, верно классифицированных как Positive, к общему числу выборок с меткой Positive (распознанных правильно и неправильно). Precision измеряет точность модели при определении класса Positive.
Когда модель делает много неверных Positive классификаций, это увеличивает знаменатель и снижает precision. С другой стороны, precision высока, когда:
Представьте себе человека, который пользуется всеобщим доверием; когда он что-то предсказывает, окружающие ему верят. Метрика precision похожа на такого персонажа. Если она высока, вы можете доверять решению модели по определению очередной выборки как Positive. Таким образом, precision помогает узнать, насколько точна модель, когда она говорит, что семпл имеет класс Positive.
Основываясь на предыдущем обсуждении, вот определение precision:
Precision отражает, насколько надежна модель при классификации Positive-меток.
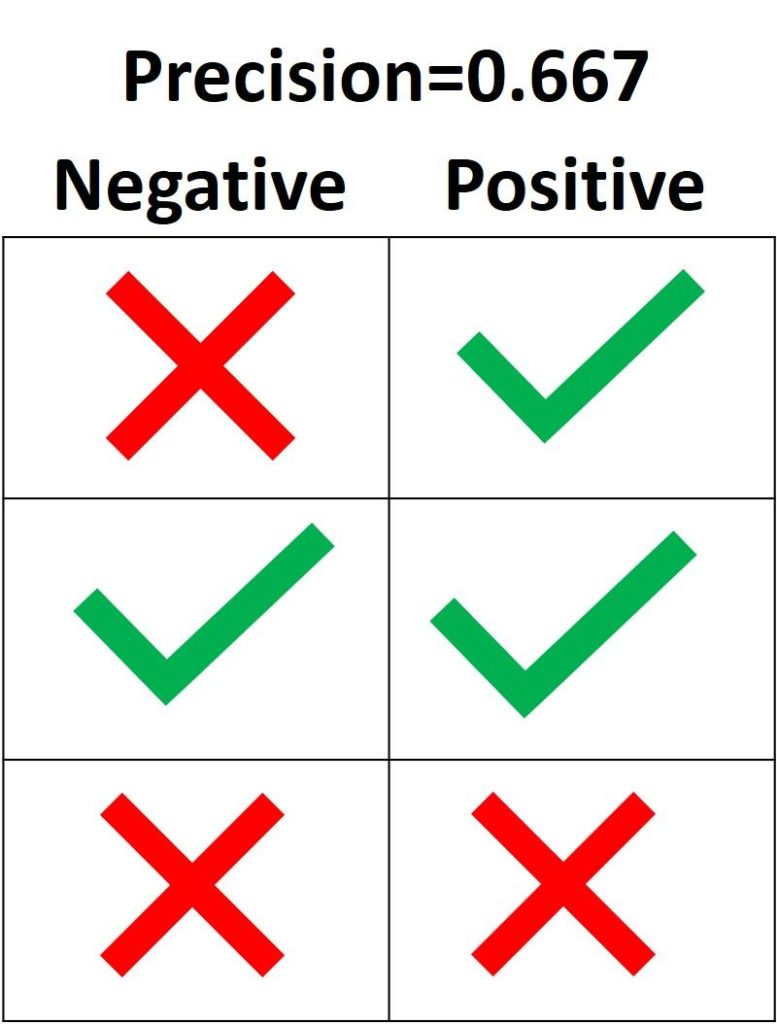
На следующем изображении зеленая метка означает, что зеленый семпл классифицирован как Positive, а красный крест – как Negative. Модель корректно распознала две Positive выборки, но неверно классифицировала один Negative семпл как Positive. Из этого следует, что метрика True Positive равна 2, когда False Positive имеет значение 1, а precision составляет 2 / (2 + 1) = 0.667. Другими словами, процент доверия к решению модели, что выборка относится к классу Positive, составляет 66.7%.
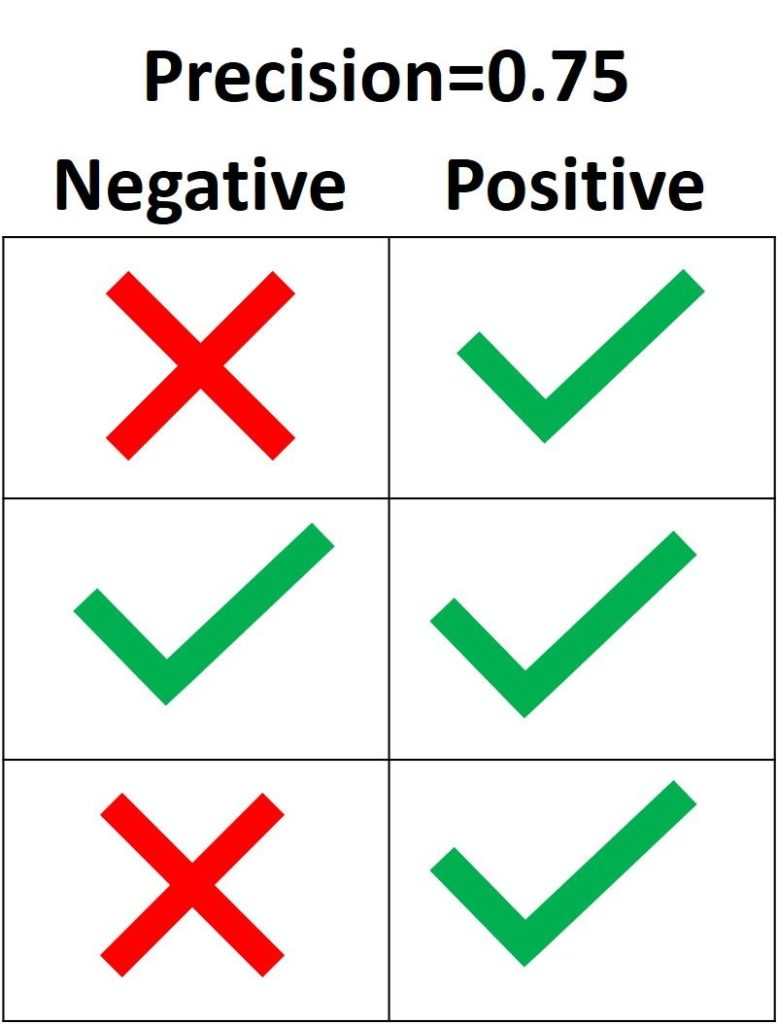
Цель precision – классифицировать все Positive семплы как Positive, не допуская ложных определений Negative как Positive. Согласно следующему рисунку, если все три Positive выборки предсказаны правильно, но один Negative семпл классифицирован неверно, precision составляет 3 / (3 + 1) = 0.75. Таким образом, утверждения модели о том, что выборка относится к классу Positive, корректны с точностью 75%.
Единственный способ получить 100% precision — это классифицировать все Positive выборки как Positive без классификации Negative как Positive.
Recall
Recall рассчитывается как отношение числа Positive выборок, корректно классифицированных как Positive, к общему количеству Positive семплов. Recall измеряет способность модели обнаруживать выборки, относящиеся к классу Positive. Чем выше recall, тем больше Positive семплов было найдено.
Recall заботится только о том, как классифицируются Positive выборки. Эта метрика не зависит от того, как предсказываются Negative семплы, в отличие от precision. Когда модель верно классифицирует все Positive выборки, recall будет 100%, даже если все представители класса Negative были ошибочно определены как Positive. Давайте посмотрим на несколько примеров.
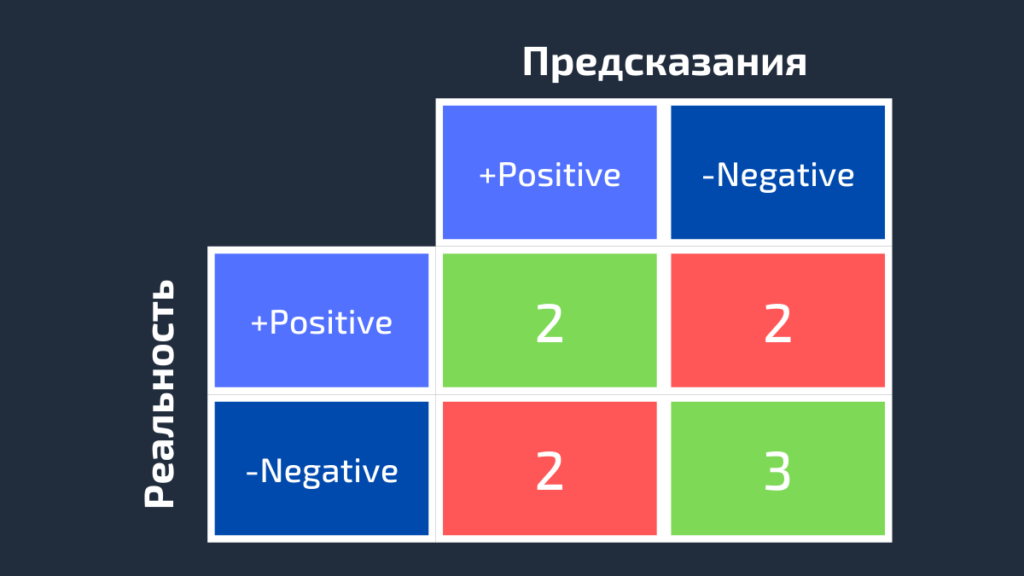
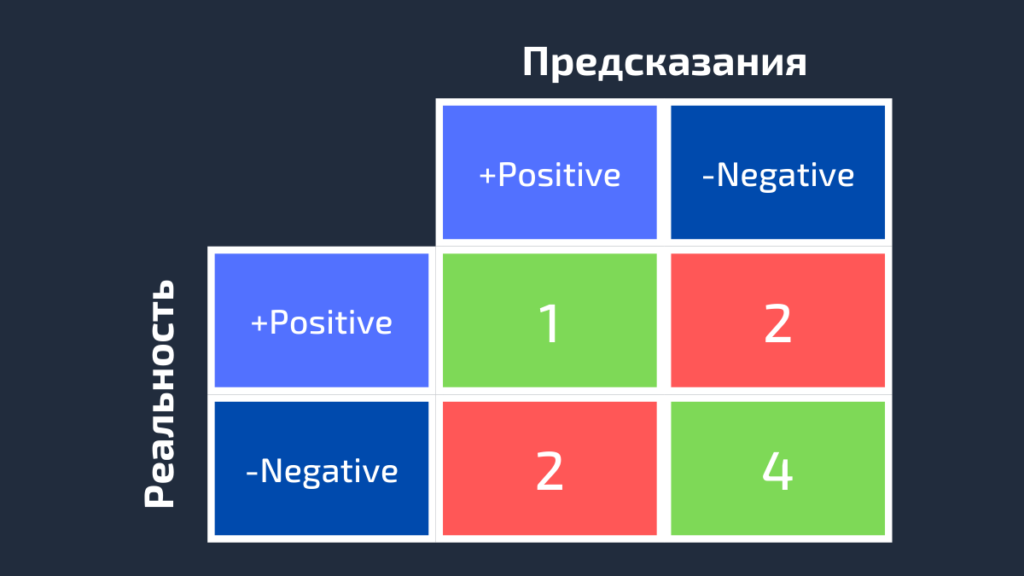
На следующем изображении представлены 4 разных случая (от A до D), и все они имеют одинаковый recall, равный 0.667. Представленные примеры отличаются только тем, как классифицируются Negative семплы. Например, в случае A все Negative выборки корректно определены, а в случае D – наоборот. Независимо от того, как модель предсказывает класс Negative, recall касается только семплов относящихся к Positive.
Из 4 случаев, показанных выше, только 2 Positive выборки определены верно. Таким образом, метрика True Positive равна 2. False Negative имеет значение 1, потому что только один Positive семпл классифицируется как Negative. В результате recall будет равен 2 / (2 + 1) = 2/3 = 0.667.
Поскольку не имеет значения, как предсказываются объекты класса Negative, лучше их просто игнорировать, как показано на следующей схеме. При расчете recall необходимо учитывать только Positive выборки.
Что означает, когда recall высокий или низкий? Если recall имеет большое значение, все Positive семплы классифицируются верно. Следовательно, модели можно доверять в ее способности обнаруживать представителей класса Positive.
На следующем изображении recall равен 1.0, потому что все Positive семплы были правильно классифицированы. Показатель True Positive равен 3, а False Negative – 0. Таким образом, recall вычисляется как 3 / (3 + 0) = 1. Это означает, что модель обнаружила все Positive выборки. Поскольку recall не учитывает, как предсказываются представители класса Negative, могут присутствовать множество неверно определенных Negative семплов (высокая False Positive метрика).
С другой стороны, recall равен 0.0, если не удается обнаружить ни одной Positive выборки. Это означает, что модель обнаружила 0% представителей класса Positive. Показатель True Positive равен 0, а False Negative имеет значение 3. Recall будет равен 0 / (0 + 3) = 0.
Когда recall имеет значение от 0.0 до 1.0, это число отражает процент Positive семплов, которые модель верно классифицировала. Например, если имеется 10 экземпляров Positive и recall равен 0.6, получается, что модель корректно определила 60% объектов класса Positive (т.е. 0.6 * 10 = 6).
Подобно precision_score(), функция repl_score() из модуля sklearn.metrics вычисляет recall. В следующем блоке кода показан пример ее использования.
После определения precision и recall давайте кратко подведем итоги:
Некоторые вопросы для проверки понимания:
Precision или Recall?
Решение о том, следует ли использовать precision или recall, зависит от типа вашей проблемы. Если цель состоит в том, чтобы обнаружить все positive выборки (не заботясь о том, будут ли negative семплы классифицированы как positive), используйте recall. Используйте precision, если ваша задача связана с комплексным предсказанием класса Positive, то есть учитывая Negative семплы, которые были ошибочно классифицированы как Positive.
Представьте, что вам дали изображение и попросили определить все автомобили внутри него. Какой показатель вы используете? Поскольку цель состоит в том, чтобы обнаружить все автомобили, используйте recall. Такой подход может ошибочно классифицировать некоторые объекты как целевые, но в конечном итоге сработает для предсказания всех автомобилей.
Теперь предположим, что вам дали снимок с результатами маммографии, и вас попросили определить наличие рака. Какой показатель вы используете? Поскольку он обязан быть чувствителен к неверной идентификации изображения как злокачественного, мы должны быть уверены, когда классифицируем снимок как Positive (то есть с раком). Таким образом, предпочтительным показателем в данном случае является precision.
Вывод
В этом руководстве обсуждалась матрица ошибок, вычисление ее 4 метрик (true/false positive/negative) для задач бинарной и мультиклассовой классификации. Используя модуль metrics библиотеки Scikit-learn, мы увидели, как получить матрицу ошибок в Python.