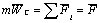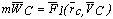что такое модель материальной точки

Что такое модель материальной точки

Реальные движения тел порой так сложны, что при их изучении необходимо постараться пренебречь несущественными для рассмотрения деталями. С этой целью в физике прибегают к моделированию, т. е. к составлению упрощённой схемы (модели) явления, позволяющей понять его основную суть, не отвлекаясь на второстепенные обстоятельства. Среди общепринятых физических моделей важную роль в механике играют модель материальной точки и модель абсолютно твёрдого тела.

Материальная точка – это тело, геометрическими размерами которого в условиях задачи можно пренебречь и считать, что вся масса тела сосредоточена в геометрической точке.

Абсолютно твёрдое тело (просто твёрдое тело) – это система, состоящая из совокупности материальных точек, расстояния между которыми в условиях задачи можно считать неизменными.

Модель материальной точки применима прежде всего в случаях, когда размеры тела много меньше других характерных размеров в условиях конкретной задачи. Например, можно пренебречь размерами искусственного спутника по сравнению с расстоянием до Земли и рассматривать спутник как материальную точку. Это – верно! Но вместе с тем не стоит ограничиваться лишь подобными случаями.

Дело в том, что сложное движение реального тела можно «разложить» на два простых вида движения: поступательное и вращательное (см. Задание №1). Если при сложном движении заменить тело материальной точкой, то мы исключим из рассмотрения вращение тела, т. к. говорить о вращении точки вокруг самой себя бессмысленно (точка не имеет геометрических размеров). Следовательно, заменив тело материальной точкой при сложном движении, мы допустим ошибку. Однако часто в случаях, когда тело движется поступательно, не вращаясь, его можно считать материальной точкой независимо от размеров, формы и пройденного им пути.

Модель абсолютно твёрдого тела можно применять, когда в условиях рассматриваемой задачи деформации реального тела пренебрежимо малы. Так, например, в задании, посвящённом вопросам статики (Задание №4), мы будем изучать условия равновесия твёрдого тела и при решении задач часто применять указанную модель. Вместе с тем, данная модель неуместна, если суть задачи состоит, например, в изучении деформаций тела в результате тех или иных воздействий в процессе его движения или в состоянии покоя.

Таким образом, мы будем изучать механическое движение не самих реальных тел, а упомянутых выше моделей. Из них основной и наиболее употребимой для нас станет модель материальной точки. В то же время там, где это необходимо, мы будем ради наглядности изображать на рисунках тела не в виде точек, а в виде объектов, геометрические размеры которых не равны нулю.

Источник

Эта абстрактная модель представляет собой идеальное тело, имеющее определённую массу, размеры которого не имеют значения и не принимаются во внимание.

Такое упрощение необходимо для более простого решения различных задач, связанных с механическим движением.

Физические основы механики

Физика — это наука о природе, изучающая наиболее простые и общие свойства, присущие материальному миру. Благодаря этому, она является универсальной базой для естествознания и техники, а также состоит из большого количества отдельных дисциплин — классической и квантовой механики, теории относительности, а также электродинамики, оптики и прочих.

Изучение физики начинается с механики — раздела, который рассматривает движение как изменение положения тела в пространстве с течением времени. Поэтому законы механики наиболее ясно выражают пространственно-временные отношения между объектами и событиями.

Основополагающие законы физики были в своё время установленны именно на основе наблюдения соответствующих явлений и экспериментов, из-за этого, за небольшим исключением, сфера их применения довольно ограничена. В частности, классическая механика распространяется лишь на медленное движение частиц и тел в макроскопических областях пространства. Перемещение на околосветовых скоростях подчиняется законам теории относительности, а свойствами микроскопических частиц занимается квантовая механика.

Классическая механика решает две основные задачи:

Решение первой задачи в своё время привело Исаака Ньютона к открытию общих принципов движения материальной точки — динамики. Вторая послужила установлению законов о сохранении импульса и энергии.

Модели и относительность

Физика относится к точным наукам — свои результаты она выражает не только на словах, но и с помощью математических соотношений и формул. Однако свойства физических тел и явлений настолько многогранны, что даже самая совершенная теория не в состоянии отобразить их во всей своей полноте. Поэтому вместо реальных объектов, наука предпочитает оперировать физическими моделями — идеализированными телами, которые отображают лишь существенные для рассмотрения явлений свойства и факторы.

В механике существует две основные модели:

Положение объекта в пространстве и его перемещение можно определить лишь относительно другого материального тела отсчёта и связанной с ним системой координат. Помимо этого, для описания движения необходимо пользоваться общепринятым и согласованным принципом фиксации моментов, а также иметь возможность проведения измерений временных промежутков во всех точках пространства.

Совокупность тела отсчёта, системы координат и неподвижного относительно неё хронометра называют системой отсчёта.

Таким образом, местоположение и перемещение любого объекта во вселенной может быть определено лишь относительно конкретной точки, от которой ведётся отсчёт. В то же время выбор системы отсчёта является произвольным и определяется лишь удобством для описания движения в заданных условиях. Отсюда следует, что положение объекта и его перемещение в пространстве является относительным по определению.

Понятие материальной точки

В отличие от геометрической точки, не имеющей никаких материальных свойств и обладающей лишь одной пространственной координатой, материальная может иметь массу, электрический заряд и прочие характеристики, необходимые для решения конкретной задачи.

Определение материальной точки в физике необходимо ввести для упрощения расчётов. Очевидно, что для описания движения такой абстрактной модели требуется минимальное количество вычислительных ресурсов.

Как правило, точке приписывается масса реального объекта, а остальные характеристики опускаются. Это можно делать лишь в том случае, когда перемещение, совершаемое наблюдаемым телом, несоизмеримо больше его размера. К примеру, для описания движения Земли по солнечной орбите совсем необязательно учитывать её вращение вокруг собственной оси.

Если возникла необходимость рассчитать среднюю скорость авиалайнера, следующего по определённому пути, форма его корпуса не имеет никакого значения. В таком случае самолёт являет собой пример материальной точки, которая должна пройти определённое расстояние за промежуток времени. Однако при нахождении показателя сопротивления воздуха летательный аппарат необходимо рассматривать как сложную систему.

При поступательном движении все элементы тела движутся в одном направлении, его можно принимать за точку

Несмотря на универсальность и удобство точечной модели, её применение имеет существенные ограничения. Это хорошо видно на примере разреженного газа при высокой температуре. Каждая молекула имеет очень маленький размер, несоизмеримый с путём, который она проходит в пространстве. Однако в этом случае молекулу далеко не всегда можно принять за точку. Дело в том, что колебание и вращение частиц перегретого газа создают своеобразный энергетический резервуар, и пренебрегать этими характеристиками в большинстве случаев нельзя.

Описание движения в кинематике

Кинематика — это начальный раздел механики, в котором устанавливаются понятия и величины, определяющие движение, общие соотношения между его характеристиками и способы описания. В разделе не рассматриваются условия и причины, определяющие характер движения тел. Поскольку любой предмет можно считать как систему идеальных моделей, прежде всего рассматривается кинематика одной точки.

Существует три способа описания движения и положения точки в выбранной системе отсчёта:

В классической механике для удобства используются инерциальные системы отсчёта. Их особенность заключается в том, что движение всех тел происходит равномерно и прямолинейно или же полностью отсутствует. Пространство и время в такой системе обладают изотропным и равномерным строением.

Динамика и законы Ньютона

Динамика — это раздел механики, в котором законы движения тел устанавливаются через причины, обусловливающие его характер. Основу раздела составляют 3 закона Ньютона, являющиеся обобщением результатов наблюдений и специально поставленных экспериментов. Их не получится вывести из каких-либо более простых принципов.

Законы динамики имеют важное практическое значение. На них основаны расчёты, по которым сооружаются всевозможных машины и механизмы, инженерные конструкции, космические аппараты и прочая техника.

Однако стоит заметить, что утверждения Ньютона не являются универсальными даже в рамках классической механики и выполняются лишь в инерциальных системах отсчёта.

Три закона Ньютона:

Законы Ньютона нельзя изолировать друг от друга, так как они — система органичных и взаимосвязанных утверждений. Они применяются для решения любой задачи динамики, но второй закон принято считать основным, поскольку он непосредственно оперирует основными характеристиками движения.

Для определения законов движения точки необходимо иметь достоверную и полную информацию о силах, действующих на неё.

В макроскопическом мире можно наблюдать большое количество всевозможных сил, которые являются проявлениями двух самых фундаментальных взаимодействий во вселенной — электромагнитного и гравитационного. Притяжение обусловлено гравитацией, а все остальные известные науке силы имеют электромагнитную природу.

Кратко ознакомившись с особенностями классической механики, можно понять, с какой целью используется понятие материальной точки. Нужно понимать, что физика не работают с реальными объектами, а лишь с абстрактными моделями. Это помогает облегчить теоретические построения и расчёты.

Источник

Материальная точка

Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.

Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи. [1]

При прямолинейном движении тела достаточно одной координатной оси для определения его положения.

Содержание

Особенности

Следствия

Ограничения

Ограниченность применения понятия о материальной точке видна из такого примера: в разреженном газе при высокой температуре размер каждой молекулы очень мал по сравнению с типичным расстоянием между молекулами. Казалось бы, им можно пренебречь и считать молекулу материальной точкой. Однако это не всегда так: колебания и вращения молекулы — важный резервуар «внутренней энергии» молекулы, «ёмкость» которого определяется размерами молекулы, её структурой и химическими свойствами. В хорошем приближении как материальную точку можно иногда рассматривать одноатомную молекулу (инертные газы, пары металлов, и др.), но даже у таких молекул при достаточно высокой температуре наблюдается возбуждение электронных оболочек за счёт соударений молекул, с последующим высвечиванием.

Примечания

Полезное

Смотреть что такое «Материальная точка» в других словарях:

МАТЕРИАЛЬНАЯ ТОЧКА — точка, имеющая массу. В механике понятием материальная точка пользуются в случаях, когда размеры и форма тела при изучении его движения не играют роли, а важна только масса. Практически любое тело можно рассматривать как материальную точку, если… … Большой Энциклопедический словарь

МАТЕРИАЛЬНАЯ ТОЧКА — понятие, вводимое в механике для обозначения объекта, к рый рассматривается как точка, имеющая массу. Положение М. т. в пр ве определяется как положение геом. точки, что существенно упрощает решение задач механики. Практически тело можно считать… … Физическая энциклопедия

материальная точка — Точка, обладающая массой. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика EN particle DE materialle Punkt FR point matériel … Справочник технического переводчика

МАТЕРИАЛЬНАЯ ТОЧКА — МАТЕРИАЛЬНАЯ ТОЧКА, понятие, вводимое в механике для обозначения тела, размерами и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Тело можно считать материальной… … Современная энциклопедия

МАТЕРИАЛЬНАЯ ТОЧКА — В механике: бесконечно малое тело. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910 … Словарь иностранных слов русского языка

Материальная точка — МАТЕРИАЛЬНАЯ ТОЧКА, понятие, вводимое в механике для обозначения тела, размерами и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Тело можно считать материальной… … Иллюстрированный энциклопедический словарь

материальная точка — понятие, вводимое в механике для объекта бесконечно малых размеров, имеющего массу. Положение материальной точки в пространстве определяется как положение геометрической точки, что упрощает решение задач механики. Практически любое тело можно… … Энциклопедический словарь

Материальная точка — геометрическая точка, обладающая массой; материальная точка абстрактный образ материального тела, обладающего массой и не имеющего размеров … Начала современного естествознания

материальная точка — materialusis taškas statusas T sritis fizika atitikmenys: angl. mass point; material point vok. Massenpunkt, m; materieller Punkt, m rus. материальная точка, f; точечная масса, f pranc. point masse, m; point matériel, m … Fizikos terminų žodynas

материальная точка — Точка, имеющая массу … Политехнический терминологический толковый словарь

Источник

Учебники

Журнал «Квант»

Общие

§1. Описание положения тела в пространстве

1.4 Материальная точка

Общим у геометрической и материальной точек является отсутствие собственных размеров. Материальную точку, по мере необходимости, можно «наделять» свойствами, которыми обладают реальные тела, например, массой, энергией, электрическим зарядом и так далее.

Одним из критериев применимости модели материальной точки является малость размеров тела по сравнению с расстоянием, на которое оно перемещается. Однако это условие не является абсолютно однозначным. Так, описывая движение Земли вокруг Солнца при расчете ее положения на орбите, размерами Земли можно пренебречь, считать ее материальной точкой. Однако, если нам необходимо рассчитать времена восхода и заката Солнца, модель материальной точки принципиально неприменима, так как это описание требует учета вращения Земли, учета ее размеров и формы.

Рассмотрим еще один пример. Спринтеры соревнуются на стометровой дистанции. Цель описания движения – выявить, кто из спортсменов пробегает дистанцию за меньшее время (задача чисто кинематическая). Можно ли в данной задаче считать бегуна материальной точкой? Его размеры значительно меньше дистанции забега, но достаточно ли они малы, чтобы ими можно было пренебречь? Ответ на эти вопросы зависит от требуемой точности описания. Так, на серьезных соревнованиях время измеряется с точностью 0.01 секунды, за это время бегун смещается на расстояние порядка 10 сантиметров (простая оценка, полученная исходя из средней скорости спринтера 10 м/с). Следовательно, погрешность, с которой определяется положением бегуна (10 см) меньше, чем его поперечные размеры, поэтому модель материальной точки в данном случае неприменима. Не случайно мастера спринтерского бега на финише «бросают грудь вперед», выигрывая драгоценные сотые доли секунды. Таким образом, вторым критерием применимости модели является требуемая точность описания физического явления.

В некоторых ситуациях можно использовать модель материальной точки, даже если размеры тела сравнимы и даже больше расстояний, на которое смещается тело. Это допустимо тогда, когда положение одной точки тела однозначно определяет положение всего тела. Так при скольжении бруска по наклонной плоскости, зная положение его центра (как, впрочем, и любой другой точки) можно найти положение всего тела. Если модель материальной точки оказывается неприменимой, то необходимо использовать другие более сложные модели.

Источник

МАТЕРИАЛЬНАЯ ТОЧКА

МАТЕРИАЛЬНАЯ ТОЧКА – модельное понятие (абстракция) классической механики, обозначающее тело исчезающе малых размеров, но обладающее некоторой массой.

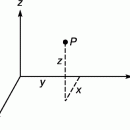
С одной стороны, материальная точка – простейший объект механики, так как его положение в пространстве определяется всего тремя числами. Например, тремя декартовыми координатами той точки пространства, в которой находится наша материальная точка.

С другой стороны, материальная точка – основной опорный объект механики, так как именно для нее сформулированы основные законы механики. Все другие объекты механики – материальные тела и среды – могут быть представлены в виде той или иной совокупности материальных точек. Например, любое тело можно «разрезать» на малые части и каждую из них принять в качестве материальной точки с соответствующей массой.

Когда можно «заменить» реальное тело материальной точкой при постановке задачи о движении тела, зависит от тех вопросов, на которые должно ответить решение формулируемой задачи.

Возможны различные подходы к вопросу об использовании модели материальной точки.

Один из них носит эмпирический характер. Считают, что модель материальной точки применима тогда, когда размеры движущихся тел пренебрежимо малы по сравнению с величиной относительных перемещений этих тел. В качестве иллюстрации можно привести Солнечную систему. Если считать, что Солнце – неподвижная материальная точка и считать оно действует на другую материальную точку-планету по закону всемирного тяготения, то задача о движении точки-планеты имеет известное решение. Среди возможных траекторий движения точки есть и такие, на которых выполняются законы Кеплера, эмпирически установленные для планет солнечной системы.

Таким образом, при описании орбитальных движений планет модель материальной точки вполне удовлетворительна. (Однако, построение математической модели таких явлений как солнечные и лунные затмения требует учета реальных размеров Солнца, Земли и Луны, хотя эти явления, очевидно, связаны с орбитальными движениями.)

Отношение диаметра Солнца к диаметру орбиты ближайшей планеты – Меркурию – составляет величину

Например, маленькая пуля размером l = 1 ÷ 2 см пролетает расстояние L = 1 ÷ 2 км, т.е. отношение 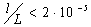, однако траектория полета (да и дальность) существенно зависит не только от массы пули, но и от ее формы, и от того, вращается ли она. Поэтому даже маленькую пулю, строго говоря, нельзя считать материальной точкой. Если в задачах внешней баллистики метаемое тело часто считают материальной точкой, то это сопровождается оговорками ряда дополнительных условий, как правило, эмпирически учитывающих реальные характеристики тела.

Если обратиться к космонавтике, то когда космический аппарат (КА) выведен на рабочую орбиту, при дальнейших расчетах траектории его полета он считается материальной точкой, так как никакие изменения формы КА не оказывают сколько-нибудь заметного влияния на траекторию. Лишь иногда, при коррекциях траектории возникает необходимость обеспечения точной ориентации реактивных двигателей в пространстве.

Когда же спускаемый отсек приблизится к поверхности Земли на расстояние

100 км, он сразу «превращается» в тело, поскольку от того, каким «боком» он входит в плотные слои атмосферы, зависит, доставит ли отсек в нужную точку Земли космонавтов и возвращаемые материалы.

Модель материальной точки оказалась практически неприемлемой для описания движений таких физических объектов микромира, как элементарные частицы, атомные ядра, электрон и т.п.

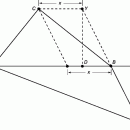
Другой подход к вопросу об использовании модели материальной точки носит рациональный характер. По закону изменения количества движения системы, примененному к отдельному телу, центр масс С тела имеет такое же ускорение, как и некоторая (назовем ее эквивалентной) материальная точка, на которую действуют те же силы, что и на тело, т.е.

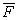
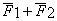
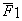
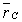
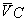
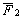
Вообще говоря, результирующая сила может быть представлена в виде суммы , где зависит только от и (радиус-вектор и скорость точки С), а – и от угловой скорости тела и его ориентации.

Если F₂ = 0, то приведенное выше соотношение превращается в уравнение движения эквивалентной материальной точки.

В этом случае говорят, что движение центра масс тела не зависит от вращательного движения тела. Таким образом, возможность использования модели материальной точки получает математическое строгое (а не только эмпирическое) обоснование.

Естественно, что на практике условие F₂ = 0 выполняется редко и обычно F₂ № 0, однако может оказаться, что F₂ в каком-то смысле мало по сравнению с F₁. Тогда можно говорить, что модель эквивалентной материальной точки является некоторым приближением при описании движения тела. Оценка точности такого приближения может быть получена математически и если эта оценка окажется приемлемой для «потребителя», то замена тела на эквивалентную материальную точку допустима, в противном случае такая замена приведет к значительным ошибкам.

Это может иметь место и тогда, когда тело движется поступательно и с точки зрения кинематики его можно «заменить» на некоторую эквивалентную точку.

Естественно, что модель материальной точки не пригодна для ответа на такие вопросы, как «почему Луна обращена к Земле лишь одной своей стороной?» Подобные явления связаны с вращательным движением тела.

Суслов Г.К. Теоретическая механика. М., «Гостехиздат», 1946
Аппель П. Теоретическая механика. тт. 1, 2. М., «Физматгиз», 1960
Четаев Н.Г. Теоретическая механика. М., «Наука», 1987
Маркеев А.П. Теоретическая механика. М., «Наука», 1999
Голубев Ю.Ф. Основы теоретической механики. М., Изд-во Моск. ун-та., 2000
Журавлев В.Ф. Основы теоретической механики. М., «Наука», 2001

Источник