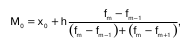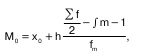что такое мода формула
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
где х о – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1 – частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе – порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число | ||||
| До 5000 | 600 | 600 | 6 | ||
| 5000-6000 | 700 | 1300 (600+700) | 13 | ||
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 ) (хо) | 2500 (fМе) | 5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 | ||
| 9000-10000 | 1500 | 9200 | 92 | ||
| Свыше 10000 | 800 | 10000 | 100 | ||
| Итого | 10000 | – | – |
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если М о о следует сделать вывод о левосторонней асимметрии ряда.
Определение моды и медианы
По данным таблицы рассчитаем моду и медиану
Диапазон по продолжительности жизни
Число стран (частота), f
Накопленная частота, f
Определение моды
Интервал, имеющий наибольшую частоту, будет являться модальным, а конкретное (дискретное) значение моды будет находиться внутри него. Рассчитать конкретное, значение моды в интервальном ряду можно по следующей формуле:
где: ХМо — нижняя граница модального интервала,
i — длина модального интервала,
fMo — частота модального интервала,
fMo-1 — частота, соответствующая предшествующему интервалу,
fMo+1 — частота, соответствующая последующему интервалу.
Самая большая частота, 37 стран, соответствует варианту 71,70 — 74,43. Этот интервал является модальным.
Определение медианы
Медиана применяется для количественной характеристики структуры и равна такому варианту, который делит ранжированную совокупность на две равные части. У одной половины совокупности признаки не больше медианы (меньше или равны), у второй — не меньше медианы (больше или равны).
Если рассматриваемый ряд интервальный, то накопленные частоты покажут нам медианный интервал. Конкретное значение медианы рассчитывается по формуле:
i — длина медианного интервала,
сумма f — сумма частот ряда (объем совокупности),
f’Me-1 — накопленная частота в интервале, предшествующем медианному,
fMe — частота медианного интервала.
Для нахождения медианного интервала нужно знать половину частот, то есть 150 : 2 = 75. В столбце «накопленные частоты» выбираем 5 интервал, так как в 4 интервале частот накопилось еще 49 стран — меньше половины. С помощью формулы найдем конкретное значение медианы, оно принадлежит медианному интервалу 71,70 — 74,43.
Разница между 74,14 и 73,61 говорит об умеренном асимметричном распределении
Наиболее часто встраивающаяся варианта
В статистике модой называется величина признака (варианта), которая чаще всего встречается в данной совокупности.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.
Распределительные средние – мода и медиана, их сущность и способы исчисления.
Данные показатели относятся к группе распределительных средних и используются для формирования обобщающей характеристики величины варьирующего признака.
Мода 

Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:

Медианный интервал не обязательно совпадает с модальным.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Мода (математика)
Мода — значение во множестве наблюдений, которое встречается наиболее часто. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.
Мода, как средняя величина, употребляется чаще для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, черный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.
См.также
Смотреть что такое «Мода (математика)» в других словарях:
МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера
Портрет итальянского Ренессанса — Сандро Боттичелли. «Портрет юноши с медалью Козимо Медичи». 1470 1477. Уффици, Флоренция Портрет итальянского … Википедия
Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия
Друга Ріка — (рус. Вторая Река) украинская поп рок группа созданная в начале 1996 года в городе Житомире, Украина Друга Ріка Жанр Поп рок Годы с … Википедия
Миланский технический университет — Оригинальное название итал. Politecnico di Milano Прежние названия итал. … Википедия
Успенский, Яков Викторович — Яков Викторович Успенский Дата рождения: 29 апреля (11 мая) 1883(1883 05 11) Место рождения: Урга, Внешняя Монголия, Империя Цин Дата смерти: 27 января … Википедия
Флоренция* — (итал. Firenze, прежде Fiorenza, лат. Florentia цветущий город ) главный город провинции Ф., до 1859 г. главный город Тосканского великого герцогства, с 1865 до 1871 г. столица Итальянского королевства, под 43°46 с. ш. и 11°17 в. д. от Гринвича,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Флоренция, город — (итал. Firenze, прежде Fiorenza, лат. Florentia цветущий город ) гл. гор. провинции Ф., до 1859 г. гл. гор. Тосканского великого герцогства, с 1865 до 1871 г. столица Итальянского королевства, под 43° 46 с. ш. и 11° 17 в. д. от Грин., на высоте,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Сейлор Мун — Главная героиня аниме «Сейлор Мун», Усаги Цукино Sailor Moon (англ.) яп. 美少女戦士セーラームーン … Википедия
Египет — I (греч. Αϊγυπτος; лат. Aegyptus; фр. Egypte; англ. Egypt; нем. Aegypten; итал. Egytto; арабск. Masz). Положение, границы. Страна Е. (в узком, историческом смысле слова) лежит между 24°5 и 31°35 северной широты и 28°50 и 34°41 восточной долготы… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Мода и медиана
Мода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда. Она показывает размер признака, свойственный значительной части совокупности, и определяется по формуле:
где х 0 нижняя граница интервала;
h – величина интервала;
f m частота интервала;
f m-1 частота предшествующего интервала;
f m+1 частота следующего интервала.
Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой – больше.
Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми обладает половина единиц совокупности.
При определении медианы в интервальных вариационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Расчет медианы интервального вариационного ряда производится по формуле:
где х 0 нижняя граница интервала;
h – величина интервала;
f m частота интервала;
f – число членов ряда;
S m-1 – сумма накопленных членов ряда, предшествующих данному.
Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили и децили. Квартили делят ряд по сумме частот на четыре равные части, а децили – на десять равных частей. Квартилей насчитывается три, а децилей – девять.
Медиана и мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака и поэтому являются дополнительными и очень важными характеристиками статистической совокупности. На практике они часто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содержит некоторое количество единиц с очень большим или очень малым значением варьирующего признака.