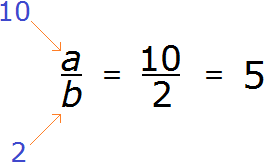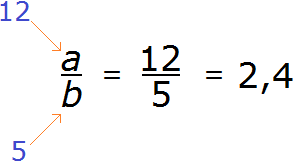что такое множество в математике 2 класс примеры правило
Что такое множество?
Множество — это набор каких-либо объектов. Объекты, из которых состоит множество, называются элементами этого множества.
В математике множество рассматривается намного шире. Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.
Обозначения
Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.
Обозначим множество наших друзей через заглавную латинскую букву F ( friends ), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:
Обозначим через любую заглавную латинскую букву данное множество, например, через букву D
затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6
Читается как «2 принадлежит множеству делителей числа 6»
Читается как «5 не принадлежит множеству делителей числа 6»
Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:
Зададим множество, которое состоит из одного числа 2
Зададим множество, которое состоит из двух чисел: 2 и 5
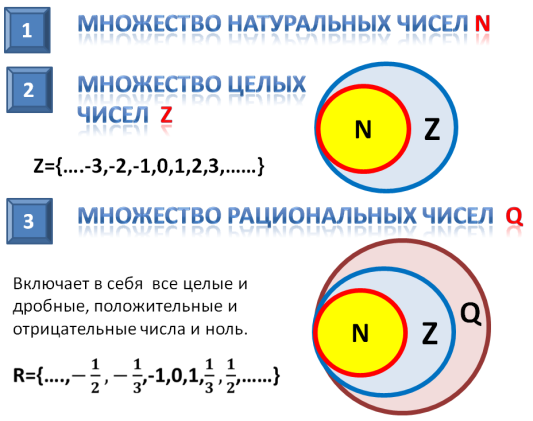
Множество натуральных чисел
Это первое множество с которым мы начали работать. Натуральными числами называют числа 1, 2, 3 и т.д.
Натуральные числа появились из-за потребности людей сосчитать те иные объекты. Например, посчитать количество кур, коров, лошадей. Натуральные числа возникают естественным образом при счёте.
В математике множество натуральных чисел обозначается заглавной латинской буквой N.
Например, укажем, что число 1 принадлежит множеству натуральных чисел. Для этого записываем число 1, затем с помощью знака принадлежности ∈ указываем, что единица принадлежит множеству N
Читается как: «единица принадлежит множеству натуральных чисел»
Множество целых чисел
Множество целых чисел включает в себя все положительные и отрицательные числа, а также число 0.
Укажем, к примеру, что число −5 принадлежит множеству целых чисел:
Укажем, что 10 принадлежит множеству целых чисел:
Укажем, что 0 принадлежит множеству целых чисел:
В будущем все положительные и отрицательные числа мы будем называть одним словосочетанием — целые числа.
Множество рациональных чисел
Рациональные числа, это те самые обыкновенные дроби, которые мы изучаем по сей день.
В роли числителя и знаменателя могут быть любые числа, в том числе и целые (за исключением нуля, поскольку на нуль делить нельзя).
Например, представим, что вместо a стоит число 10, а вместо b — число 2
10 разделить на 2 равно 5. Видим, что число 5 может быть представлено в виде дроби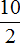 
, а значит число 5 входит во множество рациональных чисел.
Легко заметить, что число 5 также относится и ко множеству целых чисел. Стало быть множество целых чисел входит во множество рациональных чисел. А значит, во множество рациональных чисел входят не только обыкновенные дроби, но и целые числа вида −2, −1, 0, 1, 2.
Теперь представим, что вместо a стоит число 12, а вместо b — число 5.
12 разделить на 5 равно 2,4. Видим, что десятичная дробь 2,4 может быть представлена в виде дроби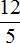 
, а значит она входит во множество рациональных чисел. Отсюда делаем вывод, что во множество рациональных чисел входят не только обыкновенные дроби и целые числа, но и десятичные дроби.
Мы вычислили дробь 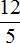и получили ответ 2,4. Но мы могли бы выделить в этой дроби целую часть:
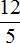
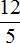
При выделении целой части в дроби , получается смешанное число 
. Видим, что смешанное число тоже может быть представлено в виде дроби . Значит во множество рациональных чисел входят и смешанные числа.
В итоге мы приходим к выводу, что множество рациональных чисел содержат в себе:
Множество рациональных чисел обозначается заглавной латинской буквой Q.
Например укажем, что дробь 
принадлежит множеству рациональных чисел. Для этого записываем саму дробь , затем с помощью знака принадлежности ∈ указываем, что дробь принадлежит множеству рациональных чисел:
∈ Q
Укажем, что десятичная дробь 4,5 принадлежит множеству рациональных чисел:
Укажем, что смешанное число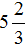 
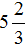
принадлежит множеству рациональных чисел:
∈ Q
Вводный урок по множествам завершён. В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
12 thoughts on “Что такое множество?”
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками < >.
А = <а, в, с, у>– А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N =
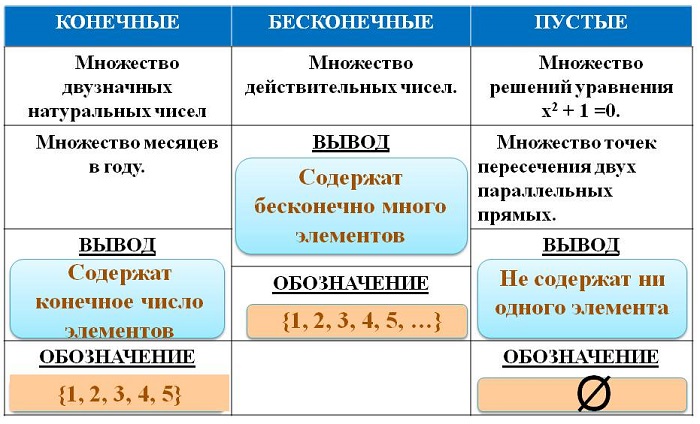
Выделяют три вида множеств:
пустые (обозначаются Ø) – не имеющие элементов.
Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Множество натуральных чисел
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
Следовательно, N и Z являются подмножествами Q.
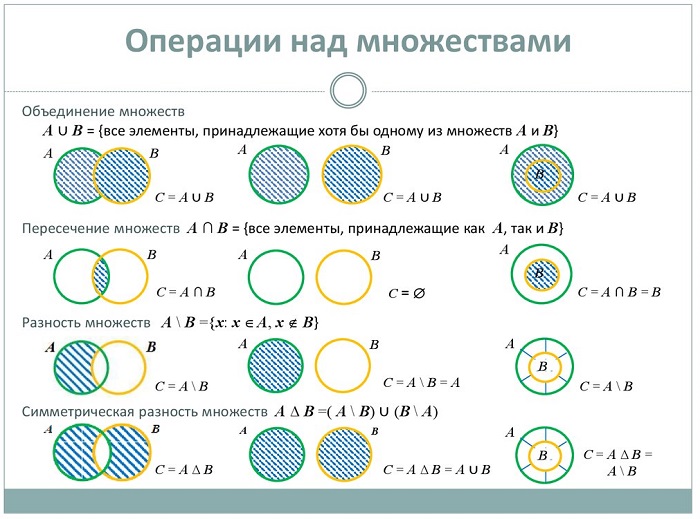
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
О других свойствах операций можно узнать из картинки:
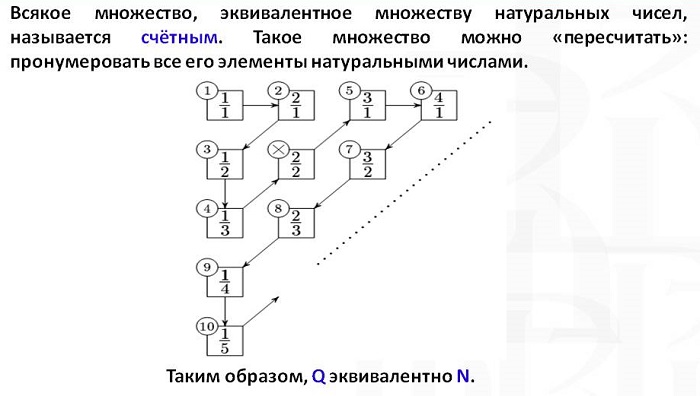
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Урок на тему «Множества» (2 класс)
создание условий для формирования у учащихся УУД
формирование ответственного отношения к учению на основе мотивации к обучению и познанию;
формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению;
через организацию работы в парах формировать навыки коллективной деятельности;
воспитание честной самооценки своей работы.
умение определять понятия, классифицировать элементы множеств, умение находить множества по определенным признакам и делать выводы;
развитие ИКТ– компетенции.
формирование представления об основных изучаемых понятиях: множества, элементы множеств
учебник «Информатика в играх и задачах» авт. Горячев
обучающая программа «множества»
карточки с заданиями
Урок создан в технологии развития критического мышления, использованы элементы здоровьесберегающие технологии.
I этап Фаза вызова.
Вызов уже имеющихся знаний по изучаемому вопросу, активизация учащихся, мотивация для дальнейшей работы.
Организационный момент
— со звонком учащиеся занимают свои места;
— отметить не пришедших на урок;
— объявить тему и цель урока.
Проверка домашнего задания :
Выяснить причину изменения формы брюк. Сделать выставку рисунков к рассказу. Побеседовать о том, в чем различия в рисунках и почему. (Каждый мог создать разный образ инопланетянина, выбрать разный цвет, форму, длину брюк, это зависит от фантазии, основанной на личном опыте.)
Вывод. Одна и та же исходная информация позволяет получить разнообразие конечные результаты
Актуализация:
— что такое информация?
— какую информацию мы получаем при просмотре картины?
— какой орган чувств помогает получать зрительную информацию?
II этап Осмысление.
Контакт с новой информацией. Работа ведется фронтально, индивидуально, в парах.
Возле елок и иголок
Летним днем построен дом.
За травой не виден он,
А жильцов в нем миллион!
— Что за дом и кто в нем живет? (муравейник с муравьями)
— Сколько муравьев в их домике? (миллион)
— Скажите об этом другими словами (много муравьев, множество муравьев)
— В жизни вам не раз приходилось слышать слово множество. Множество учеников в школе, множество книг в библиотеке, множество игрушек в детском саду. Назовите сами разные множества.
— Скажите, как вы думаете, что же такое множество?
— Можно сказать, что множество – это группа предметов или явлений, у которых есть что – то общее: признак, свойство, качество, действие или еще что –то.
— С какими множествами вам приходилось встречаться на уроках математики и русского языка? (множество чисел, множество геометрических фигур, множество букв, множество слов).
— Любое множество состоит из отдельных элементов. Перечислите элементы множеств:
Множество школьных предметов.
Учитель предлагает количество элементов какого-то множества. Ученик должен назвать эти элементы. Тот, кто назовет все элементы предложенного множества, становится ведущим. Например, ведущий: «Я знаю 5 имен девочек. », ученик: «Аня, Валя, Оля, Лена, Катя».
Игру можно упростить, учитель называет свое условие, дети по очереди дают ответы. Тот, чей ответ окажется последним, становится ведущим. Этот вариант приемлем для более сложных множеств, с точки зрения уровня знаний детей, например: множество планет, множество геометрических фигур, множество морей. Этот материал основан на личных, дополнительных знаниях детей, он опережает школьную программу данного возраста, поэтому предлагаются ответы нескольких учеников на один вопрос.
В процессе игры можно раздавать фишки за правильные ответы, чтобы выявить победителя.
Используя интерактивную доску необходимо выполнить задание:
Дать общее название множествам
Во время выполнения задания отрабатывается прием перетаскивания объектов на экране.
Самостоятельная работа (на месте)
Напиши названия множеств.
Окунь и карась – это ___________________
Метла и лопата – это ___________________
Лето и зима – это ______________________
Огурец и помидор – это ________________
Шкаф и диван – это ___________________
Июнь и июль – это ____________________
День и ночь – это _____________________
Дерево и цветок – это __________________
Выполни задание в парах:
«Дай название каждому множеству»
А теперь давайте отдохнем, мы ведь сделали так много:
– Встаньте множество мальчиков.
– Встаньте множество девочек.
– Помашите руками множество мальчиков, чьи имена начинаются на гласную букву.
– Покивайте головой множество девочек.
– Покружитесь на месте множество учеников 2 класса.
– Тихо сядьте множество мальчиков нашего класса.
– Тихо сядьте множество девочек нашего класса.
– Спойте песню множество бабушек этого класса.
Песню никто не спел. А почему? т.к. нет объектов у данного множества, в нашем классе нет бабушек. Такое множество называется пустым, а если мы знаем элементы-объекты множества, оно называется заданным. Еще есть бесконечное множество, например, множество звезд и др.
Ученики приводят примеры.
Прослушивание медиалекции «Множества», с помощью обучающей программы.
Работа за компьютером
Выполнить задание «Составь множество из соответствующих элементов». Предлагается создать 5 различных множеств из имеющихся элементов:
Множество живых существ;
Множество обитателей моря;
Множество неодушевленных предметов;
Множество овощей и фруктов;
Множество предметов, сделанных человеком.
Во время выполнения задания отрабатывается прием перетаскивания объектов на экране монитора с помощью мыши, совершенствуются навыки управления компьютерной программой.
III этап Рефлексия.
Подготовить и нарисовать примеры заданного и бесконечного множеств.
Что такое множество 👨🎓. Свойства и операции над множествами
В этой статье рассмотрим очень важную тему, как в математике, так и в информатике – множества. Ниже Вы найдете основные определения и понятия, свойства множеств, их виды и примеры. Материал изложен таким образом, что разберется даже полный чайник. Здесь приведены, только основы, которые обычно проходятся в рамках школьной программы. Читайте!
Основные положения и обозначения
Теория множеств появилась благодаря знаменитому немецкому математику Гео́рг Ка́нтор (3 марта 1845, Санкт-Петербург — 6 января 1918, Галле (Заале)) — немецкий математик, ученик Вейерштрасса. Наиболее известен как создатель теории множеств.
Итак, начнем с основных понятий. Основное определение имеет следующий вид:
Множества (м-ва – сокр.) – наборы элементов объединенных по какому либо признаку.
Обозначаются они с помощью заглавных латинских букв, а их элементы указываются в фигурных скобках.
Примеры
\( S = \left\ < а, б, в, г, д, …, ю, я \right\>\) – мн-во букв русского алфавита.
\( S = \left\ < Алексей, Анатолий, Галина, …, Александр, Ирина \right\>\) – мн-во имен студентов в группе.
\( S = \left\ < 🐵, 🙈, 🙉, 🙊 \right\>\) – мн-во смайликов с изображением обезьянок.
Также стоит обговорить про принадлежность элементов к множеству. Записать её можно с помощью специального значка «принадлежности» – \( \in \) . Так запись вида \( x \in S \) обозначает, что элемент x принадлежит множеству S.
С основным понятием разобрались, перейдем к остальной теории.
Подмножества
Подмножество – множество S1 является подмножеством S, если каждый элемент из S1 содержится (включен) в S.
Обозначают подмножества при помощи специального значка «включения», который имеет вид \( \subset \) \( (\ S_1 \subset S \ ) \) . Также их можно отобразить схематично, используя диаграммы Эйлера, которые отображают отношения между подмножествами.
Также Вы можете выделить подмножество мужских имен, или сделать любую выборку по какому-нибудь признаку.
Мощность
Следует также выделить такое понятие, как мощность. Имеет оно следующий вид:
Мощность – количество элементов, которое содержится в множестве.
Мн-ва называются равномощными тогда и только тогда, когда количество элементов одного из них равно количеству элементов другого.
Причем неважно, какие элементы будут в этих мн-ах. Так в одном из них могут содержаться 26 букв английского алфавита, а в другом 26 марок японских автомобилей, при этом они будут равномощными.
Мощность является одним из тех свойств, благодаря которому мы можем проводить сравнение двух (или более) м-в.
Равенство
Необходимо сказать и про равенство. Для чайников правило будет выглядеть так:
Два (или несколько) множеств равны только тогда, когда равны все их элементы.
Теперь изучим виды и другие свойства мн-в в математике.
Существует много критериев и свойств, по которым мы можем классифицировать множества. Например, мы можем разделить их по количеству элементов:
А можем поделить их на конечные (ограниченные) и бесконечные:
Теперь рассмотрим примеры множеств в математике.
Примеры
Натуральные числа
Натуральные числа в математике – это те числа, которые мы используем при счете (1, 2, 3 и т.д.). Сюда не относятся отрицательные величины и нуль. Запись: \( N = \left\ < 1, 2, 3, 4, 5, … \right\>\).
Целые числа
Получаются из множества натуральных чисел. К ним добавляются отрицательные числа и нуль. \( Z = \left\ < 0, \pm 1, \pm 2, \pm 3, \pm 4, \pm 5, … \right\>\).
Рациональные числа
Здесь множество задается следующим образом: \( Q = \left\ <
Так как любое число в математике можно представить в виде дроби (например, \( 5 = <5 \over 1>\) ), то целые числа являются подмножеством рациональных чисел. Натуральные же числа являются подмножеством целых чисел.
\[ N \subset Z \subset Q \]
Эту теорию Вам надо запомнить.
Операции
В этом разделе рассмотрим основные операции (действия) над множествами в математике.
Пересечение
Чтобы поняли даже чайники, вернемся к нашим «мартышкам»:
\( S_ <1>= \left\ < 🙉, 🙊 \right\>\) — обезьянки показывающие лапки и глаза
\( S_ <2>= \left\ < 🙈, 🙉 \right\>\) — мартышки показывающие лапы и рот
Надо найти \( S_ <1>\ \cap \ S_ <2>\). Для этого воспользуемся диаграммами Эйлера — Венна:
Решение: \( S_ <1>\ \cap \ S_ <2>= \left\ < 🙉 \right\>\) т.к. 🙉 входит и в S1 и в S2.
Объединение
Решение: \( S_ <1>\ \cup \ S_ <2>= \left\ < 🙈, 🙉, 🙊 \right\>\)
Разность
Решение: \( S_ <1>\ \setminus \ S_ <2>= \left\ < 🙊 \right\>\)
Следует отметить, что здесь приведены не все операции. Например, не написано про симметрическую разность и законы Моргана. Их проходят в рамках высшей математики.
Заключение
Теперь Вы знаете, что такое мн-ва, знаете их свойства и какие операции над ними можно выполнять. Надеюсь я объяснил всю теорию так, что понял даже полный чайник. Если же у Вас возникли вопросы, то задавайте их в комментариях. Также на нашем сайте Вы можете прочитать другие статьи, например про представления чисел в компьютере. Рассказывается как выполнять с ними такие действия, как перемножение, получение суммы и деление.