что такое многозначные числа
Многозначные числа. Состав числа. Сравнение чисел.
Многозначные числа
Число называют однозначным, если его запись состоит из одного знака — одной цифры.
Например, числа 3, 7, 9 — однозначные.
Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным.
Например, числа 25, 44, 65, 80 — двузначные.
Числа 100, 543, 888 — трёхзначные:
Числа 2000, 6791, 1060 — четырёхзначные и т. д.
Двузначные, трехзначные, четырёхзначные, пятизначные и т. д. — это многозначные числа.
Место, занимаемое цифрой в записи числа, называют разрядом.
Если в числа отсутствуют единицы какого-либо разряда, то на месте этого разряда в записи числа ставят цифру 0. Например, триста восемь записывают так:
Любое число, имеющее разряды, можно разложить на сумму разрядных слагаемых.
303 = 3 • 100 + 0 • 10 + 3
998 = 9 • 100 + 9 • 10 + 8
Сравнение чисел
Числа можно сравнить так:
1) по месту, которое они занимают при счёте.
7 456, так как 7 дес. > 5 дес.
Поделись с друзьями в социальных сетях:
Что такое многозначные числа
ПРОЯСНЯЙ СЛОВА: МАТЕМАТИКА!
«Если бы мы немного лучше знали и понимали вещи,
то мы все жили бы более счастливо».
Здравствуйте, дорогие читатели!
Бесспорно, математика – одна из важнейших наук. Поэтому известный итальянский ученый Галилео Галилей утверждал, что «великая книга природы написана математическими символами». Но невозможно усвоить какую-то науку, не зная основ; а зная их, обучение превращается в захватывающее и интригующее исследование.
Поэтому сегодня мы возьмем новое слово из основ математики, и проясним его. «Прояснить» значит «сделать для себя ясным и понятным что-то». И сегодняшнее выражение, которое мы будем прояснять, это – МНОГОЗНАЧНЫЕ ЧИСЛА.
ОПРЕДЕЛЕНИЕ ВЫРАЖЕНИЯ МНОГОЗНАЧНЫЕ ЧИСЛА (ДЕФИНИЦИЯ)
МНОГОЗНАЧНЫЕ ЧИСЛА – это такие целые числа, при записи которых нужно использовать несколько цифр (знаков).
Например, числа 2 и 3 – это ОДНОЗНАЧНЫЕ числа, так как для их записи нужно всего по одной цифре (то есть по одному знаку). А вот числа 22, 257 или 3 561 – это МНОГОЗНАЧНЫЕ числа, так как для записи этих чисел необходимо использовать более одной цифры.
Числа, для записи которых необходимо использовать 2 цифры (два знака), называют ДВУЗНАЧНЫМИ.
Числа, для записи которых необходимо использовать 3 цифры (три знака), называют ТРЕХЗНАЧНЫМИ, и так далее.
Интересно! Сейчас в школах таблицу умножения учат до двенадцати, но раньше ее учили до девяти. Посмотрите картинку:
В ней учили умножать только ОДНОЗНАЧНЫЕ числа. А вот МНОГОЗНАЧНЫЕ числа обычно умножают «в столбик».
Внимание, конкурс! Сколько-значное получится число, если перемножить все однозначные числа натурального ряда? Присылайте свой ответ нам и выиграйте приз!
А теперь прочитайте предложения с выражением МНОГОЗНАЧНЫЕ ЧИСЛА, чтобы разобраться с тем, как можно использовать это слово в своей речи:
ПРОИСХОЖДЕНИЕ ВЫРАЖЕНИЯ МНОГОЗНАЧНЫЕ ЧИСЛА (ЭТИМОЛОГИЯ)
Чтобы лучше понять это выражение, стоит попробовать разобраться с его происхождением. Итак, смотрим:
Слово МНОГОЗНАЧНЫЙ, то есть «много знаков», происходит от слова znati, что на одном из славянских языков означало «отличать, заметить».
Слово ЧИСЛО происходит от слова суsɫо, что на одном из славянских языков так и означало «число».
НЕСКОЛЬКО СЛОВ В ЗАКЛЮЧЕНИЕ
Проясняйте математические термины и не пропускайте наши выпуски!
ПОДПИШИТЕСЬ НА ОСТАЛЬНЫЕ НАШИ
РАССЫЛКИ ПО ПРОЯСНЕНИЮ СЛОВ:
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
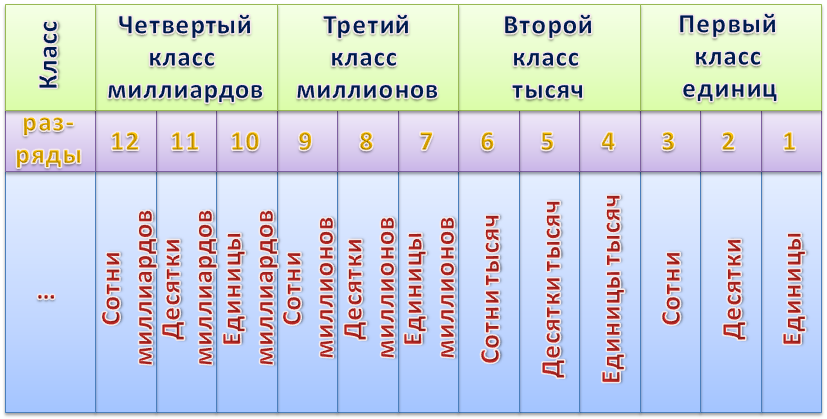
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
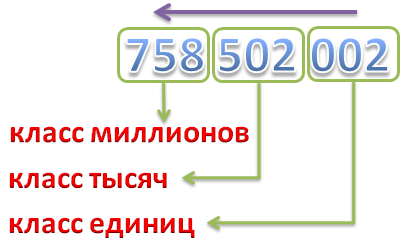
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отброс ить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
интернет проект BeginnerSchool.ru
Сайт для детей и их родителей
Многозначные числа
В прошлый раз мы говорили о цифрах и о разрядах. Продолжим тему и разберем, что такое классы.
Для чего же нам может понадобиться знание о классах. Многозначные числа разбивают на классы для удобства их чтения и записи.
Классы
Все разряды можно сгруппировать в отдельные классы, которые, как и разряды, считают справа налево.
Каждые три разряда образуют класс:
Таблицу разрядов можно преобразовать в таблицу классов следующим образом:
К первому классу « Единиц » относятся следующие разряды: единицы, десятки и сотни.
Ко второму классу « Тысяч » относятся разряды единиц, десятков и сотен тысяч.
К третьему классу « Миллионов » относятся разряды единиц, десятков и сотен миллионов.
К четвертому классу « Миллиардов » или «Биллионов» относятся разряды единиц, десятков и сотен миллиардов.
Эта таблица неполная. Далее за классом миллиардов идет пятый класс триллионов со своими единицами, десятками и сотнями и так далее.
Сделаем вывод, все классы имеют одинаковые черты, а именно:
• в каждом классе по три разряда;
• десять единиц одного разряда, каждого класса, образуют одну единицу следующего разряда;
• тысяча единиц одного класса образуют одну единицу следующего класса.
Называя разряды классов, произносят и имя класса, всех кроме первого (смотри таблицу).
Например: десятки тысяч, сотни миллионов, единицы миллиардов. Называя разряды первого класса, произнося только имя разряда без имени класса: единицы, десятки, сотни.
Давайте рассмотрим несколько примеров:
1. 70 000 – семь десятков тысяч.
2. 400 000 – четыре сотни тысяч.
3. 600 – шесть сотен.
Чтение многозначных чисел
Для чтения многозначных чисел:
1. Разбиваем многозначное число на классы, по 3 разряда в каждом. Числа на классы разбиваются справа налево, то есть, начинаем с конца числа:
2. Определяем названия классов:
3. Называем числа объединенные классом, начиная со старшего класса, слева направо, произнося в конце название класса:
4. Продолжаем читать последовательно все названия классов. Если в разряде класса записаны нули, то этот разряд не читают. Название последнего класса не произносят.
Запись многозначных чисел
Записывая такое число, нам надо помнить следующие правила:
Итак, запишем наше число:
сорок миллионов четыре тысячи восемьсот пятьдесят три – 40 004 853
Другой пример, в котором отсутствует целый класс:
пять миллионов четыре – 5 000 004
Спасибо, что Вы с нами!
Оставляйте пожалуйста комментарии в форме ниже
Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.
Многозначные числа.
Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.
Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.
Разряды чисел.
Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.
Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.
Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.
Такой разбор числа называется разрядным составом числа.
Классы.
Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.
Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.
Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.
Таблица разрядов и классов.
Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891 и прочитать число единиц каждого класса слева направо:

Сумма разрядных слагаемых.
Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.
4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать
4062=4 ⋅1000+0 ⋅100+6 ⋅10+2
Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0
Вопросы по теме:
Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.
Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.
Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.
Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.
Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.
Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)
Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)
Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.
Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.
Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)
Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)
Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.
Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.
Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6