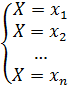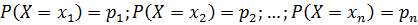что такое многоугольник распределения
2.2.6. Многоугольник распределения
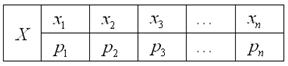
Итак, пусть дискретная случайная величина 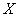
Многоугольником распределения вероятностей данной величины называют ломаную, звенья которой соединяют соседние точки 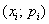
Задача 91
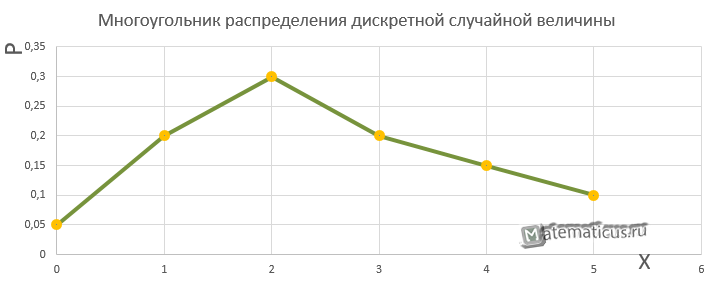
Построить многоугольник распределения вероятностей случайной величины
Решение: чертим прямоугольную систему координат, в которой по оси абсцисс отсчитываются 
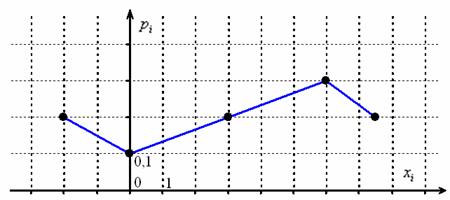
При выполнении чертежа от руки по возможности придерживайтесь следующего масштаба:
горизонтальная ось: 1 ед. = 2 тетрадные клетки (1 см);
вертикальная ось: 0,1 = 2 тетрадные клетки.
Если значения 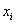
Теперь обратите внимание на следующую важную вещь: помимо того, что дискретную случайную величину можно изобразить с помощью многоугольника – её ведь можно ещё и ЗАДАТЬ этим способом. До сих пор мы делали это с помощью таблички, но никто же не мешает использовать и чертёж!
Задача 92
Дискретная случайная величина 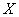
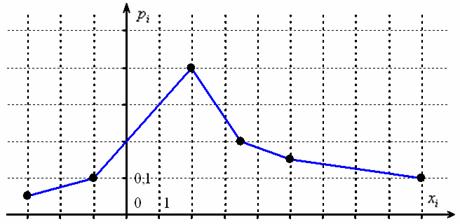
Записать закон распределения данной случайной величины, выполнить проверку.
Это задание для самостоятельного решения. И тут мы, кстати, видим изъян графического способа: по чертежу не всегда понятны точные значения случайной величины и их вероятности.
На практике задачи с многоугольником встречаются довольно часто, но гораздо бОльшее распространение получила:
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Многоугольник распределения дискретной случайной величины
Многоугольник распределения является одной из форм закона распределения случайной величины.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| p | 0.05 | 0.2 | 0.3 | 0.2 | 0.15 | 0.1 |
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.2 / 5. Количество оценок: 5
Ряд распределения. Многоугольник распределения.



Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, не известное заранее. Случайные величины бывают прерывного (дискретного) и непрерывного типа. Возможные значения прерывных величин заранее могут быть перечислены. Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Пример дискретных случайных величин:
1) Число появления герба при трех бросаниях монеты. (возможны значения 0;1;2;3)
2) Частота появления герба в том же опыте. (возможные значения 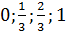
3) Число отказавших элементов в приборе, состоящем из пяти элементов. (Возможные значения величин 0;1;2;3;4;5)
Примеры непрерывных случайных величин:
1) Абсцисса (ордината) точки попадания при выстреле.
2) Расстояние от точки попадания до центра мишени.
3) Время безотказной работы прибора (радиолампы).
Случайны величины обозначаются большими буквами, а их возможные значения – соответствующими малыми буквами. Например, X – число попаданий при трех выстрелах; возможные значения: X1=0,Х2=1, Х3=2, Х4=3.
Обозначим вероятности этих событий буквами p с соответствующими индексами:
Так как несовместные события образуют полную группу, то

то есть сумма вероятности всех возможных значений случайной величины равна 1. Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, то есть в точности укажем какой вероятностью обладает каждое из событий. (Этим мы установим так называемый закон распределения случайных величин.)
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующей им вероятности. (Про случайную величину мы будем говорить, что она подчинена данному закону распределения)
Простейшей формой задания закона распределения случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
| Xi | X1 | X2 | … | Xn |
| Pi | P1 | P2 | … | Pn |
Такую таблицу называют рядом распределения случайных величин.
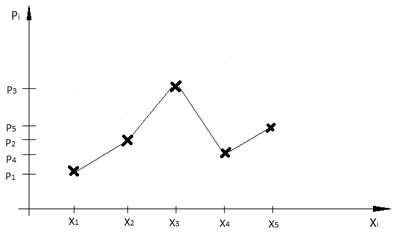
Чтобы придать ряду распределения более наглядный вид прибегают к его графическому изображению: по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – вероятности этих значений. (Для наглядности полученные точки соединяют отрезками прямых.)
Рисунок 1 – многоугольник распределения
Такая фигура называется многоугольником распределения. Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину; он является одной из форм закона распределения.
производится один опыт, в котором может появиться или не появиться событие А. Вероятность события А=0,3. Рассматривается случайная величина Х – число появлений события А в данном опыте. Необходимо построить ряд и многоугольник распределения величины Х.
Функция распределения является универсальной характеристикой случайной величины. Она существует для всех случайных величин: как прерывных, так и не прерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, то есть является одной из форм закона распределения.
Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события X=x, а вероятностью события X