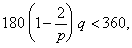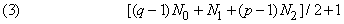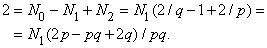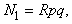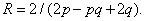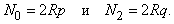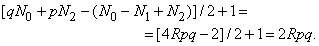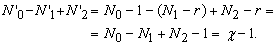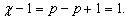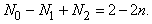что такое многогранник определение
Что такое многогранник? Примеры
Примеры многогранников:
1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.
Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.
Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.
Популярное
В этой статье мы познакомим вас с технологиями изготовления геометрических тел из металла, которые применяет мастер Иван Кочкин.
Если ты не любишь математику, опасайся хэллоуина! Злые силы придут за тобой в хэллоуин! Создай двух стражей, которые будут оберегать тебя от злых сил! Ну, или.
Александрийский маяк — одно из 7 чудес света, был построен в III веке до н. э. в египетском городе Александрия, чтобы корабли могли благополучно миновать рифы на пути в александрийскую.
Можно ли представить икосаэдр в виде более простых многогранников.
Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира.
Нам нужны еще фонарики Джека в форме тыквы. Кто же нам поможет? Может быть Архимед?
Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон? Одним лишь вращением мы можем.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 13. Многогранники
Перечень вопросов, рассматриваемых в теме:
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.
Грани многогранника – многоугольники, ограничивающие многогранники.
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника (вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.
Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)
Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)
Открытые электронные ресурсы:
Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.
Теоретический материал для самостоятельного изучения
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.
Б)
Рисунок 1 – разные подходы к определению многоугольника
Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.
В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)
Рисунок 2 – изображение октаэдра
Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).
Рисунок 3 – Виды многогранников
Сумма плоских углов при вершине выпуклого многогранника
Рисунок 4 – сумма плоских углов пи вершине многогранника
Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.
Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.
Задание 2. Сопоставьте геометрическим фигурам их вид
Б) пространственная фигура
Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б
многогранник
Смотреть что такое «многогранник» в других словарях:
многогранник — многогранник … Орфографический словарь-справочник
МНОГОГРАННИК — геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер вершинами многогранника. По числу граней различают четырехгранники, пятигранники и т.… … Большой Энциклопедический словарь
многогранник — полиэдр, политоп; симплекс Словарь русских синонимов. многогранник сущ. • полиэдр Словарь русских синонимов. Контекст 5.0 Информатик. 2012 … Словарь синонимов
МНОГОГРАННИК — МНОГОГРАННИК, многогранника, муж. (мат.). Геометрическое тело, ограниченное со всех сторон плоскими прямолинейными гранями (треугольниками, четырехугольниками и т.д.). Правильный многогранник. || Такое же тело, ограниченное более, чем четырьмя… … Толковый словарь Ушакова
МНОГОГРАННИК — МНОГОГРАННИК, а, муж. Геометрическое тело, ограниченное со всех сторон плоскими многоугольниками. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Многогранник — [polihedron] выпуклое ограниченное множество точек, удовлетворяющих одновременно конечному числу неравенств типа: a11x1 + … + a1nxn ≤ b1 ……………….. am1x1 + … + amnxn ≤ bm или в матричной записи M =… … Экономико-математический словарь
МНОГОГРАННИК — (полиэдр) геометрическое тело, ограниченное плоскими (см.). Правильный М. геометрическая выпуклая поверхность, у которой все грани правильные многоугольники с одним и тем же числом сторон и в каждой вершине многогранника сходится одинаковое… … Большая политехническая энциклопедия
МНОГОГРАННИК — часть пространства, ограниченная совокупностью конечного числа плоских многоугольников (см. ГЕОМЕТРИЯ), соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого… … Энциклопедия Кольера
Многогранник — В Викисловаре есть статья «многогранник» … Википедия
Многогранник
Многогранник или полиэдр — обычно замкнутая поверхность, составленная из многоугольников, но иногда также называют тело ограниченное этой поверхностью.
Содержание
Определение
Многогранник, точнее трёхмерный многогранник — совокупность конечного числа плоских многоугольников в трёхмерном евклидовом пространстве такая, что:
Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника. Простейшими примерами многогранников являются выпуклые многогранники, то есть граница ограниченного подмножества евклидова пространства являющееся пересечением конечного числа полупространств.
Варианты значения
Приведенное определение многогранника получает различный смысл в зависимости от того, как определить многоугольник, для которого возможны следующие два варианта:
В первом случае мы получаем понятие звёздчатый многогранник. Во втором — многогранник есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность некоторого геометрического тела, которое также называется многогранником. Отсюда возникает третье определение многогранника, как самого геометрического тела.
Связанные определения
Выпуклый многогранник
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней.
Вариации и обобщения
Примечания
См. также
Ссылки
Полезное
Смотреть что такое «Многогранник» в других словарях:
многогранник — многогранник … Орфографический словарь-справочник
МНОГОГРАННИК — геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер вершинами многогранника. По числу граней различают четырехгранники, пятигранники и т.… … Большой Энциклопедический словарь
многогранник — полиэдр, политоп; симплекс Словарь русских синонимов. многогранник сущ. • полиэдр Словарь русских синонимов. Контекст 5.0 Информатик. 2012 … Словарь синонимов
МНОГОГРАННИК — МНОГОГРАННИК, многогранника, муж. (мат.). Геометрическое тело, ограниченное со всех сторон плоскими прямолинейными гранями (треугольниками, четырехугольниками и т.д.). Правильный многогранник. || Такое же тело, ограниченное более, чем четырьмя… … Толковый словарь Ушакова
МНОГОГРАННИК — МНОГОГРАННИК, а, муж. Геометрическое тело, ограниченное со всех сторон плоскими многоугольниками. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Многогранник — [polihedron] выпуклое ограниченное множество точек, удовлетворяющих одновременно конечному числу неравенств типа: a11x1 + … + a1nxn ≤ b1 ……………….. am1x1 + … + amnxn ≤ bm или в матричной записи M =… … Экономико-математический словарь
МНОГОГРАННИК — (полиэдр) геометрическое тело, ограниченное плоскими (см.). Правильный М. геометрическая выпуклая поверхность, у которой все грани правильные многоугольники с одним и тем же числом сторон и в каждой вершине многогранника сходится одинаковое… … Большая политехническая энциклопедия
МНОГОГРАННИК — часть пространства, ограниченная совокупностью конечного числа плоских многоугольников (см. ГЕОМЕТРИЯ), соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого… … Энциклопедия Кольера
многогранник — а; м. Геометрическое тело, ограниченное со всех сторон плоскими многоугольниками. Правильный м. * * * многогранник геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются рёбрами… … Энциклопедический словарь
МНОГОГРАННИК
МНОГОГРАННИК, часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников. Эти многоугольники называются гранями, их стороны – ребрами, а вершины – вершинами многогранника.
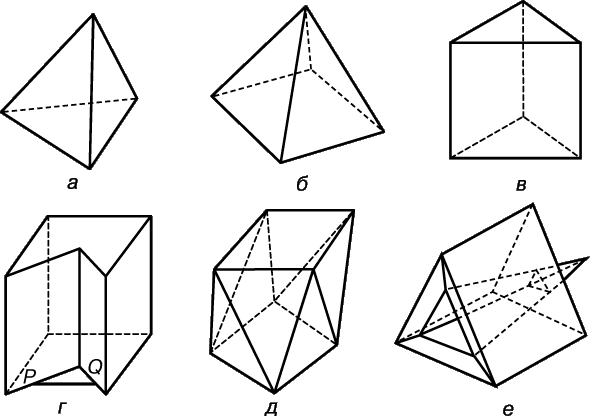
На рис. 1 представлены несколько известных многогранников. Первые два служат примерами р-угольных пирамид, т.е. многогранников, состоящих из р-угольника, называемого основанием, и р треугольников, примыкающих к основанию и имеющих общую вершину (называемую вершиной пирамиды). При р = 3 (см. рис. 1,а) основанием может служить любая грань пирамиды. Пирамида, основание которой имеет форму правильного р-угольника, называется правильной р-угольной пирамидой. Так, можно говорить о квадратных, правильных пятиугольных и т.д. пирамидах. На рис. 1,в, 1,г и 1,д приведены примеры некоторого класса многогранников, вершины которых можно разделить на два множества из одинакового числа точек; точки каждого из этих множеств являются вершинами р-угольника, причем плоскости обоих p-угольников параллельны. Если эти два р-угольника (основания) конгруэнтны и расположены так, что вершины одного р-угольника соединены с вершинами другого р-угольника параллельными прямолинейными отрезками, то такой многогранник называется р-угольной призмой. Примерами двух р-угольных призм могут служить треугольная призма (р = 3) на рис. 1,в и пятиугольная призма (р = 5) на рис. 1,г. Если же основания расположены так, что вершины одного р-угольника соединены с вершинами другого р-угольника зигзагообразной ломаной, состоящей из 2р прямолинейных отрезков, как на рис. 1,д, то такой многогранник называется р-угольной антипризмой.
Кроме двух оснований, у р-угольной призмы имеются р граней – параллелограммов. Если параллелограммы имеют форму прямоугольников, то призма называется прямой, а если к тому же основаниями служат правильные р-угольники, то призма называется прямой правильной р-угольной призмой. р-угольная антипризма имеет (2p + 2) граней: 2р треугольных граней и два p-угольных основания. Если основаниями служат конгруэнтные правильные р-угольники, а прямая, соединяющая их центры, перпендикулярна их плоскостям, то антипризма называется прямой правильной р-угольной антипризмой.
В определении многогранника последняя оговорка сделана для того, чтобы исключить из рассмотрения такие аномалии, как две пирамиды с общей вершиной. Теперь мы введем дополнительное ограничение множества допустимых многогранников, потребовав, чтобы никакие две грани не пересекались, как на рис. 1,е. Любой многогранник, удовлетворяющий этому требованию, делит пространство на две части, одна из которых конечна и называется «внутренней». Другая, оставшаяся часть, называется внешней.
Многогранник называется выпуклым, если ни один прямолинейный отрезок, соединяющий любые две его точки, не содержит точек, принадлежащих внешнему пространству. Многогранники на рис. 1,а, 1,б, 1,в и 1,д выпуклые, а пятиугольная призма на рис. 1,г не выпуклая, так как, например, отрезок PQ содержит точки, лежащие во внешнем пространстве призмы.
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если он удовлетворяет следующим двум условиям:
-283(i) все его грани – конгруэнтные правильные многоугольники;
(ii) к каждой вершине примыкает одно и то же число граней.
Если все грани – правильные р-угольники и q из них примыкают к каждой вершине, то такой правильный многогранник обозначается <p, q>. Это обозначение было предложено Л.Шлефли (1814–1895), швейцарским математиком, которому принадлежит немало изящных результатов в геометрии и математическом анализе.
Существуют невыпуклые многогранники, у которых грани пересекаются и которые называются «правильными звездчатыми многогранниками». Так как мы условились такие многогранники не рассматривать, то под правильными многогранниками мы будем понимать исключительно выпуклые правильные многогранники.
Платоновы тела.
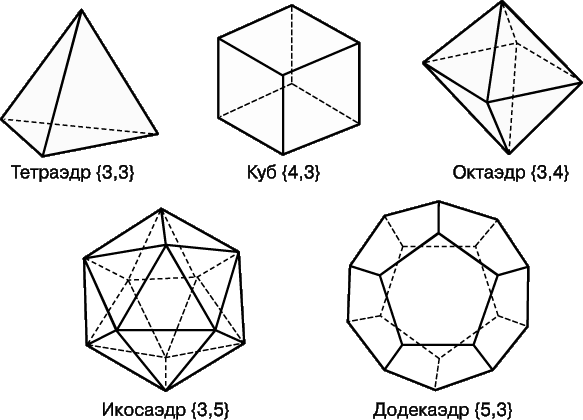
На рис. 2 изображены правильные многогранники. Простейшим из них является правильный тетраэдр, гранями которого служат четыре равносторонних треугольника и к каждой из вершин примыкают по три грани. Тетраэдру соответствует запись <3, 3>. Это не что иное, как частный случай треугольной пирамиды. Наиболее известен из правильных многогранников куб (иногда называемый правильным гексаэдром) – прямая квадратная призма, все шесть граней которой – квадраты. Так как к каждой вершине примыкают по 3 квадрата, куб обозначается <4, 3>. Если две конгруэнтные квадратные пирамиды с гранями, имеющими форму равносторонних треугольников, совместить основаниями, то получится многогранник, называемый правильным октаэдром. Он ограничен восемью равносторонними треугольниками, к каждой из вершин примыкают по четыре треугольника, и следовательно, ему соответствует запись <3, 4>. Правильный октаэдр можно рассматривать и как частный случай прямой правильной треугольной антипризмы. Рассмотрим теперь прямую правильную пятиугольную антипризму, грани которой имеют форму равносторонних треугольников, и две правильные пятиугольные пирамиды, основания которых конгруэнтны основанию антипризмы, а грани имеют форму равносторонних треугольников. Если эти пирамиды присоединить к антипризме, совместив их основания, то получится еще один правильный многогранник. Двадцать его граней имеют форму равносторонних треугольников, к каждой вершине примыкают по пять граней. Такой многогранник называется правильным икосаэдром и обозначается <3, 5>. Помимо четырех названных выше правильных многогранников, существует еще один – правильный додекаэдр, ограниченный двенадцатью пятиугольными гранями; к каждой его вершине примыкают по три грани, поэтому додекаэдр обозначается как <5, 3>.
Пять перечисленных выше правильных многогранников, часто называемых также «телами Платона», захватили воображение математиков, мистиков и философов древности более двух тысяч лет назад. Древние греки даже установили мистическое соответствие между тетраэдром, кубом, октаэдром и икосаэдром и четырьмя природными началами – огнем, землей, воздухом и водой. Что касается пятого правильного многогранника, додекаэдра, то они рассматривали его как форму Вселенной. Эти идеи не являются одним лишь достоянием прошлого. И сейчас, спустя два тысячелетия, многих привлекает лежащее в их основе эстетическое начало. О том, что они не утратили свою притягательность и поныне, весьма убедительно свидетельствует картина испанского художника Сальвадора Дали Тайная вечеря.
Древними греками исследовались также и многие геометрические свойства платоновых тел; с плодами их изысканий можно ознакомиться по 13-й книге Начал Евклида. Изучение платоновых тел и связанных с ними фигур продолжается и поныне. И хотя основными мотивами современных исследований служат красота и симметрия, они имеют также и некоторое научное значение, особенно в кристаллографии. Кристаллы поваренной соли, тиоантимонида натрия и хромовых квасцов встречаются в природе в виде куба, тетраэдра и октаэдра соответственно. Икосаэдр и додекаэдр среди кристаллических форм не встречаются, но их можно наблюдать среди форм микроскопических морских организмов, известных под названием радиолярий.
Число правильных многогранников.
Естественно спросить, существуют ли кроме платоновых тел другие правильные многогранники. Как показывают следующие простые соображения, ответ должен быть отрицательным. Пусть <p, q> – произвольный правильный многогранник. Так как его гранями служат правильные р-угольники, их внутренние углы, как нетрудно показать, равны (180 – 360/р) или 180 (1 – 2/р) градусам. Так как многогранник <p, q> выпуклый, сумма всех внутренних углов по граням, примыкающим к любой из его вершин, должна быть меньше 360 градусов. Но к каждой вершине примыкают q граней, поэтому должно выполняться неравенство
где символ 5 допустимых значений q не существует. Следовательно, других правильных многогранников, кроме тел Платона, не существует.
Все пять правильных многогранников перечислены в таблице, приведенной ниже. В трех последних столбцах указаны N0 – число вершин, N1 – число ребер и N2 – число граней каждого многогранника.
К сожалению, приводимое во многих учебниках геометрии определение правильного многогранника неполно. Распространенная ошибка состоит в том, что в определении требуется лишь выполнение приведенного выше условия (i), но упускается из виду условие (ii). Между тем условие (ii) совершенно необходимо, в чем проще всего убедиться, рассмотрев выпуклый многогранник, удовлетворяющий условию (i), но не удовлетворяющий условию (ii). Простейший пример такого рода можно построить, отождествив грань правильного тетраэдра с гранью еще одного тетраэдра, конгруэнтного первому. В результате мы получим выпуклый многогранник, шестью гранями которого являются конгруэнтные равносторонние треугольники. Однако к одним вершинам примыкают три грани, а к другим – четыре, что нарушает условие (ii).
ПЯТЬ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
Свойства правильных многогранников.
Вершины любого правильного многогранника лежат на сфере (что вряд ли вызовет удивление, если вспомнить, что вершины любого правильного многоугольника лежат на окружности). Помимо этой сферы, называемой «описанной сферой», имеются еще две важные сферы. Одна из них, «срединная сфера», проходит через середины всех ребер, а другая, «вписанная сфера», касается всех граней в их центрах. Все три сферы имеют общий центр, который называется центром многогранника.
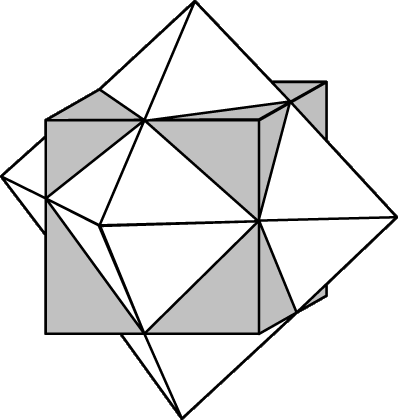
Двойственные многогранники.
Рассмотрим правильный многогранник <p, q> и его срединную сферу S. Средняя точка каждого ребра касается сферы. Заменяя каждое ребро отрезком перпендикулярной прямой, касательной к S в той же точке, мы получим N1 ребер многогранника, двойственного многограннику <p, q>. Нетрудно показать, что гранями двойственного многогранника служат правильные q-угольники и что к каждой вершине примыкают р граней. Следовательно, многограннику <p, q> двойствен правильный многогранник <q, p>. Многограннику <3, 3>двойствен другой многогранник <3, 3>, конгруэнтный исходному (поэтому <3, 3>называется самодвойственным многогранником), многограннику <4, 3>двойствен многогранник <3, 4>, а многограннику <5, 3>– многогранник <3, 5>. На рис. 3 многогранники <4, 3>и <3, 4>показаны в положении двойственности друг другу. Кроме того, каждой вершине, каждому ребру и каждой грани многогранника <p, q> соответствует единственная грань, единственное ребро и единственная вершина двойственного многогранника <q, p>. Следовательно, если <p, q> имеет N0 вершин, N1 ребер и N2 граней, то <q, p> имеет N2 вершин, N1 ребер и N0 граней.
Так как каждая из N2 граней правильного многогранника <p, q> ограничена р ребрами и каждое ребро является общим ровно для двух граней, то всего имеется pN2/2 ребер, поэтому N1 = pN2/2. У двойственного многогранника <q, p> ребер также N1 и N0 граней, поэтому N1 = qN0/2. Таким образом, числа N0, N1 и N2 для любого правильного многогранника <p, q> связаны соотношением
Симметрия.
Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают. Под симметрией (или преобразованием симметрии) многогранника мы понимаем такое его движение как твердого тела в пространстве (например, поворот вокруг некоторой прямой, отражение относительно некоторой плоскости и т.д.), которое оставляет неизменными множества вершин, ребер и граней многогранника. Иначе говоря, под действием преобразования симметрии вершина, ребро или грань либо сохраняет свое исходное положение, либо переводится в исходное положение другой вершины, другого ребра или другой грани.
Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника как твердого тела здесь понимается выполнение отдельных движений в определенном заранее установленном порядке. Например, упоминавшийся выше поворот на угол 360/р градусов вокруг прямой l есть произведение отражений относительно любых двух плоскостей, содержащих l и образующих относительно друг друга угол в 180/р градусов. Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким образом, любой поворот вокруг прямой – прямая симметрия. Любое отражение есть обратная симметрия.
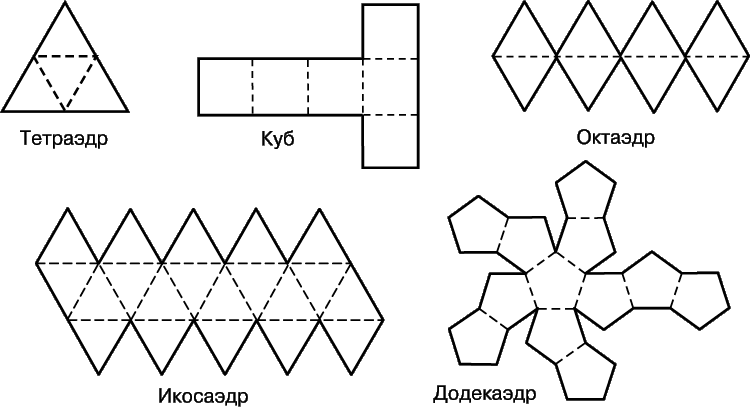
Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника <3, 3>. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра. Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии. Для наглядности полезно построить картонную модель правильного тетраэдра и убедиться, что тетраэдр действительно обладает 24 симметриями. Развертки, которые можно вырезать из тонкого картона и, сложив, склеить из них пять правильных многогранников, приведены на рис. 4.
Прямые симметрии остальных правильных многогранников можно описать не по отдельности, а все вместе. Условимся понимать под <p, q> любой правильный многогранник, кроме <3, 3>. Прямая, проходящая через центр <p, q> и любую вершину, проходит через противоположную вершину, и любой поворот на целое кратное 360/q градусов вокруг этой прямой является симметрией. Следовательно, для каждой такой прямой существуют, включая тождественное преобразование, (q – 1) различных симметрий. Каждая такая прямая соединяет две из N0 вершин; следовательно, всего таких прямых – N0/2, что дает (q – 1) > N0/2 симметрий. Кроме того, прямая, проходящая через центр многогранника <p, q> и центр любой грани, проходит через центр противоположной грани, и любой поворот вокруг такой прямой на целое кратное 360/р градусов является симметрией. Так как общее число таких линий равно N2/2, где N2 – число граней многогранника <p, q>, мы получаем (p – 1) N2/2 различных симметрий, включая тождественное преобразование. Наконец, прямая, проходящая через центр и середину любого ребра многогранника <p, q>, проходит через середину противоположного ребра, и симметрией является полуоборот вокруг этой прямой. Поскольку имеется N1/2 таких прямых, где N1 – число ребер многогранника <p, q>, мы получаем еще N1/2 симметрий. С учетом тождественного преобразования получаем
прямых симметрий. Других прямых симметрий нет, и имеется столько же обратных симметрий.
Хотя формула (3) была получена не для многогранника <3, 3>, нетрудно проверить, что она верна и для него. Таким образом, многогранник <3, 3>обладает 12 прямыми симметриями, многогранники <4, 3>и <3, 4>имеют по 24 симметрии, а многогранники <5, 3>и <3, 5>– по 60 симметрий.
Читатели, знакомые с абстрактной алгеброй, поймут, что симметрии многогранника <p, q> образуют группу относительно определенного выше «умножения». В этой группе прямые симметрии образуют подгруппу индекса 2, а обратные симметрии группу не образуют, так как нарушают свойство замкнутости и не содержат тождественного преобразования (единичного элемента группы). Обычно о группе прямых симметрий говорят как о группе многогранника, а полную группу симметрий называют его расширенной группой. Из рассмотренных выше свойств двойственных многогранников ясно, что любой правильный многогранник и двойственный ему многогранник имеют одну и ту же группу. Группа тетраэдра называется тетраэдрической группой, группа куба и октаэдра называется октаэдрической группой, а группа додекаэдра и икосаэдра – икосаэдрической группой. Они изоморфны знакопеременной группе А4 из четырех символов, симметрической группе S4 из четырех символов и знакопеременной группе А5 из пяти символов соответственно (см. также АЛГЕБРА АБСТРАКТНАЯ).
ФОРМУЛА ЭЙЛЕРА
Рассматривая таблицу, можно заметить интересное соотношение между числом вершин N0, числом ребер N1 и числом граней N2 любого выпуклого правильного многогранника <p, q>. Речь идет о соотношении
которое называется формулой Эйлера в честь открывшего ее Л.Эйлера (1707–1783). Левая часть формулы (4) называется «эйлеровой характеристикой».
Формула Эйлера используется в сочетании с формулами (2) и (3). Из (4) и (2) получаем:
Отсюда следует выражение для N1 через p и q:
Воспользовавшись еще раз формулой (2), находим аналогичные выражения для N0 и N2:
Подставляя полученные выражения в формулы (3) и (4), получаем, что число прямых симметрий многогранника <p, q> равно
Это число можно записать также в одной из эквивалентных форм: qN0, 2N1 или pN2.
Область применения формулы Эйлера.
Значимость формулы Эйлера усиливается тем, что она применима не только к платоновым телам, но и к любому многограннику, гомеоморфному сфере (см. ТОПОЛОГИЯ). Это утверждение доказывается следующим образом.
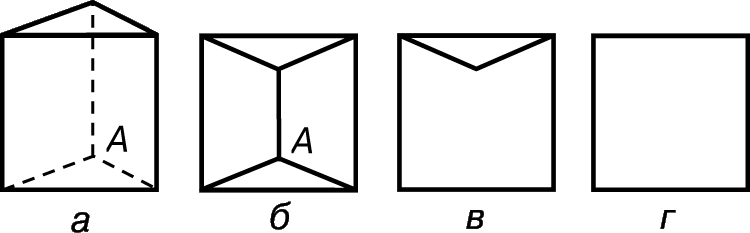
Пусть P – любой многогранник, гомеоморфный сфере, с N0 вершинами, N1 ребрами и N2 гранями; пусть c = N0 – N1 + N2 – эйлерова характеристика многогранника P. Требуется доказать, что c = 2. Так как Р гомеоморфен сфере, мы можем удалить одну грань и превратить остальные в некоторую конфигурацию на плоскости (например, на рис. 5,а и 5,б вы видите призму, у которой удалена передняя плоскость). «Плоскостная конфигурация» представляет собой сеть точек и прямолинейных отрезков, называемых соответственно «вершинами» и «ребрами», при этом вершины служат концами ребер. Вершины и ребра рассматриваемой нами конфигурации мы считаем смещенными и деформированными вершинами и ребрами многогранника. Таким образом, эта конфигурация имеет N0 вершин и N1 ребер. Остальные N2 – 1 граней многогранника деформируются в N2 – 1 непересекающихся областей на плоскости, определяемой конфигурацией. Назовем эти области «гранями» конфигурации. Вершины, ребра и грани конфигурации и определяют эйлерову характеристику, которая в данном случае равна c – 1.
Теперь мы проведем сплющивание так, что если удаленная грань была р-угольником, то все N2 – 1 граней конфигурации заполнят внутренность р-угольника. Пусть А – некоторая вершина внутри р-угольника. Предположим, что в А сходятся r ребер. Если удалить А и все r сходящихся в ней ребер, то число вершин уменьшится на 1, ребер – на r, граней – на r – 1 (см. рис. 5,б и 5,в). У новой конфигурации N ў 0 = N0 – 1 вершин, N ў 1 = N1 – r ребер и N ў 2 = N2 – 1 – (r – 1) граней; следовательно,
Таким образом, удаление одной внутренней вершины и сходящихся в ней ребер не меняет эйлеровой характеристики конфигурации. Поэтому, удалив все внутренние вершины и сходящиеся в них ребра, мы тем самым сведем конфигурацию к р-угольнику и его внутренности (рис. 5,г). Но эйлерова характеристика останется по-прежнему равной c – 1, а так как конфигурация имеет р вершин, р ребер и 1 грань, мы получаем
Таким образом, c = 2, что и требовалось доказать.
Далее можно доказать, что если эйлерова характеристика многогранника равна 2, то многогранник гомеоморфен сфере. Иначе говоря, мы можем обобщить полученный выше результат, показав, что многогранник гомеоморфен сфере в том и только в том случае, если его эйлерова характеристика равна 2.
Обобщенная формула Эйлера.
Для классификации других многогранников используется обобщенная формула Эйлера. Если у некоторого многогранника 16 вершин, 32 ребра и 16 граней, то его эйлерова характеристика равна 16 – 32 + 16 = 0. Это позволяет утверждать, что данный многогранник принадлежит классу многогранников, гомеоморфных тору. Отличительной особенностью этого класса является эйлерова характеристика, равная нулю. Более общо, пусть Р – многогранник с N0 вершинами, N1 ребрами и N2 гранями. Говорят, что данный многогранник гомеоморфен поверхности рода n в том и только в том случае, если
Наконец, следует заметить, что ситуация существенно усложняется, если смягчить прежнее ограничение, согласно которому никакие две грани многогранника не должны пересекаться. Например, появляется возможность существования двух негомеоморфных многогранников с одной и той же эйлеровой характеристикой. Их следует различать по другим топологическим свойствам.