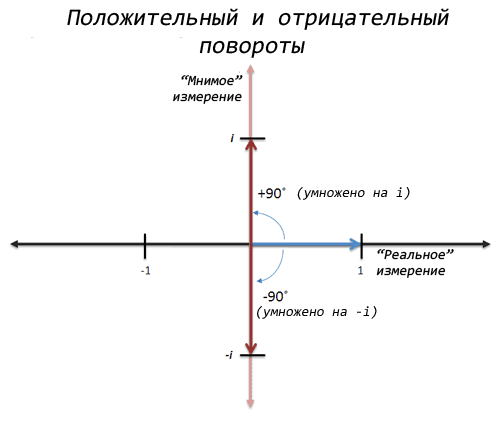
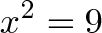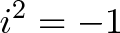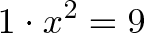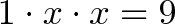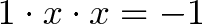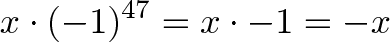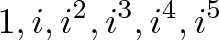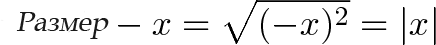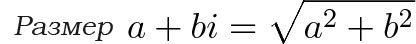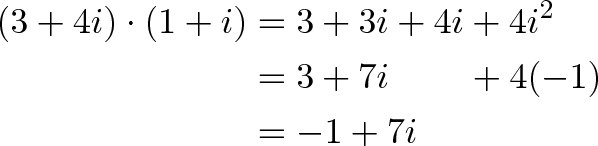что такое мнимая единица в математике

Мнимая единица – число на грани мистики

Человеку не сведущим в математике и физике рассуждения о мнимой единице представляется полным бредом. Например, квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Отсюда ясно, что квадратные корни из отрицательных чисел не могут находиться среди возможных действительных чисел. Следовательно, нам не остается ничего другого, как признать их невозможными числами.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел. Это было сделано китайскими математиками во II веке до н. э. Отрицательные числа не так просты. Представьте, сколько будет 3 – 4? Как можно отнять 4 барана от 3? Отрицательные числа рассматривались как полная чушь. Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число Е и много еще чего, не понимал отрицательные числа так же хорошо, как

мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений. Древнегреческие математики считали «настоящими» только натуральные числа.

То, что называют мнимым числом, на самом деле частный случай комплексного числа. Это число настоящим числом назвать нельзя. Учебники описывают его как величину, которая, будучи возведенной в квадрат, дает минус один. Другими словами, это сторона квадрата с отрицательной площадью. В реальности такого не бывает. Впервые понятие «мнимая величина» использовал Кардано (1545). Он решал задачу с помощью квадратных уравнений

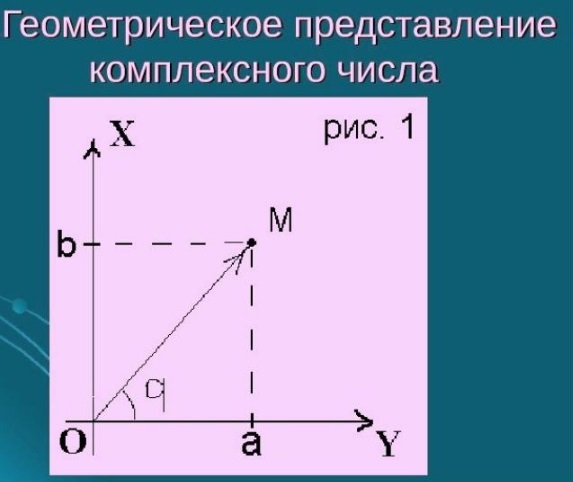
Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс означает связь, сочетание, совокупность понятий, предметов, явлений образующих единое целое. В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изобразить комплексное число z = a + b × i точкой m (a, b) на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M, а вектором, идущим в эту точку из начала координат. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. В дальнейшем Леонард Эйлер (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) получил знаменитую формулу, и открыл комплексным числам дорогу в самые различные области математики и ее приложений.

Комплексные числа – расширили понятие числа. В 1843 году ирландский математик Уильям Гамильтон предложил четырехмерную систему комплексных чисел, которая стала первой гиперкомплексной системой, названную кватернионами. Теория кватернионов вскоре стала одним из источников дальнейшего развития математики и ее приложений.

Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения.

Источник

Откуда есть пошло комплексное число

В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.

Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.

Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде:
.
Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой и параболы
Я тут даже картинку сделал, для иллюстрации.

Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:

Оказываются возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.

В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).

Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.

Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду: . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
Взгляните на картинку:

Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. Т.е., уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение.
Найти его можно воспользовавшись формулой Кардано:

где
.
Немного громоздко, но пока, вроде бы, все в порядке. Или нет?

Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.

Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс.
Возьмем классический пример, который рассматривал еще Бомбелли:
.
Внезапно,
,
и, соответственно,
.
Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.

Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.

Используя подобный подход, Бомбелли установил, в частности, что
,
и
.
Давайте проверим:
.
Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.

В сумме получаем . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.

Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.

Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) знаменитой формулы

открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.

Источник

Мнимая единица

Маяковский про мнимую единицу

Мнимая единица (讠, один с точечкой) — это:

Эта вторая формулировка крайне сложна. Чтобы её понять и привести к простой, нужно разбить одно окно чем-нибудь, другое — головой. И сравнить осколки обоих стёкол и состояние головы и крыши до и после процедуры.

Содержание

История открытия [ править ]

Основные свойства [ править ]

После того, как сбрендившие учёные поняли, что такое мнимая единица, стали выводить разные формулы. Например:

2 i = 2 i e e = 21 ⋅ e e = 21 <\displaystyle 2i=<\frac <2ie>>=<\frac <21\cdot e>>=21>

Тождество Эйлера [ править ]

Существует следующее тождество:

Его высказал Эйлер, один из трезвых учёных, во сне. Поэтому его называют тождеством Эйлера. До сих пор учёные всего мира не понимают смысл этой формулы и удивляются её странностью. Не меньше удивления вызывает то, что этот великий математик подарил открытие миру в спящем состоянии. Он, проснувшись, показывал, что ничего не помнит, что ему «опять снились эти формулы бессмысленные». Но никто и не подумал пренебрегать великим открытием. Все без исключения должны верить тому, что сказал Эйлер, поскольку он уже сделал много великих открытий. Он просто не захотел раскрывать строгого доказательства. Известны несколько доказательств, но известны и их опровержения.

Доказательство [ править ]

e − i π ∗ e i π = ( − 1 ) ∗ ( − 1 ) <\displaystyle e^<-i\pi >*e^=(-1)*(-1)>

В итоге мы получили верное равенство, которое вытекает из исходного, поэтому тождество Эйлера доказано!

Опровержение [ править ]

e i π + 1 = e 1 ⋅ π + 1 = e π + 1 ≠ 0 <\displaystyle e^+1=e^<1\cdot \pi >+1=e^<\pi >+1\neq 0>

Опровержение опровержения [ править ]

Не верьте этому опровержению, Эйлер говорил правду. (остальные 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 472 восклицательных знака были удалены автоматическим фильтром)

Следствие 1 [ править ]

Из тождества Эйлера следует нечто совсем уж парадоксальное. Перепишем тождество Эйлера в таком виде:

Поскольку в правой части равенства стоит действительное число, значит и в левой части тоже действительное число. В таком случае мы можем смело возвести обе части этого равенства в квадрат:

Следствие 2 [ править ]

Еще раз рассмотрим вышеприведённое тождество Эйлера:

А теперь возведем обе его части в любую целую нечётную степень n:

А значит, при любом нечётном n,

Интересные факты [ править ]

Человекам далеко не сведущим в математике, физике и алгебре, да что уж там — геометрии, рассуждения о мнимой единице представляется полным бредом. Прежде чем о ней рассуждать необходимо определиться, что такое отрицательные числа в природе. Дак, вот их НЕТ. Также как не может быть отрицательной скорости. Отрицательные числа прибывают в нашем воображении из-за того, что мы принимаем какое-либо значение за НОЛЬ. К примеру рассмотрим температуру вещества, а именно абсолютный ноль по Цельсию, это −273,15 °C (-459,67° по Фаренгейту), то есть полный покой вещества, когда его атомы «обездвижены» — вот это и есть НОЛЬ. Отсюда следует отрицательные числа, которые кажутся таковыми, следует записывать в скобках, например так:(-1). Физический смысл отрицательной степени — отсутствует. i 2 = − 1 <\displaystyle i^<2>=-1> далее

В итоге Эйлером доказано, что 1=-1, такой же единице только по другую сторону шкалы.

Источник

Мнимые числа для описания реальности?

Новый мысленный эксперимент показывает, что квантовая механика не работает без странных чисел, которые становятся отрицательными при возведении в квадрат.

Много веков назад математики были обеспокоены, когда обнаружили, что вычисление свойств определенных кривых требует, казалось бы, невозможного: чисел, которые при умножении сами на себя становятся отрицательными.

Однако физики, возможно, только что впервые показали, что мнимые числа в определенном смысле вещественны.

Группа теоретиков в области квантовой физики разработала эксперимент, результат которого зависит от того, есть ли у природы мнимая сторона. При условии, что квантовая механика верна — предположение, с которым мало кто поспорит, — аргумент команды по существу гарантирует, что комплексные числа являются неизбежной частью описания материальной вселенной.

«Эти комплексные числа обычно являются просто удобным инструментом, но здесь оказывается, что они действительно имеют какое-то материальное значение», — сказал Тамаш Вертези, физик из Института ядерных исследований Венгерской академии наук, который много лет назад утверждал обратное. «Мир таков, что ему действительно нужны эти комплексные числа», — сказал он.

В квантовой механике поведение частицы или группы частиц выражается волнообразным объектом, известным как волновая функция или ψ. Волновая функция прогнозирует вероятные результаты измерений, такие как вероятное положение или импульс электрона. Так называемое уравнение Шрёдингера описывает, как волновая функция изменяется во времени — и это уравнение включает i.

Физики никогда не знали, что с этим делать. Когда Эрвин Шрёдингер вывел уравнение, которое теперь носит его имя, он надеялся избавиться от i. «Что неприятно и против чего прямо следует возражать, так это против использования комплексных чисел, — писал он Хендрику Лоренцу в 1926 году, — Ψ, безусловно, является вещественной функцией».

Желание Шрёдингера, безусловно, было правдоподобным с математической точки зрения: любое свойство комплексных чисел может быть зафиксировано комбинациями вещественных чисел, а также новыми правилами, открывая математические возможности полностью вещественной версии квантовой механики.

Действительно, переход оказался достаточно простым, так что Шрёдингер почти сразу открыл то, что он считал «истинным волновым уравнением», которое «сторонилось» i. «Еще один камень с души упал», — написал он Максу Планку менее чем через неделю после своего письма Лоренцу. Все вышло именно так, как хотелось.

Но использование вещественных чисел для моделирования сложной квантовой механики неудобное и абстрактное занятие, и Шрёдингер признал, что его полностью вещественное уравнение слишком громоздко для повседневного использования. В течение года он описывал волновые функции как комплексные, в том виде, в каком их представляют сегодня физики.

«Любой, кто хочет выполнить работу, использует комплексное описание», — сказал Мэтью МакКейг, учёный в области информатики из Технологического университета Квинсленда в Австралии.

Однако формулировка квантовой механики с помощью вещественных чисел сохранилась как свидетельство того, что комплексная версия просто необязательна. Например, команды, включая Вертези и МакКейга, показали в 2008 и 2009 годах, что и без i они могут идеально предсказать результат известного эксперимента в квантовой физике, известного как тест Белла.

Новое исследование, которое было опубликовано на сервере научных препринтов arxiv.org в январе, обнаружило, что ранние предложения по тестам Белла просто недостаточно продвинулись, чтобы опровергнуть версию квантовой физики с вещественными числами. Это исследование предлагает более сложный эксперимент Белла, который, похоже, требует комплексных чисел.

Ранние исследования привели людей к выводу, что «в квантовой теории комплексные числа лишь удобны, но не необходимы», — писали авторы, в число которых входят Марк-Оливье Рену из Института фотонных наук в Испании и Николя Жизен из Женевского университета. «Мы доказываем ошибочность этого вывода».

Группа отказалась публично обсуждать свою работу, поскольку он все еще находится на экспертной оценке.

Тест Белла показывает, что пары удаленных друг от друга частиц могут обмениваться информацией в едином «запутанном» состоянии. Если бы монета 25 центов в штате Мэн могла «запутаться», например, с такой же монетой в Орегоне, то повторяющиеся подбрасывания показали бы, что всякий раз, когда одна монета падает орлом, ее дальний партнер, как ни странно, выпадет решкой. Точно так же в стандартном эксперименте теста Белла запутанные частицы отправляются двум физикам с вымышленными именами Алиса и Боб. Они измеряют частицы и, сравнивая измерения, обнаруживают, что результаты коррелированы таким образом, что это не поддаётся объяснению, разве что частицы обмениваются информацией.

Модернизированный эксперимент добавляет второй источник пар частиц. Одна пара достается Алисе и Бобу. Вторая пара, «родом» из другого места, отправляется Бобу и третьему лицу, Чарли. В квантовой механике с комплексными числами частицы, которые получают Алиса и Чарли, не обязательно должны быть запутаны друг с другом.

Однако никакое описание в виде вещественных чисел не может воспроизвести модель корреляций, которую будут измерять три физика. В новой статье показано, что рассмотрение системы как вещественной требует введения дополнительной информации, которая обычно находится в мнимой части волновой функции. Частицы Алисы, Боба и Чарли должны разделять эту информацию, чтобы воспроизводить те же корреляции, что и в стандартной квантовой механике. И единственный путь приспособиться к этому разделению — это перепутать все их частицы друг с другом.

В предыдущих воплощениях теста Белла электроны Алисы и Боба поступали из одного источника, поэтому дополнительная информация, которую они должны были нести в описании вещественных чисел, не представляла проблемы. Но в тесте Белла с двумя источниками, где частицы Алисы и Чарли происходят из независимых источников, фиктивная трехсторонняя запутанность не имеет физического смысла.

Даже без привлечения Алисы, Боба и Чарли для фактического проведения эксперимента, который представляет новая статья, большинство исследователей крайне уверены, что стандартная квантовая механика верна и, следовательно, эксперимент найдет ожидаемые корреляции. Если это так, то одни только вещественные числа не могут полностью описать природу.

«В статье устанавливается, что существуют истинные комплексные квантовые системы», — сказал Вальтер Моретти, физик-математик из Университета Тренто в Италии. Этот результат стал для него совершенно неожиданным.

Тем не менее велика вероятность того, что когда-нибудь эксперимент состоится. Это будет непросто, но технических препятствий нет. И глубокое понимание поведения усложняющихся квантовых сетей будет становиться все более актуальным, поскольку исследователи продолжают связывать многочисленные Алисы, Бобы и Чарли через возникающие квантовые сети.

«Поэтому мы верим, что опровержение вещественной квантовой физики произойдет в ближайшем будущем», — пишут авторы.

Источник

Просто о сложном: комплексные числа

Комплексные числа всегда меня занимали. Как и с понятием экспоненты, большинство определений подпадали под одну из двух категорий:

Какой хороший способ привлечь деток к математике! Сегодня мы возьмем эту тему штурмом, используя наши любимые инструменты:

И наше секретное оружие: изучение по аналогии. Мы доберемся до комплексных чисел, начав с их предков, отрицательных чисел. Вот вам небольшое руководство:

Пока что смысла в этой таблице мало, но пусть она будет рядом. К концу статьи всё станет на свои места.

Давайте действительно поймем, что такое отрицательные числа

Отрицательные числа не так просты. Представьте, что вы — европейский математик в XVIII веке. У вас есть 3 и 4, и вы можете написать 4 – 3 = 1. Всё просто.

Но сколько будет 3 – 4? Что, собственно, это означает? Как можно отнять 4 коровы от 3? Как можно иметь меньше, чем ничего?

Отрицательные числа рассматривались как полная чушь, что-то, что «бросало тень на всю теорию уравнений» (Фрэнсис Масерес, 1759). Сегодня было бы полной чушью думать об отрицательных числах, как о чем-то нелогичном и неполезном. Спросите вашего учителя, нарушают ли отрицательные числа основы математики.

Что же произошло? Мы изобрели теоретическое число, которое обладало полезными свойствами. Отрицательные числа нельзя потрогать или ощутить, но они хорошо описывают определенные связи (как задолженность, например). Это очень полезная выдумка.

Вместо того, чтобы сказать «Я должен вам 30», и читать слова, чтобы понять в плюсе я или в минусе, я могу просто записать «-30», и знать, что это означает. Если я заработаю деньги и оплачу свои долги (-30 + 100 = 70), я смогу легко записать эту транзакцию несколькими символами. У меня останется +70.

Знаки плюса и минуса автоматически фиксируют направление — вам не нужно целое предложение, чтобы описать изменения после каждой транзакции. Математика стала проще, элегантнее. Стало не важно, являются ли отрицательные числа «осязаемыми» — у них есть полезные свойства, и мы пользовались ими, пока они крепко не вошли в наш обиход. Если кто-то из ваших знакомых еще не понял суть отрицательных чисел, теперь вы ему поможете.

Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число е и много еще чего, не понимал отрицательные числа так же хорошо, как мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений.

Странно требовать от детей, чтобы они спокойно понимали идеи, которые когда-то смущали даже самых лучших математиков.

Ввод мнимых чисел

С мнимыми числами та же история. Мы можем решать уравнения вроде этого целыми днями:

Ну и ну. Такой вопрос заставляет людей съеживаться, первый раз видя его. Вы хотите вычислить квадратный корень из числа, меньшего, чем ноль? Это немыслимо! (Исторически реально существовали подобные вопросы, но мне удобнее представлять какого-то безликого умника, чтобы не вгонять в краску ученых прошлого).

Выглядит безумно, как в свое время выглядели и отрицательные числа, ноль и иррациональные числа (неповторяющиеся числа). В этом вопросе нет «реального» смысла, правда?

Ну, сначала у нас конечно болит голова. Но, играя в игру «Давайте представим, что i существует», мы действительно делаем математику проще и элегантнее. Появляются новые связи, которые мы с легкостью можем описать.

Я не люблю сам термин «мнимые числа» — такое чувство, что он был выбран специально, чтобы оскорбить чувства i. Число i такое же нормальное, как и другие, но за ним закрепилась кличка «мнимое», так что мы тоже будем ей пользоваться.

Визуальное понимание отрицательных и комплексных чисел

Уравнение x^2 = 9 на самом деле означает следующее:

Какое преобразование x, применяемое дважды, превращает 1 в 9?

Это довольно круто! У нас есть что-то вроде решения, но что оно означает?

Все числа 2-мерные. Да, это трудно принять, но древним римлянам было бы также трудно принять десятичные дроби или деление в столбик. (Как это так, между 1 и 2 есть еще числа?). Выглядит странно, как и любой новый способ мыслить в математике.

Также, не забывайте, что принятие оборота против часовой стрелки за положительный результат — это сугубо человеческая условность, и всё могло бы быть совсем по-другому.

Поиск множеств

Это очень полезная мысль. Число «х» может представлять хорошие и плохие недели. Представим, что хорошая неделя сменяет плохую; это хорошая неделя; а какой будет 47-я неделя?

-x означает, что неделя выдастся плохой. Видите, как отрицательные числа «следят за знаком» — мы можем просто ввести (-1)^47 в калькуляторе вместо того, чтобы считать («Неделя 1 хорошая, неделя 2 плохая… неделя 3 хорошая…»). Вещи, которые постоянно чередуются можно отлично смоделировать, используя отрицательные числа.

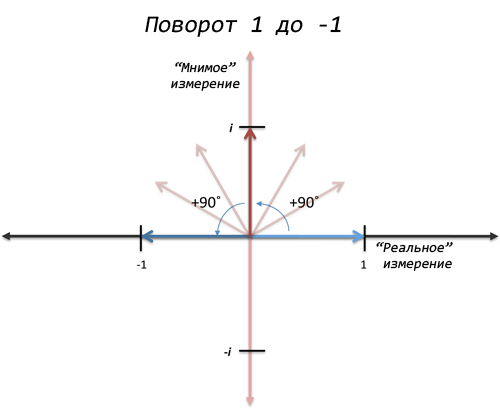
Хорошо, а что будет, если мы продолжим умножать на i?

Очень смешно, давайте немного это всё упростим:

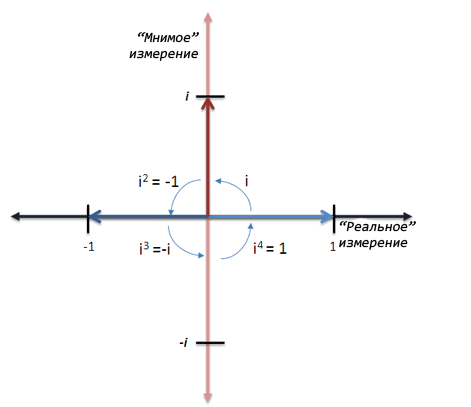
Вот всё то же представлено графически:

Мы повторяем цикл каждый 4-й поворот. В этом определенно есть смысл, да? Любой ребенок скажет вам, что 4 поворота влево — это всё равно, что не поворачиваться вовсе. А теперь оторвитесь от мнимых чисел (i, i^2)и посмотрите на общее множество:

Точно, как отрицательные числа моделируют зеркальное отражение чисел, мнимые числа могут моделировать что угодно, что вращается между двумя измерениями «Х» и «Y». Или что угодно с циклической, круговой зависимостью — есть что-нибудь на примете?

Понимание комплексных чисел

Есть еще одна деталь для рассмотрения: может ли число быть и «реальным», и «мнимым»?

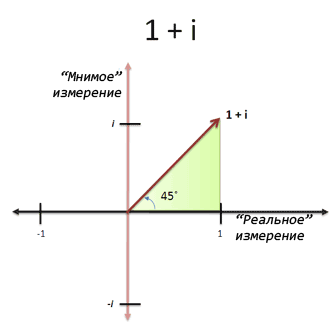
Даже не сомневайтесь. Кто сказал, что нам обязательно нужно поворачивать строго на 90 градусов? Если мы одной ногой станем на «реальную» размерность, а другой — на «мнимую», то будет выглядеть примерно так:

Мы находимся на отметке в 45 градусов, где вещественная и мнимая части одинаковы, и само число равно «1 + i». Это как хот-дог, где есть и кетчуп, и горчица — кто сказал, что нужно обязательно выбирать что-то одно?

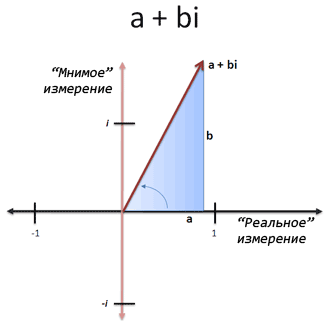
По сути, мы можем выбрать любую комбинацию вещественной и мнимой части и сделать из всего этого треугольник. Угол становится «углом вращения». Комплексное число — это заумное название для чисел, в которых есть вещественная и мнимая части. Они пишутся, как «a + bi», где:

Неплохо. Но остается один последний вопрос: как «велико» комплексное число? Мы не можем измерить вещественную часть или мнимую отдельно, потому что мы упустим общую картину.

Давайте сделаем шаг назад. Размер отрицательного числа — это расстояние от нуля:

Это другой способ найти абсолютную величину. Но как измерить оба компонента на 90 градусах для комплексных чисел?

Это птица в небе… или самолет… Пифагор спешит на помощь!

Эта теорема выскакивает, где только можно, даже в числах, придуманных через 2000 лет после самой теоремы. Да, мы делаем треугольник, и его гипотенуза и будет равна расстоянию от нуля:

Реальный пример: Вращения

Мы не будем дожидаться университетского курса физики, чтобы попрактиковаться с комплексными числами. Мы займемся этим уже сегодня. Много можно рассказать на тему умножения комплексных чисел, но пока нужно понять главное:

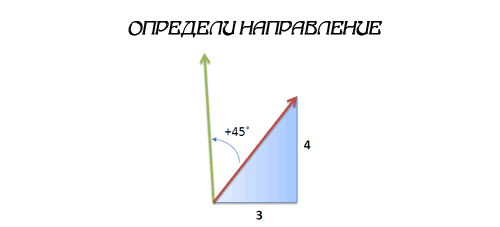
Давайте посмотрим, как это работает. Представьте, что я на лодке, движусь с курсом 3 единицы на Восток каждые 4 единицы на Север. Я хочу изменить свой курс на 45 градусов против часовой стрелки. Каким будет мой новый курс?

Кто-то может сказать «Это просто! Вычислите синус, косинус, погуглите значение по тангенсу…и тогда…» Кажется, я сломал свой калькулятор…

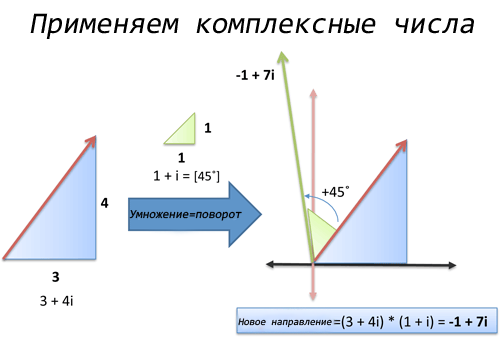
Давайте пойдем более простым путем: мы идем по курсу 3 + 4i (не важно, какой тут угол, нам всё равно пока) и хотим повернуться на 45 градусов. Ну, 45 градусов это 1 + i (идеальная диагональ). Так что мы можем умножить наш курс на это число!

При умножении мы получаем:

Наш новый ориентир — 1 единица на Запад (-1 на Восток) и 7 единиц на Север, можете нарисовать координаты на графике и следовать им.

Но! Мы нашли ответ за 10 секунд, без всяких синусов и косинусов. Не было векторов, матриц, отслеживания, в каком квадранте мы находимся. Это была простая арифметика и немного алгебры для приведения уравнения. Мнимые числа отлично справляются с вращением!

Более того, результат такого вычисления очень полезен. У нас есть курс (-1, 7) вместо угла (atan(7/-1) = 98.13, и сразу ясно, что мы во втором квадранте. Как, собственно, вы планировали нарисовать и следовать указанному углу? Используя транспортир под рукой?

Нет, вы бы конвертировали угол в косинус и синус (-0.14 и 0.99), нашли бы примерное соотношение между ними (около 1 к 7) и набросали бы треугольник. И тут комплексные числа несомненно выигрывают — аккуратно, молниеносно, и без калькулятора!

Если вы похожи на меня, то это открытие покажется вам сногсшибательным. Если нет, боюсь, что математика вас совсем не зажигает. Уж извините!

Тригонометрия хороша, но комплексные числа значительно упрощают вычисления (вроде поиска cos(a + b)). Это только маленький анонс; в следующих статьях я предоставлю вам полное меню.

Лирическое отступление: некоторые люди думают примерно так: «Эй, ну не удобно же иметь курс Север/Восток вместо простого угла для следования судна!»

Правда? Ну хорошо, посмотрите на свою правую руку. Какой угол между основанием вашего мизинца и кончиком указательного пальца? Удачи с вашим способом вычисления.

А можно просто ответить «Ну, кончик находится на Х дюймов вправо и Y дюймов вверх» и с этим уже можно что-то сделать.

Комплексные числа стали ближе?

Мы пронеслись смерчем по моим базовым открытиям в области комплексных чисел. Посмотрите на самую первую иллюстрацию, теперь он должен стать более понятным.

Есть еще столько всего интересного в этих красивых, чудных числах, но мой мозг уже устал. Моя цель была проста:

Если я кажусь слишком озабоченным этой темой, то для этого есть причина. Мнимые числа годами были моей навязчивой идеей — недостаток понимания меня раздражал.

Сейчас я наконец-то дошел до этого долгожданного понимания, и мне не терпелось поделиться с вами. Но меня по-прежнему злит, что вы знакомитесь с этими замечательными, несложными приемами понимания в блоге какого-то безумного лунатика, а не в классе на уроке математики. Мы душим в себе вопросы и «пыхтим» над непонятными вещами, потому что не хотим искать, находить и делиться чистыми, абсолютно логичными объяснениями.

Но зажечь свечу лучше, чем пробираться сквозь кромешную тьму: вот мои мысли, и я уверен, что огонек зажжется и в умах моих читателей.

Эпилог: Но они по-прежнему довольно странные!

Я знаю, они и для меня всё еще выглядят странными. Я пытаюсь мыслить, как мыслил первый человек, открывший ноль.

Ноль — это такая странная идея, «что-то» представляет «ничего», и это никак не могли понять в Древнем Риме. То же самое и с комплексными числами — это новый способ мышления. Но и ноль, и комплексные числа значительно упрощают математику. Если бы мы никогда не внедряли странности вроде новых систем счисления, мы бы до сих пор считали всё на пальцах.

Я повторяю эту аналогию, потому что так легко начать думать, что комплексные числа «не нормальные». Давайте быть открытыми к новшествам: в будущем люди будут только шутить над тем, как кто-то вплоть до XXI века не верил в комплексные числа.

Источник