что такое минуты в таблице брадиса

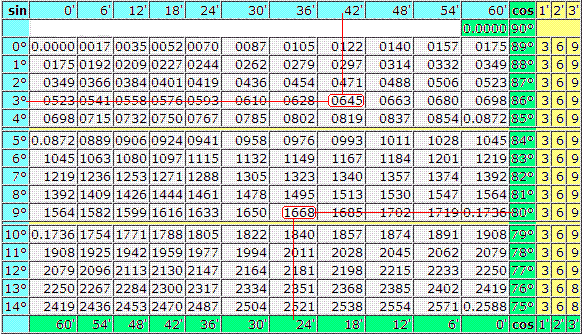
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.

sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.

Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.

Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:

sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо

sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654

Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.

cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо

Таблица Брадиса.

Таблица разбита на 2 части. В 1-ой части таблицы Брадиса тангенсы от 0° до 75° и котангенсы от 15° до 90° определяются с помощью дополнительных столбиков для 1’, 2’ и 3’ (минуты). Во 2-ой части тангенсы от 75° до 90° и котангенсы от 0° до 15° записаны в таблице с точностью до 1’ угла.

Источник

eponim2008

Жизнь замечательных имен

Короткие истории о вещах и о людях, давших им свое имя

Как пользоваться таблицей Брадиса?

Советские инженеры постепенно становятся легендой. Многим нынешним обладателям инженерного диплома кажется невероятным, что эти ребята за нищенскую, в общем, зарплату строили гигантские заводы, прокладывали железные дороги и конструировали самолеты и ракеты, которые взлетали и летали, а также корабли, которые бороздили. И делали они это едва ли не с пустыми руками. Что было инструментом советского инженера? Кульман, ватман, карандаш, логарифмическая линейка да таблицы Брадиса.

Математик Владимир Модестович Брадис (1890 – 1975) еще в начале 20-го века придумал способ, позволяющий до минимума сократить утомительные расчеты, которые приходилось производить каждому инженеру до появления калькуляторов. Он выбрал несколько наиболее необходимых для практических расчетов функций и посчитал все их значения в широком интервале аргументов с приемлемой точностью, четыре значащих цифры. Результаты своих расчетов В.М.Брадис представил в виде таблиц. Функции, отобранные В.М.Брадисом для расчетов, были следующие: квадраты и кубы, квадратные и кубические корни, обратная функция 1/x, тригонометрические функции (синусы, косинусы, тангенсы), экспонента и логарифмы Для каждой функции была рассчитана своя таблица. Все таблицы были напечатаны в виде небольшой брошюры. Эта брошюра в советское время переиздавалась едва ли не ежегодно и была очень востребована.

Таблицы Брадиса имеют одинаковую для всех функций структуру. Значения аргументов находятся в левом столбце и в верхней колонке. Соответствующее значение функции расположено в клетке, находящейся на пересечении столбца и колонки, которые задают значение аргумента.

Возьмем для примера таблицу синусов. Допустим, следует определить, чему равно значение синуса для угла 10 градусов и 30 минут. Находим в левом столбце значение 10 градусов (11-я строка), а в верхней колонке – 30 минут (6-й столбец). На пересечении 11 строки и 6-го столбца, находим значение функции, 0.1822. Три последних столбца предназначены для уточнения значений минут. Дело в том, что в верхней колонке значения представлены только значения минут, кратные 6. Для определения синуса для других значений аргумента следует прибавить или вычесть поправку из ближайшего значения функции, представленного в таблице. Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828.

Поскольку синус и косинус, тангенс и котангенс для данного угла взаимосвязаны, по таблице синусов можно определять и значения косинусов, а по таблице тангенсов – значения котангенсов. Но аргумент для косинуса и для котангенса следует искать в правом столбце (четвертом справа) и в нижней строке.

Аргументы тригонометрических функций в таблицах Брадиса заданы в градусах. Для перевода градусов в радианы значение угла следует умножить на 180 и разделить на 3.1415926. Кстати, таблицы радианной меры угла тоже были сосчитаны В.М.Брадисом и их можно отыскать в брошюре.

Как видим, таблицы В.М.Брадиса позволяют определять четыре значащих цифры любой функции. Поэтому они называются «четырехзначными». Такой точности расчетов заведомо хватает для 90% инженерных расчетов.

В настоящее время, когда калькуляторы есть и в часах, и в мобильных телефонах, расчеты функций по таблицам Брадиса можно считать «пережитком прошлого». Но, скажем честно, славного прошлого. Большое ведь видится на расстоянии. И ракеты тогда все-таки взлетали.

Источник

Математические таблицы Брадиса

Значения, приводимые в математических таблицах Брадиса – результат округления точных значений до второго, третьего или четвёртого знака после запятой. В приведённой таблице, используя «готовые поправки» из трёх колонок справа, можно, путём интерполяции, получить значение тангенса и котангенса для любого острого угла от 0° до 76°, заданного с точностью до минуты.

Пример:
tg 60° 15′ = 1,746 + 0,004 = 1,750 (прибавляется поправка на 3′, равная 0,004, которая берётся из соответствующей правой колонки).

Если избыток данного значения аргумента составляет 4′ или 5′ (т.е. больше половины ступени в 6′), то надо применять поправку на 2′ или на 1′, вычитая её из ближайшего большего значения функции. Это даёт выигрыш в точности, так как малые поправки точнее больших. Например:

Некоторые табличные значения подчёркнуты. Это означает, что целую часть для них надо брать не на этой, а на следующей строчке.

Числа с штрихами (‘), находящиеся в трёх правых колонках, а так же вверху и внизу таблицы – это минуты угловой величины, позволяющие точнее задавать её значение. Математические таблицы Брадиса являются универсальными, и могут применяться при решении задач (в дисциплинах: алгебра, тригонометрия, геометрия, физика) в старших классах общеобразовательной и специализированной школы, в колледжах, в гимназиях и, далее, в высших учебных заведениях, на практике, в работе.

Общие правила вычислений с помощью таблиц Брадиса:

Пример перевода числовых значений из десятых долей градусов в минуты:
10.8° (десять целых и восемь десятых градуса)
8 / 10 = X / 60
X = (8 * 60) / 10 = 48
Итог конвертации: 10.8° = 10° 48′ (десять градусов и сорок восемь минут).

Высокоточные вычисления тригонометрических функций для углов, заданных с точностью до минут и секунд – проводятся на специальных инженерных калькуляторах (в виде компьютерных программ, считающих до 32 разрядов или отдельного счётного прибора) и в электронных таблицах Excel по формуле, записанной в определённом формате. Пример строки с формулой в табличной ячейке для расчёта синуса угла, заданного с минутами и секундами:
E1 = sin (((A1 + B1/60 + C1/3600) * pi()) / 180)
где A1 – число градусов аргумента, заданное в первой строке колонки A.
B1 – минуты;
C1 – секунды.

При отсутствии таблиц Брадиса, инженерного калькулятора и компьютера, значения тригонометрических функций можно посчитать, с произвольно высокой точностью, и на простейшем арифмометре, с помощью аналитических операций сложения, вычитания, умножения и деления по формулам рядов:

В степень – число возводится с помощью многократного перемножения.
Например, аргумент в кубе: x^3 = x*x*x На калькуляторе, после набора числа, последовательно нажимаются кнопки: * = =

Если не нужна высокая точность и требуется быстрое вычисление, используются различные номограммы (нарисованные или напечатанные на бумаге и других материалах), логарифмические линейки и прочие приспособления и инструменты.

Таблицы Брадиса. Тангенсы и котангенсы

Смотреть, печатать трёхзначные таблицы: синус, косинус угла >>

Список использованной литературы и ссылки на Интернет-ресурсы

Таблицы Брадиса. Москва: Просвещение, 1968 г.

Источник