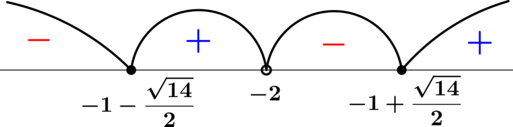что такое метод рационализации

Метод рационализации. Часть 2

Метод рационализации позволяет перейти от неравенства, содержащего сложные показательные, логарифмические и т.п. выражения, к равносильному ему более простому рациональному неравенству.

Хотите постичь суть метода рационализации, – придется разбираться с этим примером + показать

0,& &x-5>0; \end &\begin x+6

Также, мы могли бы, имея в руках совокупность

0,& &x-5>0; \end &\begin x+6

Мы вплотную подошли к методу рационализации в логарифмических неравенствах.

Метод рационализации в логарифмических неравенствах

Можно и видео посмотреть.

Здесь нет краткого решения неравенства методом рационализации, здесь подводка к методу, суть + показать

Рассмотрим неравенство .

Представляем 4 в виде логарифма:

.

Мы имеем дело с переменным основанием у логарифма, поэтому, в зависимости от того, больше 1 или меньше 1 основание логарифма (то есть с возрастающей или убывающей функцией мы имеем дело), знак неравенства сохранится или поменяется на «». Поэтому возникает совокупность (объединение) двух систем:

1,& &(x^2-4x)^2\leq(x-3)^4; \end &\begin x-3

Но, ВНИМАНИЕ, эта система должна решаться с учетом ОДЗ! Я специально не стала нагружать систему ОДЗ, чтобы не затерялась главная мысль.

Смотрите, вот мы сейчас перепишем нашу систему так (перенесем в каждой строке неравенства все в левую сторону):

0,& &(x^2-4x)^2-(x-3)^4\leq 0; \end &\begin x-3-1

Вам это ничто не напоминает? По аналогии с “Важно!” (см. выше) мы данную совокупность систем заменим неравенством:

.

Решив данное неравенство на ОДЗ мы и получим решение неравенства .

Найдем сначала ОДЗ исходного неравенства (ОДЗ для логарифмов смотрим здесь):

Решение последнего неравенства с учетом ОДЗ:

Ответ:

Метод рационализации в показательных неравенствах

Решим неравенство .

Решение исходного неравенства равносильно решению неравенства

.

Ответ: .

Метод рационализации в неравенствах, содержащих модуль

Работая с неравенствами типа , где функции от некоторой переменной, можем руководствоваться следующими равносильными переходами:

Решим неравенство

Перейдем к равносильному неравенству:

Ответ: .

Здесь предлагаю посмотреть краткую сводку-таблицу к теме “Рационализация неравенств”.

А здесь предлагаю еще рассмотреть несколько примеров по теме “Рационализация неравенств”.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Метод рационализации

\(\blacktriangleright\) Метод рационализации — это способ решения некоторых неравенств, который позволяет довольно сильно упростить решение и вычисления.

\(\blacktriangleright\) Рассмотрим метод рационализации для решения показательных неравенств вида \[<\Large<(h(x))^\geqslant (h(x))^>>\]

Если бы мы решали данное неравенство классическим способом, то оно было бы равносильно совокупности: \[ <\large<\left[\begin\begin &\begin h(x)>1\\ f(x)\geqslant g(x) \end\\[1ex] &\begin 0

По методу рационализации данное неравенство равносильно системе: \[ <\large< \begin(h(x)-1)(f(x)-g(x))\geqslant 0\\[1ex] h(x)>0 \end>>\]

Покажем, что решения совокупности и системы совпадают.

Первое неравенство системы равносильно \[(a)\quad \left[\begin \begin &\begin h(x)\geqslant1\\ f(x)\geqslant g(x) \end\\[1ex] &\begin h(x)\leqslant 1\\ f(x)\leqslant g(x) \end \end \end \right.\]

Совокупность равносильна \[(b)\quad \left[\begin \begin &\begin h(x)>1\\ f(x)\geqslant g(x)\\ h(x)=1 \end\\[1ex] &\begin 0

Заметим, что решение совокупности \((a)\) плюс условие \(h(x)>0\) и решение совокупности \((b)\) полностью совпадают.

\(\blacktriangleright\) Рассмотрим метод рационализации для решения логарифмических неравенств вида \[<\Large<\log_\geqslant \log_>>\]

Если бы мы решали данное неравенство классическим способом, то оно было бы равносильно совокупности: \[ <\large<\left[\begin\begin &\begin h(x)>1\\ f(x)\geqslant g(x)\\ g(x)>0 \end\\[1ex] &\begin 0 0 \end \end \end \right.>>\]

По методу рационализации данное неравенство равносильно системе: \[ <\large<\begin(h(x)-1)(f(x)-g(x))\geqslant 0\\[1ex] f(x)>0\\ g(x)>0\\ h(x)>0\\ h(x)\ne 1 \end>>\]

Покажем, что решения совокупности и системы совпадают.

Первое неравенство системы плюс условие \(h(x)\ne 1\) равносильно \[(c)\quad \left[\begin \begin &\begin h(x)>1\\ f(x)\geqslant g(x) \end\\[1ex] &\begin h(x)

Совокупность равносильна (если выписать часть ОДЗ отдельно) \[(d) \quad \begin f(x)>0\\ g(x)>0\\ h(x)>0\\[1ex] \left[\begin \begin &\begin h(x)>1\\ f(x)\geqslant g(x) \end\\ &\begin h(x)

Заметим, что решение совокупности \((c)\) плюс условия \(f(x)>0, g(x)>0, h(x)>0\) и решение совокупности \((d)\) полностью совпадают.

\(\blacktriangleright\) Если \(f(x), h(x), g(x)\) — многочлены (что бывает очень часто в задачах), то метод рационализации позволяет перейти от показательного или логарифмического неравенства к рациональному, которое уже легко решается методом интервалов.

Рассмотрим несколько примеров, показывающих удобство использования метода рационализации.

Пример 1. Решить неравенство \(\log_<(x^2-1)><\dfrac<2x^2+3x-5>>\leqslant 1\)

Выпишем и решим ОДЗ отдельно: \[\begin x^2-1>0\\ x^2-1\ne 1\\[1ex] \dfrac<2x^2+3x-5>>0 \end\Leftrightarrow \begin (x-1)(x+1)>0\\ x\ne \pm \sqrt 2\\[1ex] \dfrac<2(x-1)(x+2,5)>>0 \end\Leftrightarrow \begin x\in (-\infty;-1)\cup(1;+\infty)\\ x\ne \pm \sqrt 2\\ x\in (-2,5;-1)\cup(1;+\infty) \end \Leftrightarrow\]

\[\Leftrightarrow x\in (-2,5;-\sqrt 2)\cup(-\sqrt 2;-1)\cup(1;\sqrt 2)\cup(\sqrt 2;+\infty)\]

Полученное неравенство можно решить методом интервалов:

Таким образом, решением будут \(x\in (-\infty;-2]\cup[-\sqrt2;-1)\cup[1;\sqrt2]\cup[2;+\infty)\)

Пересечем данное решение с ОДЗ и получим \[x\in (-2,5;-2]\cup(-\sqrt2;-1)\cup(1;\sqrt2)\cup[2;+\infty)\]

\(\blacktriangleright\) Более общий случай применения метода рационализации:
если неравенство представлено в виде \(F(x)\lor 0\) ( \(\lor\) — один из знаков \(\geqslant, \leqslant, >, ), причем функция \(F(x)\) является произведением и/или частным нескольких множителей, то на ОДЗ:

Данное неравенство можно переписать в виде \((3+x-2x^2)(\log_<(3x+5)>-\log_1)\geqslant 0\) (т.к. \(\log_a1=0\) ).

Таким образом, неравенство представлено в необходимом нам виде: справа ноль, слева произведение двух скобок, причем одна из них — разность логарифмов с одинаковым основанием. Выпишем отдельно ОДЗ:

\(\begin x+2>0\\x+2\ne 1\\ 3x+5>0 \end \Leftrightarrow x\in \left(-\frac53;-1\right)\cup\big(-1;+\infty\big)\)

Тогда на ОДЗ можно заменить второй множитель по методу рационализации, т.е. исходное неравенство на ОДЗ равносильно неравенству:

\((3+x-2x^2)(x+2-1)(3x+5-1)\geqslant 0 \Leftrightarrow (2x^2-x-3)(x+1)(3x+4)\leqslant 0 \Leftrightarrow\)

\( \Leftrightarrow (2x-3)(x+1)(x+1)(3x+4)\leqslant 0 \Leftrightarrow x\in \left[-\frac43;\frac32\right]\)

Пересечем данное решение с ОДЗ и получим: \(x\in \left[-\frac43;-1\right)\cup\left(-1;\frac32\right]\)

Пример 3. Решить неравенство \((3^x-1)(0,25^x-16)(5x^2-9x-2)\leqslant0\)

Таким образом, неравенство равносильно:

\((3^x-3^0)(0,25^x-0,25^<-2>)(5x^2-9x-2)\leqslant 0 \Leftrightarrow\)

\(\Leftrightarrow (3-1)(x-0)(0,25-1)(x-(-2))(5x+1)(x-2)\leqslant0 \Leftrightarrow\)

Решив данное неравенство методом интервалов, получим \(x\in (-\infty;-2\big]\cup\left[-\frac15;0\right]\cup\big[2;+\infty)\)

Найдем ОДЗ данного неравенства:

Решим данное неравенство на ОДЗ.

Решим неравенство из совокупности методом интервалов:

Таким образом, решением данной совокупности будут

Пересекая данное решение с ОДЗ, получим итоговый ответ: \(x\in \<-1\>\cup[1;2)\)

Источник

Метод рационализации при решении неравенств в заданиях № 15 единого государственного экзамена

При решении неравенств в задании № 15 профильного уровня по математике рациональнее всего применять метод замены множителей. Этот метод не относится к стандартным школьным, но позволяет многие неравенства решать быстро и красиво.

С помощью условий равносильности сводят решения многих нераенств, содержащих показательные, логарифмические, иррациональные выражения и выражения с модулем, к решению рациональных неравенств классическим методом интервалов.

Содержимое разработки

метод рационализации при решении неравенств в заданиях № 15

Коротова Юлия Аликовна

у читель МАОУ СОШ № 13 имени П.А Леонова

Основные ошибки при решении неравенств (задание № 15)

Рациональный метод решения неравенств – метод равносильных преобразований по знаку (метод декомпозиции – Моденов В.П., метод замены множителей – Голубев В.И.)

Метод рационализации заключается

в замене сложного выражения F ( x ) на

области определения выражения F ( x ).

Алгоритм метода рационализации

то есть справа должен стоять 0, а все возможные слагаемые в левой

части необходимо привести к общему знаменателю (если среди

них встречаются дроби).

3. Явно указать ОДЗ исходного неравенства.

4. По возможности заменить все выражения u i и u k на более простые,

совпадающие по знаку с исходными.

5. Решить полученное неравенство.

6. Учитывая ОДЗ, записать ответ исходного неравенства.

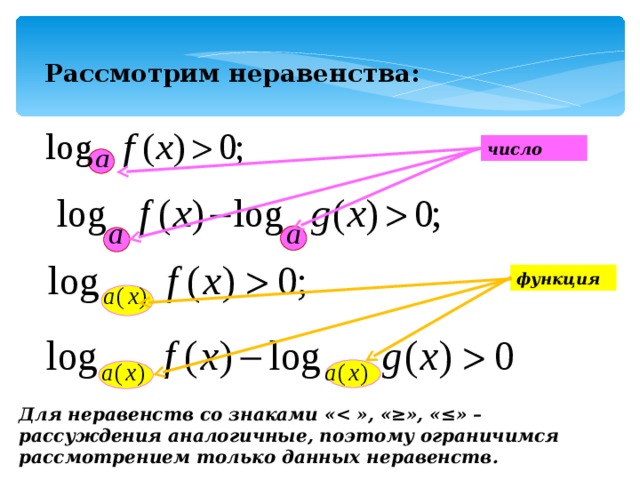
Для неравенств со знаками « », «≥», «≤» – рассуждения аналогичные, поэтому ограничимся рассмотрением только данных неравенств.

Теорема 1. Логарифмическое неравенство

равносильно следующей системе неравенств :

Источник

Неравенства, решаемые методом рационализации (страница 3)

\(\blacktriangleright\) Метод рационализации для логарифмической функции.
Так как у логарифмов уже появляются ограничения на ОДЗ, то данный метод работает только при выполнении условий ОДЗ для логарифмов! Следовательно, последовательность решения подобных неравенств такая:

1) находим ОДЗ неравенства;

2) решаем неравенство, как будто ОДЗ выполнено;

3) пересекаем полученный ответ с ОДЗ и получаем итоговый ответ.

Пример.
Неравенство \((3+x-2x^2)\log_<(3x+5)>\geqslant 0\) с помощью метода рационализации можно переписать в виде: \[\begin (3+x-2x^2)(x+2-1)(3x+5-1)\geqslant 0\\ x+2>0\qquad \qquad \text<(ОДЗ)>\\ x+2\ne 1\qquad \qquad \text<(ОДЗ)>\\ 3x+5>0 \qquad \qquad \text<(ОДЗ)>\end\]

Таким образом, данное выражение имеет вид:

Тогда все неравенство примет вид:

1) Найдем ОДЗ левой части:

\[\begin x^2-3>0\\ x^2-3\ne 1\\[1ex] 3^-2>0 \end \quad \Rightarrow \quad \begin x\in(-\infty;-\sqrt3)\cup(\sqrt3;+\infty)\\ x\ne \pm 2\\ 3^>3^ <\log_32>\end \quad \Rightarrow \quad \begin x\in(-\infty;-\sqrt3)\cup(\sqrt3;+\infty)\\ x\ne \pm 2\\ x^2+2x+2>\log_32 \end\]

Решим последнее неравенство отдельно:

\[x^2+2x+2>\log_32 \quad \Rightarrow \quad x^2+2x+1>\log_32-1 \quad \Rightarrow \quad (x+1)^2>\log_32-\log_33=\log_3<\frac23>\]

2) Перейдем к решению самого неравенства на ОДЗ.

Применим метод рационализации для первого множителя (скобки) и для второго множителя (логарифма):

\((x^2+x-2-0)(x^2+x-2-(x+2))\cdot (x^2-3-1)(3^-2-1)\geqslant 0\quad \Rightarrow\)

\(\Rightarrow \quad (x^2+x-2)(x^2-4)\cdot (x^2-4)(x^2+2x+2-1)\geqslant 0\quad \Rightarrow \)

\(\Rightarrow \quad (x-1)(x+2)(x+2)(x-2)\cdot (x-2)(x+2)(x+1)^2\geqslant 0 \quad \Rightarrow\)

\(\Rightarrow \quad (x-1)(x+2)^3(x-2)^2(x+1)^2\geqslant 0\)

Решим данное неравенство методом интервалов:

3) Пересечем полученный ответ с ОДЗ и получим:

По методу интервалов:

По методу интервалов:

На ОДЗ:
исходное неравенство равносильно неравенству

По методу рационализации: на ОДЗ

\[x^4 + 2x^2 + 1 = (x^2 + 1)^2 \geqslant 0,\] тогда

\[\begin N\cdot\log_<(1 + Nx)>3\cdot\log_3(1 + x)\geqslant 1 \end\]

при любых \(N\in\mathbb.\)

ОДЗ: \[\begin 1 + Nx > 0\\ 1 + Nx\neq 1 \qquad\text<— при любых>\ N\in\mathbb\\ 1 + x > 0 \end\]

\[\begin &\dfrac<1><\log_<3>(1 + Nx)>\cdot\log_3(1 + x)^N\geqslant 1\quad\Leftrightarrow\quad\log_3(1 + x)^N\geqslant \log_<3>(1 + Nx)\quad\Leftrightarrow\\ &\Leftrightarrow\quad (1 + x)^N\geqslant (1 + Nx). \end\]

1) \(N = 1\) : \[1 + x \geqslant 1 + x\] – верно.

Решите неравенство \[x\cdot \log_<\frac13>\left(4-3\cdot 3^<^\frac1x>\right)>1\]

Теперь нужно объединить решения пунктов 1 и 2 и пересечь полученное множество с ОДЗ.
Получим окончательный ответ в неравенстве: \[x\in \left[3-\sqrt<14>;\frac43\right)\cup [3+\sqrt<14>;3+\sqrt<15>)\cup(3+\sqrt<15>;7]\]

Источник

Неравенства. Метод замены множителя (метод рационализации)

Полезный прием для решения сложных неравенств на ЕГЭ по математике – метод рационализации неравенства. Другое название — метод замены множителя. Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках о таком не написано.

Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные показательные или логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству.

Давайте для начала вспомним, что такое равносильные уравнения (или неравенства) В школьной программе этот важный вопрос почти не обсуждается. Поэтому запишем определение.

Равносильными называются уравнения, множества решений которых совпадают.

Заметим, что внешне уравнения могут быть и не похожи друг на друга.

Например, уравнения ( x − 3) 2 = 0 и x − 3 = 0 равносильны. Число 3 является единственным решением и того, и другого.

Уравнения и также равносильны. Оба они не имеют решений. Другими словами, множество решений каждого из них – пусто.

Уравнения и не являются равносильными. Решением первого уравнения является только x = 5. Решения второго – два числа: x = 5 и x = 1. Получается, что возведение обеих частей уравнения в квадрат в общем случае приводит к уравнению, неравносильному исходному.

Аналогичное определение – для неравенств.

Равносильными называются неравенства, множества решений которых совпадают.
Например, неравенства 0″ src=»https://latex.codecogs.com/png.latex?(x-1)(x-3)%3E0″ /> и 0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3Cx-1%3E%3Cx-3%3E%3E0″ /> равносильны – ведь множества их решений совпадают. В этом легко убедиться с помощью метода интервалов.

Неравенства log_<2>5″ src=»https://latex.codecogs.com/png.latex?log_%3C2%3Ex%3Elog_%3C2%3E5″ /> и 5″ src=»https://latex.codecogs.com/gif.latex?x%3E&space;5″ /> также равносильны при 0″ src=»https://latex.codecogs.com/gif.latex?x%3E&space;0″ />. Заметим, что внешне эти неравенства не похожи – одно из них логарифмическое, другое алгебраическое.

Другими словами, при x > 0 неравенства 0″ src=»https://latex.codecogs.com/png.latex?log_%3C2%3Ex-log_%3C2%3E5%3E0″ /> и 0″ src=»https://latex.codecogs.com/png.latex?x-5%3E0″ /> имеют одинаковые решения. Если какое-либо число x > 0 является решением одного из них, то оно будет и решением второго.

А это значит, что при любом x > 0 выражение будет иметь такой же знак, как и выражение x − 5. Следовательно, если в какое-либо сложное неравенство входит в качестве множителя выражение то при выполнении условия x > 0 его можно заменить на более простое x − 5 и получить неравенство, равносильное исходному.

Вот ключевой момент. На этом и основан метод рационализации – замены множителей, содержащих сложные логарифмические или показательные выражения, на более простые алгебраические множители.

Например, выражение вида , где f и g – функции от x, a – число, можно заменить на более простое ( f − g) ( a − 1) – конечно, при условии, что f(x) > 0 и g(x) > 0. Доказательство легко провести самостоятельно.

А сейчас – самое главное: волшебная таблица, позволяющая заменять сложные логарифмические (или показательные) множители в неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот увидите, она выручит вас на ЕГЭ по математике:

Конечно же, все выражения, которые содержат логарифмы, существуют при f, g, h > 0 и h ≠ 1.

Обратите внимание, что мы говорим о замене множителя в неравенствах вида Знак здесь может быть любой: >, ≥, ≤. Правая часть обязательно должна быть равна нулю. И заменяем мы именно множитель (а не слагаемое, например). Иначе ничего не получится.

Перейдем к практике – к решению задач из вариантов ЕГЭ по математике Профильного уровня.

1.

ОДЗ неравенства:

Применим метод рационализации. В соответствии с нашей таблицей, множитель заменим на (2 − x − 1)( x + 2 − 1). Множитель вида заменим на ( x + 3 − 1)(3 − x − 1). Таким образом, от логарифмического неравенства мы перешли к рациональному:

Решим его методом интервалов:

Ответ:

2.

Заметим, что выражение положительно при x ∈ ОДЗ. Умножим обе части неравенства на это выражение.
Упростим числитель правой части неравенства:

Поделим обе части неравенства на 5 x > 0:

Неравенство уже намного проще, чем исходное. Но основания степеней разные! Чтобы применить метод рационализации, нам придется представить 2 x − 1 в виде степени с основанием 3.

Неравенство примет вид:

Воспользуемся методом замены множителя. Множитель вида h f −h g можно заменить на ( h − 1) ( f − g). Да и логарифм в знаменателе можно заменить на выражение x + 1.

Оценим . Это необходимо сделать, чтобы правильно расставить точки на числовой прямой.

Ответ:

3.

Постараемся упростить это неравенство. Область допустимых значений

0;\\ x+1\neq 0. \end\right.» src=»https://latex.codecogs.com/png.latex?%5Cleft%5C%3C%5Cbegin%3Cmatrix%3E&space;x%3E0;%5C%5C&space;x+1%5Cneq&space;0.&space;%5Cend%3Cmatrix%3E%5Cright.» />Отсюда следует, что x > 0. Это хорошо, потому что при данных значениях x выражение x + 1 строго положительно, следовательно, мы можем умножить на него обе части неравенства. Да и на x 2 тоже можно умножить обе части неравенства, и тогда оно станет проще

Преобразуем числители выражений в левой и правой части и сделаем замену log₂ x = t

Теперь обе части неравенства можно сократить на 5 t > 0.

Поскольку , выражение 2 t−1 можно записать как 3 ( t−1)·log₃2

Заметим, что log₃2 − 2 t. Решим его:

Итак, t ≥ 1 или t ≤ log₃2 − 2.
Вернемся к переменной x:

или

Ответ:

4. Еще одна задача из той же серии.

Запишем ОДЗ:

Умножим обе части неравенства на 0″ src=»https://latex.codecogs.com/png.latex?log%5E%3C2%3E_%3C2%3E32x%3E0″ />. Постараемся упростить числители выражений в левой и правой части.

Поделим обе части неравенства на 0.» src=»https://latex.codecogs.com/png.latex?2%5E%3Clog_%3C2%3E(4x)%3E%3E0.» />

Хорошо бы сделать замену. Пусть log₂(4 x) = t. Тогда:

Неравенство примет вид:

Мы уже знаем, как представить число 7 в виде степени числа 2:

Применим метод рационализации.

Оценим

Применим в левой части неравенства формулу перехода к другому основанию

Поскольку 0″ src=»https://latex.codecogs.com/png.latex?(x+5)%5E%3C2%3E%3E0″ /> при x ∈ ОДЗ, а 0″ src=»https://latex.codecogs.com/png.latex?2x%5E%3C2%3E+10x+14%3E0″ /> > 0 при всех x, получим:

Посмотрим, чем поможет метод замены множителя в решении сложного показательного неравенства.

6. Решите неравенство:

Числитель дроби в левой части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим обе части неравенства на

Применяя метод рационализации, множитель вида заменяем на

Что больше? Давайте представим как логарифм с основанием

7. Теперь логарифмическое неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и область его допустимых значений мы записываем в одну систему. И решаем ее.

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что

Используем также условия

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,

Согласно методу замены множителя, выражение заменим

8. А теперь неравенство с ловушкой. Мы надеемся, что вы помните — нельзя извлекать корень из неравенства.

Извлекать корень из неравенства нельзя! Можно перенести все в левую часть неравенства и разложить на множители как разность квадратов:

Применим формулы разности и суммы логарифмов, следя за областью допустимых значений. Все выражения под логарифмами в исходном неравенстве должны быть положительны.

Посмотрим на второе и третье неравенства системы. Поскольку х+5 положительно, то и выражение должно быть положительно.

Заметим, что решения неравенства — это все числа, кроме

По методу рационализации, каждый из множителей вида заменяем на

Просто равносильные преобразования. Выражение положительно всегда — так как в уравнении дискриминант отрицателен. Осталось применить метод интервалов.

Источник