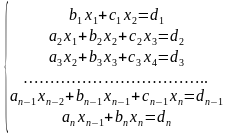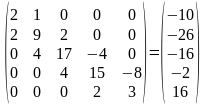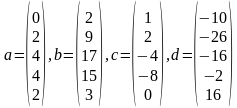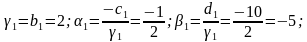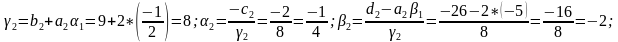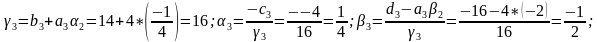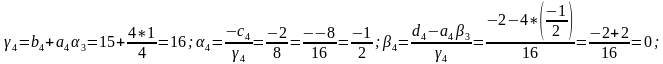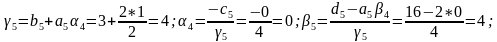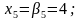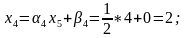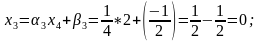что такое метод прогонки
Линейные уравнения. Решение систем линейных уравнений. Метод прогонки.
Метод прогонки (алгоритм Томаса) используют для решения СЛУ типа Ax=F, где A — трёхдиагональная матрица. Это вариант метода последовательного исключения неизвестных.
Система уравнений Ax=F равноценна соотношению:
Метод прогонки базируется на предположении, что неизвестные, которые необходимо найти, связаны соотношением:
Выразим xi-1 и xi через xi+1, подставим в уравнение, используя это соотношение, (1):
где Fi — правая часть i-го уравнения.
Это соотношение выполняется не завися от решения, если потребовать:


Получаем из 1-го уравнения:

После того, как нашли прогоночные коэффициенты α и β, используем уравнение (2) и получим решение системы. Причем,

Еще одним вариантом объяснения смысла метода прогонки является такой вариант: преобразуем уравнение (1) к равнозначному ему уравнению:
c надиагональной (наддиагональной) матрицей:
Рассчеты проводим в 2 этапа. На 1-ом этапе вычисляем компоненты матрицы C′i и вектора F′, начиная с i=2 до i=n:
На 2-ом этапе, для i=n,n−1,…,1 вычисляем решение:
Для применимости формул метода прогонки достаточно свойства строгого диагонального преобладания у матрицы A.
«Метод прогонки»
Содержимое разработки
Государственное бюджетное профессиональное образовательное учреждение
Московской области «Подольский колледж имени А.В. Никулина»
по дисциплине «ЕН Математика»
по теме: «Метод прогонки»
для студентов II курса
15.02.15 Технология металлообрабатывающего производства
Преподаватель первой квалификационной категории
Носова Оксана Васильевна
Специальность: 15.02.15 Технология металлообрабатывающего производства
Дисциплина: ЕН Математика
Тема: Метод прогонки.
Цель: изучить точный метод решения систем линейных алгебраических уравнений — метод прогонки для решения систем линейных уравнений с трехдиагональными матрицами коэффициентов.
формирование представлений о системах линейных уравнений с трехдиагональной структурой и методе прогонки,
формирование умений применять знания при решении задач;
способствовать развитию умений обучающихся обобщать полученные знания, проводить анализ, сравнение, делать необходимые выводы;
способствовать развитию логического мышления;
способствовать развитию вычислительных навыков при решении задач по специальности;
способствовать овладению обучающимися необходимыми навыками самостоятельной учебной деятельности, формирование познавательной активности и умения принимать решения и отвечать за принятые решения.
Тип урока: урок теоретического обучения
1) словесные (лекция);
2) наглядные (мультимедийная презентация, опорный конспект);
3) практические (решение задач).
-Решение систем линейных уравнений
Приветствие. Раздача опорных конспектов
На прошлом занятии мы рассмотрели решение СЛАУ с помощью правила Крамера. Выяснили, что не смотря на свое изящество и простоту, он редко применяется в вычислительной практике решения систем.
Почему? (ответы обучющихся)
Верно. Так, например, если в системе 10 уравнений, то сколько требуется вычислить определителей? (ответы обучющихся)
Верно. Если учесть, что в системах, связанных с реальными практическими задачами, количество неизвестных бывает весьма большим, то станет понятно, что метод решения по правилу Крамера для таких систем, скорее всего окажется неприемлемым.
На этом и следующих занятиях мы продолжим изучать методы решения СЛАУ. И сегодня мы познакомимся с одним из методов, который реально используется в вычислительной практике. Этот метод находит широкое применение по двум причинам. Во-первых, он прост и эффективен; во-вторых, системы уравнений, к которым он применим, довольно часто встречаются в задачах математического моделирования. Этот метод называется методом прогонки.
И немного из истории решения СЛАУ нам расскажет _______________________(ФИ).
Задача остальных – при прослушивании сообщения, выяснить, для каких матриц применим метод прогонки.
(сообщение студента) (3 – 4) мин
Итак, для каких же матриц применим метод прогонки.
Верно, для трехдиагональных мартиц.
Во многих задачах матрицы коэффициентов системы линейных алгебраических уравнений являются слабозаполненными. Если ненулевые элементы матрицы коэффициентов расположены только на главной диагонали и на нескольких побочных диагоналях, то такие матрицы называют матрицами ленточной структуры. Рассмотрим частный случай матрицы коэффициентов ленточной структуры — матрицу с трехдиагональной структурой, которая имеет вид:
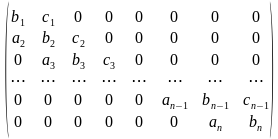
и соответствующую ей систему линейных алгебраических уравнений:
Для решения систем линейных алгебраических уравнений с трехдиагональной матрицей был разработан метод прогонки – метод последовательного исключения неизвестных,состоящий из двух этапов: этапа прямой прогонки, основанного на вычислении прогоночных коэффициентов
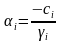
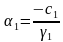
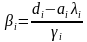
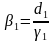
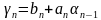
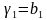
и этапа обратной прогонки, основанного на использовании прогоночных коэффициентов для нахождения неизвестных, начиная с n-го неизвестного
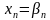
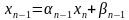
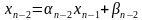
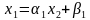
Условия на коэффициенты системы (1), обеспечивающие успешное нахождение всех неизвестных (ни один из знаменателей 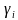
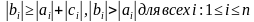
Это условие называют условием диагонального преобладания. Имеется ввиду, что модули элементов, стоящих на главных диагоналях, не меньше суммы модулей остальных элементов строки матрицы системы.
-Решение систем линейных уравнений
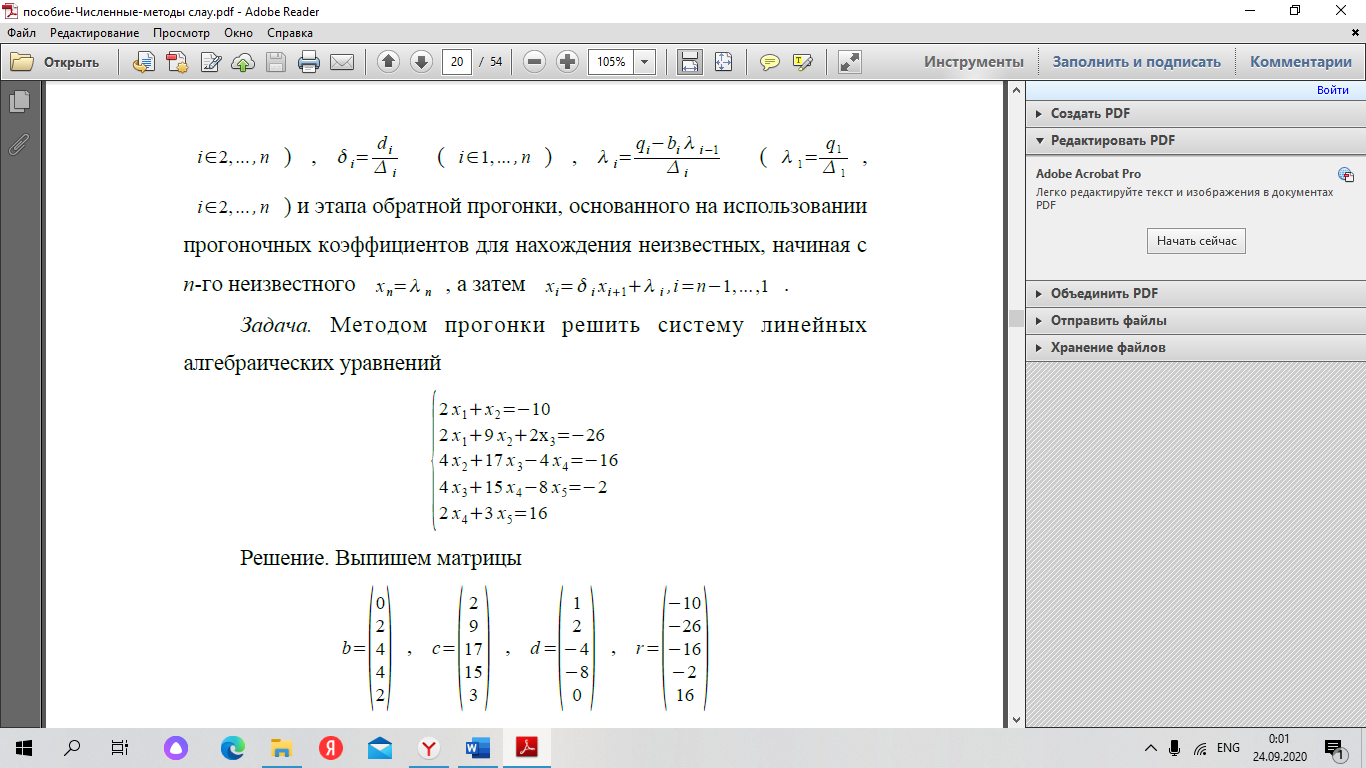
Задача 1. Методом прогонки решить систему линейных алгебраических уравнений (условие есть на опорном конспекте)
Решение. Запишем коэффициенты в матричном виде
Для удобства выпишем матрицы
Прямая прогонка. Прямую прогонку осуществляем вычислением пргоночных коэффициентов по приведенным ранее формулам
Обратная прогонка. Найдем решение системы линейных алгебраических уравнений
Проверка найденных решений (подставить в уравнения системы)
Подведем итог нашего занятия.
Перед вами матрица. Кстати, какая это матрица? (ответы обучающихся)
Под каждым ненулевым элементом матрицы скрыт вопрос или предложение, которое необходимо продолжить. Вы выбираете элемент матрицы и отвечаете на соответствующий вопрос (студенты по очереди выбирают вопросы)
3 – Сегодня на уроке я научился…
1 – Мне было сложно (не сложно) …
2 – Трехдиагональной матрицей называется…
-1 – В чем заключается метод прогонки?
5 – Материал урока мне был … (понятен/непонятен, интересен/ неинтересен).
Домашнее задание. Решить систему методом Крамера и методом прогонки.
Матрица с трехдиагональной структурой:
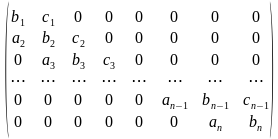
Соответствующая ей система линейных алгебраических уравнений:
Алгоритм метода прогонки:
1.Прямая прогонка (вычисление прогоночных коэффициентов)
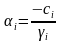
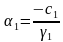
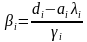
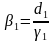
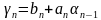
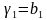
2.Обратная прогонка (нахождение неизвестных)
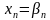
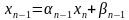
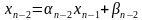
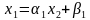
Задача 1. Методом прогонки решить систему линейных алгебраических уравнений (условие есть на опорном конспекте)
Решение. Запишем коэффициенты в матричном виде
Решение систем линейных алгебраических уравнений
Решение систем линейных
алгебраических уравнений
| Сайт: | Электронные курсы ТПУ |
| Курс: | Информационные технологии 1 |
| Книга: | Решение систем линейных алгебраических уравнений |
| Напечатано:: | Гость |
| Дата: | Понедельник, 22 Ноябрь 2021, 23:18 |
Оглавление
Решение систем линейных алгебраических уравнений
Системы линейных алгебраических уравнений (СЛАУ) появляется почти в каждой области прикладной математики. В некоторых случаях эти СЛАУ непосредственно составляют ту задачу, которую необходимо решить, в других случаях задача сводится к решению такой системы. Примерами таких задач являются системы нелинейных уравнений, дифференциальных уравнений в частных производных, задачи аппроксимации и интерполяции и др. Решение СЛАУ является одной из самых распространенных и важных задач вычислительной математики.
Систему n линейных алгебраических уравнений с n неизвестными запишем как:

| A = |  |  |
Систему можно записать в матричном виде A×X=B, где X – вектор-столбец неизвестных; B – вектор-столбец правых частей.
Рассмотрим некоторые специальные виды матриц :
|
|
Здесь С – симметричная матрица (ее элементы расположены симметрично относительно главной диагонали, т. е. aij=aji ); T – верхняя треугольная матрица с равными нулю элементами, расположенными ниже диагонали; К – клеточная матрица (ее ненулевые элементы составляют отдельные группы-клетки); Д – ленточная матрица (ее ненулевые элементы составляют «ленту», параллельную диагонали; в данном случае данная матрица Д одновременно является также трехдиагональной).
Методы решения СЛАУ делятся на две группы – прямые и итерационные.
1. Прямые методы
Прямые методы используют заранее известное, зависящее от n, количество соотношений (формул) для вычисления неизвестных. К ним относятся правило Крамера, метод Гаусса (или метод последовательного исключения неизвестных), метод Гаусса с выбором главного элемента, метод прогонки (частный случай метода Гаусса для СЛАУ с трехдиагональной матрицей), метод Жордана (часто используется для нахождения обратной матрицы), метод квадратного корня (применяется тогда, когда матрица системы является симметричной), клеточные методы (используются для решения больших СЛАУ, когда матрица и вектор правых частей целиком не помещаются в оперативной памяти ЭВМ) и др. Алгоритмы этих методов сравнительно просты и наиболее универсальны, т. е. пригодны для решения широкого класса СЛАУ. К недостаткам таких методов относится требование хранения в оперативной памяти ЭВМ сразу всей исходной матрицы, и, следовательно, при больших значениях n используется большой объем памяти. Прямые методы не учитывают конкретный вид матрицы или ее структуру, т. е. при большом числе нулевых элементов в ленточных или клеточных матрицах эти элементы занимают место в памяти ЭВМ, и над ними проводятся практически бесполезные арифметические операции. Кроме того, существенным недостатком прямых методов является увеличение погрешностей в процессе получения решения, т. к. вычисления на последующем этапе используют результаты предыдущих операций, полученных, в свою очередь, с какой-то погрешностью. Особенно актуальным становится вышеуказанное обстоятельство для больших СЛАУ вследствие резкого увеличения общего количества числа арифметических действий, а также для плохо обусловленных СЛАУ из-за их чувствительности к погрешностям.
Поэтому прямые методы применяются для относительно небольших (n x1 + x2 + x3 – x4 = 2 ;
Для удобства обозначим уравнения буквами и будем выписывать только коэффициенты при неизвестных и свободные члены уравнений. Тогда исходная СЛАУ примет вид
Исключая члены, содержащие x1, получим
После исключения членов с x2 имеем
Исключения членов с x3 дает
Продолжая аналогичные действия с последним рядом, получим
Возвращаясь к общепринятой форме уравнений, запишем
Обратный ход метода Гаусса состоит в последовательном вычислении исходных неизвестных. Из последнего уравнения находим единственное неизвестное x4, подставляя значение x4 в третье уравнение, x3 – во второе и т. д., находим решение заданной СЛАУ:
Аналогично строится алгоритм для СЛАУ с произвольным числом уравнений. Необходимо помнить, что при решении СЛАУ может потребоваться операция перестановок уравнений (т. е. перестановки соответствующих коэффициентов), служащая для предотвращения деления на нулевой элемент.
Вычисленное по методу Гаусса решение X * для СЛАУ, записанной в матричном виде A × X = B, отличается от точного решения X из-за погрешностей округления, связанных с ограниченностью разрядной сетки ЭВМ. Существуют две величины, характеризующие степень отклонения полученного решения X * от точного X. Одна из них – погрешность Е, равная разности этих значений: E = X – X * .
Реализация метода на языке Паскаль
Потребуется описание используемых типов для расширенной матрицы коэффициентов и для вектора значений переменных:
type mat=array[1..20,1..21] of real;
vec=array[1..20] of real;
var n:integer;
a:mat; x:vec;
Ввод матрицы наиболее эффективно реализовать из файла данных. Для этого потребуется файловый тип и файловая переменная
var f:text;
В основной части программы ввод можно организовать следующим образом:
Write(‘Введите число уравнений N = ‘); readln( n );
reset(f);
for i:=1 to n do
begin
for j:=1 to n+1 do read(f,a[i,j]);
readln(f);
close(f);
Прямой ход метода Гаусса (формирование треугольной матрицы коэффициентов) может выглядеть так:
for k:=1 to n do
begin
s:=a[k,k];j:=k;
for i:=k+1 to n do
begin
r:=a[i,k];
if abs(r)>abs(s) then
begin
s:=r; j:=i;
if s=0 then
begin
halt;
if j<>k then
for i:=k to n+1 do
begin
for j:=k to n+1 do a[k,j]:=a[k,j]/s;
for i:=k+1 to n do
begin
r:=a[i,k];
for j:=k to n+1 do
a[i,j]:=a[i,j]-a[k,j]*r;
Обратный ход метода Гаусса (вычисление вектора значений переменных) может выглядеть так:
if s<>0 then
for i:=n downto 1 do
begin s:=a[i,n+1];
for j:=i+1 to n do s:=s-a[i,j]*x[j];
Остаётся только вывести результат и сделать проверку.
3. Метод прогонки
Он является модификацией метода Гаусса для частного случая разреженных систем – системы уравнений с трехдиагональной матрицей. Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений.
Запишем систему уравнений в виде
Метод прогонки состоит из двух этапов – прямой прогонки (аналога прямого хода метода Гаусса) и обратной прогонки (аналога обратного хода метода Гаусса). Прямая прогонка состоит в том, что каждое неизвестное xi выражается через xi+1 с помощью прогоночных коэффициентов ai, bi:
Приравнивая коэффициенты в обоих выражениях для x1,получаем
Из второго уравнения системы (8.3) выразим x2 через x3, заменяя x1 по формуле (8.4):
Аналогично можно вычислить прогоночные коэффициенты для любого номера i:
4. Итерационные методы
К таким методам относятся метод Якоби (метод простой итерации, или метод одновременных смещений), метод Зейделя (Гаусса-Зейделя, или метод последовательных смещений), метод верхней релаксации.
где Ea – заданная абсолютная погрешность;
Eо – заданная относительная погрешность.
Преимущества данных методов по сравнению с прямыми заключаются в следующем:
1. В ряде случаев удается хранить в памяти ЭВМ не всю матрицу системы, а лишь несколько векторов (см. матрицы Т, К, Д).
Для реализации итерационного метода исходную СЛАУ (8.1) обычно приводят к виду :
5. Метод Зейделя
Этот метод является итерационным. На каждой итерации уточняются значения переменных. Система сходится, если на главной диагонали матрицы коэффициентов расположены максимальные элементы. В противном случае необходимо провести эквивалентные преобразования (перестановка строк и др.).
Систему (8.9) приведём к виду
Левую часть уравнений будем считать новыми (последующими) значениями переменных, а xi в правой части – предыдущими значениями переменных. Первоначально массив X имеет нулевые значения. Затем на каждой итерации вычисляется S – добавка для каждого xi, которая приближает его к искомому значению. Процесс продолжается до тех пор, пока добавка для каждого xi будет меньше заданной погрешности вычислений.
Реализация метода на языке Паскаль
Ввод данных рекомендуется организовать так же, как и в методе Гаусса. Далее приводится возможный вариант реализации метода:
for k:=1 to m do
begin
for i:=1 to n do
begin
s:=a[i,n+1];
for j:=1 to n do s:=s-a[i,j]*x[j];
s:=s/a[i,i];
x[i]:=x[i]+s;
if abs(s)>e then z:=0
if z<>0 then Break;
Здесь m – максимальное число итераций (для избежания бесконечного цикла); z – переменная, обнуляющаяся, если хотя бы одна из переменных отличается от предыдущего значения более чем на Е, и содержащая число итераций, если система сошлась.
Остаётся только вывести результат и сделать проверку.
6. Метод простых итераций
Метод простых итераций немного отличается от метода Зейделя. Здесь имеется два вектора переменных: с предыдущими значениями X0 и с последующими значениями X1. В конце каждой итерации производится переприсвоение значений из последующих в предыдущие:
for k:=1 to m do
begin
for i:=1 to n do
begin
s:=a[i,n+1];
for j:=1 to n do s:=s-a[i,j]*X0[j];
s:=s/a[i,i];
X1[i]:=X0[i]+s;
if abs(s)>e then z:=0
if z<>0 then Break
else
for i:=1 to n do X0[i]:=X1[i];
7. Вывод результатов и проверка
Чтобы проверить, правильно ли решена система уравнений, нужно подставить найденные значения x в левую часть каждого уравнения и найти относительную погрешность между полученным значением и правой частью этого уравнения:
for i:=1 to n do
writeln(‘X[,i,]=’,X[i]);
writeln(‘Проверка:’);
for i:=1 to n do
begin
for j:=1 to n do s:=s+a[i,j]*X[j];
write(‘Уравнение ’,i,‘ ’,s,‘ = ’,a[i,n+1]);
writeln(‘ Погрешность ’, abs((s-a[i,n+1])/s));
Замечание. При решении системы методом Гаусса перед проверкой нужно заново произвести ввод исходной матрицы из файла данных. Это нужно сделать потому, что исходная матрица A была преобразована в треугольную при прямом проходе и теперь требуется перечитать её исходное состояние для проведения проверки.