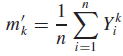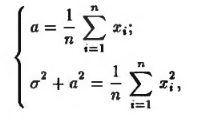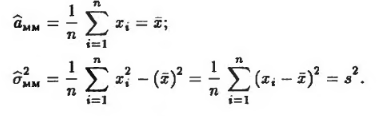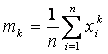что такое метод моментов
Особенности метода моментов.
Ключевые вопросы: определение, предпосылки модели, понятие и формулы моментов, алгоритм расчёта оценок, применение в нормальном распределении, дискуссия о типе и количестве моментов, достоинства и недостатки подхода.
Метод моментов – один из наиболее известных и популярных методов статистического оценивания параметров вероятностных распределений.
Основные предпосылки модели метода моментов следующие:
Суть метода моментов заключается в вычислении того количества теоретических и выборочных моментов случайной величины, которое равно числу исследуемых нами параметров. После вычисления соответствующие друг другу теоретические и выборочные моменты приравниваются, и исходя из получившегося уравнения осуществляется вычисление оценки параметра.
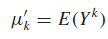
Формула выборочных моментов выглядит так: где m’k – есть k-й выборочный момент величины Y.
После этого приравниванием μ’k = m’k добиваемся вычисления значений параметров.
Рассмотрим в качестве примера нормальное распределение. Нахождение оценок параметров по методу моментов выглядит следующим образом.
Следует заметить, что в уравнения также допустимо включать и такие экзотические виды моментов, как асимметрию и эксцесс, но это необходимо только в специализированных исследованиях. Статистическая практика чаще всего не выходит за рамки обозначенного выше алгоритма, поскольку число подлежащих исследованию параметров обыкновенно не превышает 4.
В другом изложении:
Введём сначала следующие определения:
Определение 9. Начальный момент порядка k случайной величины x определяется равенством: mk = M(x k ).
В частности, m1 = M(x) – обычное мат. ожидание, m2 = M(x 2 ).
Определение 10. Центральный момент порядка k случайной величины x определяется равенством: ak = M((x–Mx) k ).
В частности, a2 = D(x) – дисперсия случайной величины.
Эти моменты называют теоретическими. По данным наблюдений можно вычислить соответствующие эмпирические моменты:
Определение 11. Начальный эмпирический момент порядка k случайной величины x определяется равенством
В частности, 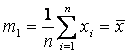
Определение 12. Центральный эмпирический момент порядка k случайной величины x определяется равенством:
В частности, 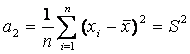
Метод моментов построения точечных оценок неизвестных параметров состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же распределения.
Пусть даны: случайная величина ξ, выборка объема n x1, x2,…, xn. Необходимо построить оценки неизвестных параметров q * 1,q * 2,…,q * k. Описание метода моментов (ММ) разобьём на этапы:
1. Выписываем первые к моментов μ1, μ2, … μn
3. Составляем систему уравнений μi = mi и решаем ее относительно неизвестных параметров.
Замечание 1. Иногда вместо начальных моментов μi, mi удобно использовать центральные моменты αi, ai.
Замечание 2. Если на третьем этапе получилась неразрешимая система, то на первом шаге надо добавить новые моменты.
Найдем методом моментов оценки параметров нескольких важнейших распределений.
Метод моментов
Ме́тод моме́нтов — метод оценки неизвестных параметров распределений в математической статистике и эконометрике, основанный на предполагаемых свойствах моментов(Пирсон, 1894 г.). Идея метода заключается в замене истинных соотношений выборочными аналогами.
Содержание
Сущность метода
Пусть случайная величина (вектор, матрица и т. д.) X имеет некоторое распределение 



Пусть 
причем в данном представлении (когда справа от равенства — ноль) достаточно использовать просто суммы вместо средних.
Оценки, получаемые из решения этой системы уравнений (выборочных условий на моменты), называются оценками метода моментов. Название метода связано с тем, что чаще всего в качестве функций 
Если моментные функции непрерывны, то оценки метода моментов состоятельны.
Частные случаи
Некоторые классические методы оценки регрессионных моделей можно представить как частные случаи метода моментов. Например, если линейная регрессионная модель 

Следовательно, в этом случае оценка метода моментов будет совпадать с оценкой метода наименьших квадратов
Таким образом, МНК является частным случаем метода моментов, когда выполняется условие ортогональности регрессоров и случайных ошибок
Рассмотрим другой случай, когда имеются некоторые переменные z, ортогональные случайным ошибкам линейной регрессионной модели, то есть 
Следовательно оценка метода моментов будет совпадать с оценкой метода инструментальных переменных: 
Таким образом, метод инструментальных переменных является частным случаем метода моментов, когда выполнено условие ортогональности инструментов и случайных ошибок модели.
Обобщенный метод моментов
Метод моментов может быть обобщен на случай когда количество условий на моменты превышает количество параметров, которые необходимо оценить. В этом случае, очевидно однозначного решения задача не имеет (в общем случае). В таком случае решается задача на минимизацию некоторого функционала, характеризующего интегральную степень соблюдения условий на моменты.
Пусть 
где W — некоторая симметрическая положительно определенная матрица.
Весовая матрица теоретически может быть произвольной (с учетом ограничения положительной определенности), однако, доказано, что наиболее эффективными являются GMM-оценки с весовой матрицей, равной обратной ковариацинной матрице моментных функций 
Пример
Пусть 



Тогда оценки метода моментов удовлетворяют системе уравнений:

Преимущества и недостатки метода
В известной мере, при оценке параметров из известного семейства вероятностных распределений, этот метод упраздняется Фишеровским методом максимального правдоподобия, так как максимально правдоподобная оценка имеет большую вероятность оказаться ближе к истинному значению оцениваемой величины.
Тем не менее, в некоторых случаях, например, как выше в случае Гамма-распределения, использование метода максимального правдоподобия требует использования компьютеров в то время, как метод моментов может быть быстро и легко реализован вручную.
Оценки, полученные методом моментов, могут быть использованы как первое приближение для метода максимума правдоподобия. Дальнейшее улучшение оценок может быть получено с использованием метода Ньютона-Рафсона.
В некоторых случаях, редких при больших объемах данных и более частых при малом их количестве, оценки, даваемые методом моментов могут оказаться вне допустимой области. Такая проблема никогда не возникает в методе максимального правдоподобия. Также, оценки по методу моментов не обязательно оказываются достаточной статистикой, то есть, они иногда извлекают из данных не всю имеющуюся в них информацию.
См. также
Полезное
Смотреть что такое «Метод моментов» в других словарях:
метод моментов — momentų metodas statusas T sritis fizika atitikmenys: angl. method of moments; moments method vok. Momentenmethode, f rus. метод моментов, m pranc. méthode de moments, f … Fizikos terminų žodynas
Метод моментов нахождения оценок — в математической статистике это способ построения оценок, основанный на уравнивании теоретических и выборочных моментов. (Пирсон 1894г.) Содержание 1 Определение 2 Замечания … Википедия
Обобщенный метод моментов — (ОММ, GMM Generalized Method of Moments) метод, применяемый в математической статистике и эконометрике для оценки неизвестных параметров распределений и эконометрических моделей, являющийся обобщением классического метода моментов. Метод был… … Википедия
Метод инструментальных переменных — (ИП, IV Instrumental Variables) метод оценки параметров регрессионных моделей, основанный на использовании дополнительных, не участвующих в модели, так называемых инструментальных переменных. Метод применяется в случае, когда факторы… … Википедия
Метод максимального правдоподобия — или метод наибольшего правдоподобия (ММП, ML, MLE Maximum Likelihood Estimation) в математической статистике это метод оценивания неизвестного параметра путём максимизации функции правдоподобия[1]. Основан на предположении о том, что… … Википедия
метод распределения моментов — Метод расчёта сложных статически неопределимых рам, при котором первоначально неуравновешенные моменты в узлах уравновешиваются по методу последовательных приближений с помощью коэффициентов распределения моментов [Терминологический словарь по… … Справочник технического переводчика
МОМЕНТОВ МЕТОД — метод определения распределения вероятностей по его моментам. В теоретич. отношении М. м. основан на единственности решения моментов проблемы:если нек рые постоянные, то при каких условиях существует единственное распределение такое, что суть… … Математическая энциклопедия
МЕТОД РАСПРЕДЕЛЕНИЯ МОМЕНТОВ — метод расчёта сложных статически неопределимых рам, при котором первоначально неуравновешенные моменты в узлах уравновешиваются по методу последовательных приближений с помощью коэффициентов распределения моментов (Болгарский язык; Български)… … Строительный словарь
МЕТОД — (от греч. methodos путь, способ исследования, обучения, изложения) совокупность приемов и операций познания и практической деятельности; способ достижения определенных результатов в познании и практике. Применение того или иного М. определяется… … Философская энциклопедия
МЕТОД СВОБОДНЫХ АССОЦИАЦИЙ — (лат. associatio соединение, присоединение) исследовательский, диагностический и терапевтический прием психоанализа. Основан на использовании феномена ассоциативности мышления для познания глубинных (преимущественно бессознательных) психических… … Новейший философский словарь
Метод моментов нахождения оценок
Содержание
Определение
Пусть 





где 
называется оценкой параметра 
Замечания
то есть оценка методом моментов получается путём приравнивания теоретического среднего g(X) с выборочным средним.
Состоятельность метода
Если 
Пример

Тогда оценки метода моментов удовлетворяют системе уравнений:


Преимущества и недостатки метода
В известной мере, при оценке параметров из известного семейства вероятностных распределений, этот метод упраздняется Фишеровским методом максимального правдоподобия, т.к. максимально правдоподобная оценка имеет большую вероятность оказаться ближе к истинному значению оцениваемой величины.
Тем не менее, в некоторых случаях, например, как выше в случае Гамма-распределения, использование метода максимального правдоподобия требует использования компьютеров в то время, как метод моментов может быть быстро и легко реализован вручную.
Оценки, полученные методом моментов, могут быть использованы как первое приближение для метода максимума правдоподобия. Дальнейшее улучшение оценок может быть получено с использованием метода Ньютона-Рафсона.
В некоторых случаях, редких при больших объемах данных и более частых при малом их количестве, оценки, даваемые методом моментов могут оказаться вне допустимой области. Такая проблема никогда не возникает в методе максимального правдоподобия. Также, оценки по методу моментов не обязательно оказываются достаточной статистикой, то есть, они иногда извлекают из данных не всю имеющуюся в них информацию.
См. также
Полезное
Смотреть что такое «Метод моментов нахождения оценок» в других словарях:
МОМЕНТОВ МЕТОД — метод определения распределения вероятностей по его моментам. В теоретич. отношении М. м. основан на единственности решения моментов проблемы:если нек рые постоянные, то при каких условиях существует единственное распределение такое, что суть… … Математическая энциклопедия
Моменты случайной величины — Момент случайной величины числовая характеристика распределения данной случайной величины. Содержание 1 Определения 2 Замечания … Википедия
t-критерий Стьюдента — t критерий Стьюдента общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t критерия связаны с проверкой равенства средних… … Википедия
Среднеквадратическое отклонение — (синонимы: среднеквадратичное отклонение, квадратичное отклонение; близкие термины: стандартное отклонение, стандартный разброс) в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины … Википедия
Статистика — Гистограмма (метод графических изображений) У этого термина существуют и другие значения, с … Википедия
U-критерий Манна — U критерий Манна Уитни (англ. Mann Whitney U test) статистический критерий, используемый для оценки различий между двумя независимыми выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять… … Википедия
Генеральная совокупность — Генеральная совокупность, генеральная выборка (от лат. generis общий, родовой)(в англ. терминологии population) совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.… … Википедия
Конспект лекций Глазова / 12.2. Метод моментов
12.2. Метод моментов.
где 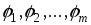

— статистический момент k-го порядка. Разумеется, можно выражать оцениваемые параметры через центральные моменты или, смешанно, через начальные и центральные.
Пример 1. Класс распределений

с одним параметром 



Пример 2. Тот же класс распределений с другим параметром:

Выражение параметра через момент: 

следовательно, оценки по методу моментов
Пример 4. Класс 




Сравнивая с примером 3, видим, что известность или неизвестность 
Пример 5. Класс 
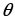


Сравнивая с примером 3, видим, что оценка с. к. о. по методу моментов зависит от того, известно mx, или нет.
Свойства оценок по методу моментов (ММ-оценок).
1) Метод прост, при его реализации как правило не возникает каких-либо математических проблем.
2) При довольно общих условиях ММ-оценки асимптотически нормальны, что облегчает построение интервальных оценок (см. п. 13) и испытание гипотез о параметрах распределений.
3) В общем случае ММ-оценки имеют смещение, порядок относительного смещения при больших n:

Часто (но не всегда) смещение этих оценок можно устранить с помощью простых поправок, т. е. образовать новые оценки (уже не ММ-оценки), не имеющие смещения (примеры устранения смещения приведены ниже).
4) Порядок дисперсии ММ-оценки при больших n:
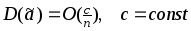
5) ММ-оценки состоятельны.
6) Р. Фишер в 1921 г. показал, что ММ-оценки чаще всего не эффективны, и даже асимптотически не эффективны. Он рассмотрел большое число практически используемых распределений и показал, что нормальное распределение в этом смысле исключение: его ММ-оценки эффективны или асимптотически эффективны, а ММ-оценки параметров подавляющего большинства других распределений имеют эффективность и асимптотическую эффективность значительно меньшие единицы.
Смещение и эффективность ММ-оценок на примерах.
Пример 1. Оценивание математического ожидания. Пусть единственным неизвестным параметром распределения является математическое ожидание mх. ММ-оценка этого параметра
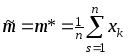
Как неоднократно показано выше, эта оценка состоятельна и несмещенна. Ее эффективность зависит от класса распределений генеральной СВ, например, как показано выше, она эффективна для нормального, экспоненциального, биномиального, пуассоновского распределений.

ее математическое ожидание

следовательно, она несмещенная; ее эффективность зависит от класса распределений генеральной СВ.
Оценка 

В соответствии с (6.3.4) можно записать:


Найдем каждый член в правой части по отдельности. Имеем:



Т. к. xk и xs при 
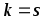
Подставляя это в (12.2.4), получаем

Подставляя этот результат и (12.2.3) в выражение (12.2.2), получаем

Т. о. оценка 


т.е. она асимптотически несмещенная.
Из (12.2.5) видно, что из 

имеет математическое ожидание

и, значит, несмещенная.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.