что такое метод интерполяции
Интерполяция и дискретизация, зачем они нужны при проективном преобразовании изображения?
Привет, Хабр! Сегодня мы очень подробно расскажем о неочевидных моментах в такой, казалось бы, простой операции: исправлении проективных искажений на изображении. Как это часто оказывается в жизни, нам пришлось выбирать, что важнее: качество или скорость. И чтобы достичь некого баланса мы вспомнили об алгоритмах, которые активно исследовали еще в 80-90-е годы в рамках задачи рендеринга структур, и с тех пор редко вспоминали в контексте обработки изображений. Если интересно, заглядывайте под кат!
Модель камеры обскуры, которая на практике неплохо приближает и короткофокусные камеры мобильных телефонов, подсказывает нам что при поворотах камеры изображения плоского объекта связаны между собой проективным преобразованием. Общий вид проективного преобразования такой:
где матрица проективного преобразования,
и
координаты на исходном и преобразованном изображениях.
Геометрическое преобразование изображений
Проективное преобразование изображения — это одно из возможных геометрических преобразований изображений (таких преобразований, при которых точки исходного изображения переходят в точки конечного изображения согласно определенному закону).
Чтобы разобраться в том, как именно следует решать задачу геометрического преобразования цифрового изображения, нужно учитывать модель его формирования из оптического изображения на матрице камеры. Согласно Г. Уолбергу [1] наш алгоритм должен аппроксимировать следующий процесс:
Интерполяция
Здесь мы рассмотрим только простые виды интерполяции — те, которые можно представить в виде свертки изображения с интерполяционным ядром. В контексте обработки изображений лучше бы подошли алгоритмы адаптивной интерполяции, которые сохраняют четкие границы объектов, однако их вычислительная сложность существенно выше и потому нам не интересна.
Будем рассматривать следующие методы интерполяции:
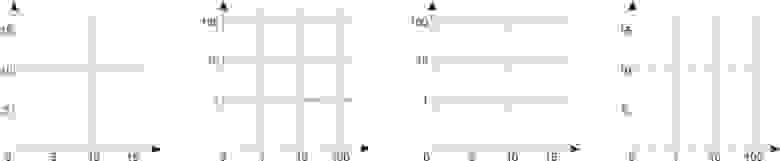
Поэтому сравним Фурье-спектры наших ядер интерполяции с фильтром низких частот (на рисунках представлены для одномерного случая).
И что, можно просто взять ядро с достаточно хорошим спектром и получить относительно точные результаты? На самом деле нет, потому что выше мы сделали два допущения: о том что есть значение пикселя изображения и о непрерывности этого изображения. При этом ни то ни другое не является частью хорошей модели формирования изображения, ведь датчики на матрице камеры не точечные, а на изображении очень много информации несут границы объектов — разрывы. Поэтому, увы, следует понимать, что результат интерполяции всегда будет отличаться от оригинального оптического изображения.
Но делать что-то все-таки нужно, поэтому коротко опишем достоинства и недостатки каждого из рассматриваемых методов с практической точки зрения. Проще всего это увидеть при увеличении масштаба изображения (в данном примере — в 10 раз).
Интерполяция по ближайшему пикселю
Билинейная интерполяция
Бикубическая интерполяция
Интерполяция B-сплайном
Итерполяция на основе кубического Эрмитового сплайна
Сравним эти методы также по числу обращений в память (числу пикселей исходного изображения для интерполяции в одной точке) и по числу операций умножения на точку.
| Интерполяция | Число пикселей | Число умножений |
| По ближайшему | 1 | 0 |
| Билинейная | 4 | 8 |
| Бикубическая | 16 | 68 |
| B-сплайн | 16 | 68 |
| Эрмитов сплайн | 36 | 76 |
Видно, что последние 3 способа существенно более вычислительно затратные, чем первые 2.
Дискретизация
Это тот самый шаг, которому совершенно незаслуженно уделяется очень мало внимания в последнее время. Самый простой способ произвести проективное преобразование изображения — оценить значение каждого пикселя конечного изображения по значению, которое получается при обратном преобразовании его центра на плоскость исходного изображения (с учетом выбранного метода интерполяции). Такой подход назовем попиксельной дискретизацией. Однако в областях, где изображение сжимается, это может привести к существенным артефактам, вызванным проблемой наложения спектров при недостаточной частоте дискретизации.
Наглядно продемонстрируем артефакты сжатия на образце паспорта РФ и отдельном его поле — место рождения (гор. Архангельск), сжатым с помощью попиксельной дискретизации или алгоритма FAST, который мы рассмотрим ниже.
Видно, что текст на левом изображении стал нечитаемым. Правильно, ведь мы берем всего одну точку из целого региона исходного изображения!
Раз нам не удалось выполнить оценку по одному пикселю, то почему бы не выбрать больше отсчетов на пиксель, а полученные значения усреднить? Такой подход называется суперсемплинг. Он действительно увеличивает качество, но вместе с тем и вычислительная сложность возрастает пропорционально числу отсчетов на пиксель.
Более вычислительно эффективные методы были придуманы в конце прошлого века, когда в компьютерной графике решалась задача рендеринга текстур, наложенных на плоские объекты. Одним из таких методов является преобразование с помощью mip-map структуры. Mip-map это пирамида изображений состоящая из самого исходного изображения, а также его копий уменьшенных в 2, 4, 8 и так далее раз. Для каждого пикселя мы оцениваем, какая степень сжатия для него характерна, и в соответствие с этой степенью выбираем нужный уровень из пирамиды, в качестве исходного изображения. Есть разные способы оценивать подходящий уровень mip-map (см. подробнее [2]). Здесь мы воспользуемся методом, на основе оценки частных производных по известной матрице проективного преобразования. Однако чтобы избежать артефактов в тех областях конечного изображения, где один уровень mip-map структуры переходит в другой, обычно используют линейную интерполяцию между двумя соседними уровнями пирамиды (это не сильно увеличивает вычислительную сложность, ведь координаты точек на соседних уровнях однозначно связаны).
Однако mip-map никак не учитывает тот факт, что сжатие изображения может быть анизотропным (вытянутым вдоль какого-то направления). Частично эту проблему позволяет решить rip-map. Структура в которой независимо хранятся изображения сжатые в раз по горизонтали и
раз по вертикали. В этом случае, после определения коэффициентов сжатия по горизонтали и по вертикали в данной точке конечного изображения, производится интерполяция между результатами с 4, сжатых в нужное число раз, копий исходного изображения. Но и этот метод не идеален, ведь он не учитывает, что направление анизотропии отличаться от направлений, параллельных границам исходного изображения.
Частично эту проблему позволяет решить алгоритм FAST (Footprint Area Sampled Texturing) [3]. Он объединяет идеи mip-map-а и суперсэмплинга. Мы оцениваем степень сжатия исходя из оси наименьшей анизотропии и выбираем число отсчетов пропорционально отношению длин наименьшей оси к наибольшей.
Прежде чем сравнивать эти подходы по вычислительной сложности, оговоримся, что в целях ускорения подсчета обратного проективного преобразования, рационально сделать следующую замену:
где ,
— матрица обратного проективного преобразования. Так как
и
функции одного аргумента мы можем их пред-подсчитать за пропорциональное линейному размеру изображения время. Тогда для вычисления координат прообраза одной точки конечного изображения
, потребуется только 1 деление и 2 умножения. Аналогичный трюк можно провернуть с частными производными, которые используются для определения уровня в mip-map или rip-map структуре.
Теперь мы готовы сравнить результаты по вычислительной сложности.
Вычислительная математика копия 1
Интерполяция – частный случай аппроксимации, когда аппроксимирующая кривая проходит через все точки таблицы, то есть
Задача интерполяции ставится так:
Функция y = f ( x ) задана в виде таблицы
Рассмотрим другие способы решения этой задачи.
3.1 Интерполяция по Лагранжу
3.2 Интерполяция при постоянном шаге
Конечной разностью функции y= f (x) c шагом D x = h называют функцию D y=f (x+h)-f(x). Это первая конечная разность. Вторая конечная разность D 2 y = D ( D y )=[ f ( x +2 h )- f ( x + h )]-[ f ( x + h )- f ( x )]= f ( x +2 h )-2 f ( x + h )+ f ( x ) и т.д.
Предположим, что функция y = f (x) задана в виде таблицы из четырех точек. Построим для нее таблицу конечных разностей:
Предположим, что шаг в этой таблице – постоянный, то есть
Запишем полином, проходящий через все точки таблицы (а это будет полином степени не выше третьей), в следующем виде:
После подстановки в ( 3.5) значений ai i=0,1,2,3 и q1 окончательно получаем:
Если точка х * расположена ближе к концу таблицы, то удобнее пользоваться формулой второго интерполяционного полинома Ньютона:
Результаты применения формул (3.6) и (3.7) – одни и те же, если используются одни и те же узлы таблицы.
3.3 Обратная интерполяция
Функция y задана в виде таблицы
Задачу можно решить по крайней мере двумя различными способами.
1. а) Строим интерполяционный полином (как правило, ИПЛ) y=Ln( x )
в) Решаем уравнение y * =Ln(x) любым подходящим численным методом (например, методом деления отрезка пополам).
Из рисунка видно, что задача может иметь не единственное решение.
2. а) Строим интерполяционный полином x=Ln( y )
в) Подставляем в этот полином значение y * и получаем x * :
Как правило, решения задачи, полученные первым и вторым способом, будут различными.
3.4 Численное дифференцирование
Численное дифференцирование – это вычисление производных от функций, заданных в виде таблицы. Задача решается в два этапа. На первом этапе строится интерполяционный полином. На втором этапе находятся производные (первая, вторая и т.д.) от этого полинома.
Если шаг постоянный, то на первом этапе строят ИПН.
Найдем первую производную от этого полинома.
Если производную нужно вычислить в каком-либо узле таблицы (например, в точке х=х0), то формулы (3.9) и (3.10) упрощаются, так как q1=0.
Задача численного дифференцирования относится к числу некорректных задач. Это означает, что сколь угодно малые погрешности в исходных данных могут привести к большим погрешностям результата решения, поэтому к численному дифференцированию не следует прибегать без особой необходимости. По тем же причинам обычно не вычисляют производные старших порядков.
Пример. Функция задана в виде таблицы из четырех точек. Вычислить значение функции в точке х=-1 и значение первой и второй производной в этой же точке.
3.5 Численное интегрирование
Численное интегрирование – это вычисление определенных интегралов от функций, заданных либо в явном виде (например, Undetermined error: ), либо в виде таблицы. В любом случае функцию приводят к табличному виду, задавая шаг h и вычисляя значения подынтегральной функции в определенных точках. Интегралы вычисляют с помощью так называемых квадратурных формул, то есть
К численному интегрированию прибегают тогда, когда интеграл либо невозможно вычислить точными методами, либо это сделать сложно.
Для нахождения коэффициентов Ai в формуле (3.13) функцию y=f(x) заменяют интерполяционным полиномом. Интеграл от полинома легко вычисляется.
Для нахождения двойных определенных интегралов существуют соответствующие кубатурные формулы (с двойными суммами).
Существует множество квадратурных формул. Рассмотрим три из них.
1. Формулы прямоугольников
а) формула левых прямоугольников
в) формула правых прямоугольников
с) формула центральных прямоугольников
(3.16)
2. Формула трапеций
3. Формула Симпсона
1а. Обобщенная формула левых прямоугольников
1с. Обобщенная формула центральных прямоугольников
2а. Обобщенная формула трапеций
3а. Обобщенная формула Симпсона
Число точек в формуле Симпсона должно быть нечетным.
Каждую из формул нетрудно запрограммировать.
Вычислить Undetermined error: =[x-ln(1+x)]|0 4 =4-ln5 » 2.391
Взять шаг равным одной четвертой длины интервала интегрирования.
Интерполяция + (линейная | логарифмическая) шкала + С++
В этой статье я распишу теорию (а также базовые виртуальные классы), в следующей возьмусь за конкретные реализации средствами Qt.
Осторожно: в тексте много графики!
Откуда растут ноги у задачи
В общем, надо мне сделать регулятор холостого хода — такая штука для автомобиля, которая при холостом ходе в зависимости от температуры двигателя должна поддерживать определенные обороты. Поддерживает она их, регулируя заслонку шаговым двигателем.
В общем, мне надо знать текущую температуру. Было решено измерять ее штатными средствами — с терморезистора. Измеряем падение напряжения на нем — получаем сопротивление. Далее из таблицы (поскольку это микроконтроллер) получаем требуемые обороты.
Таблицу эту надо задать (для этого программа пишется средствами Qt). У меня есть несколько точек «сопротивление => температура». Мне надо для каждого кода АЦП (для ряда значений сорпотивлений) получить соответствующую температуру. Поскольку у разных автомобилей эти значения могут быть разными, то надо на экране, сверившись с таблицей, задать несколько точек на кривой.
По ходу дела оказалось, что график этот будет явно в логарифмическом масштабе. Значит, надо его вывести на экран. Как это сделать — читаем дальше.
Постановка задачи
Давайте немного подробнее опишем что нам надо:
Вот такое ТЗ… Ну да ничего, я справился! Давайте и вам помогу.
Да, пока не нырнули — спасибо Equation Editor-у от CodeCogs! С их помощью я лихо построил все математические формулы без всяких Microsoft Equation Editor, которые потом надо еще экспортировать в графику со вставкой сюда. Кстати, там есть и русский редактор. В общем, рекомендую!
Ну и если вместо формул вы видите пустые квадратики — это тоже «спасибо» Equation Editor-у…
Прикрепленный Excel-файл
По ходу написания статьи я все расчеты строил и проверял в таблице Excel с формулами. Оказалось очень удобно. И я решил его выложить для общественного пользования. Там внизу перечислены страницы по разделам. На каждой странице параметры, которые можно менять, отмечены как ячейки с желтым фоном. Остальные клетки лучше не трогать. Впрочем, все формулы можно смело смотреть. Скачивайте файлик и пробуйте на здоровье! Если проблемы с файлом — пишите, вышлю.
Функциональная зависимость
Итак, у нас есть некоторая зависимость — обозначим ее как 




Почему не 
только в школе в простейшем случае.


задает вертикальное смещение горизонтальной оси относительно нуля,
задает горизонтальное смещение вертикальной оси относительно нуля.

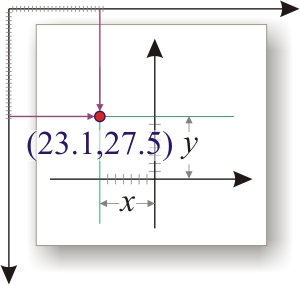
Ну и не забываем о том, что это все эти красивые рассуждения справедливы пока что для линейной шкалы, а у нас маячит за горизонтом логарифмическая. Там вообще черт знает что будет!
Но это только лишь точка. А у нас будет какая-то линия, точнее — много линий. Что там будут за преобразования?
Вот именно поэтому мы с самого начала должны четко разделить функциональную зависимость и преобразования координат.
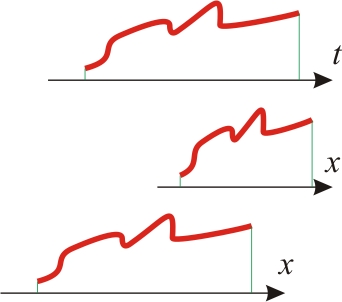
Итак, давайте договоримся о следующем: у нас есть некоторый абстрактный процесс, который описывается функциональной зависимостью 
, где
,
. Следующие шаги — это прояснить эти самые


Но отложим пока в сторону координаты — нам надо как-то задать нашу функцию (помните ТЗ)? Причем задать в тех самых абстрактных координатах 
Интерполяция
В моем случае был известен ряд точек 
 , Ω , Ω |  , ˚ , ˚ |
|---|---|
| 180 | 100 |
| 6 000 | 0 |
| 30 000 | -30 |




Многочлен вычисляется как 

Математика испугала? Хм… Ладно, напишу на языке С++:
Как видите, все достаточно тривиально (насколько тривиальными могут быть полиномы).
Еще одно большое достоинство полиномов Лагранжа — их легко можно промоделировать в таблице Excel-я, что я и делал.
Потом, правда, все стало немного печально, т. к. у этих полиномов, как и у любых других, на графике видны вибрации. Т. е. они не могут дать прямые линии — постоянные значения. В моем случае я не смог их настроить дОлжным образом — они выгибались в явно недопустимые числа. Поэтому мне пришлось от них отказаться…


Говоря языком математики, мы между точками и проводим прямые линии вида .
Опять же, на языке С++ это будет выглядеть так:
Тоже ничего революционного, не так ли?
Есть одно существенное различие между полиномом Лагранжа и линейной интерполяцией: у первого нельзя явно задать значения за пределами точек — они вычисляются, у второго можно это дело контролировать. Также и поэтому я в конечном итоге остановился на линейном варианте. Более того — в логарифмическом масштабе, к которому я стремился, линейные отрезки дают более подходящий мне вариант.
Впрочем, не будем заморачиваться сейчас на методах интерполяции. Давайте лучше мы сделаем базовый класс, от которого будем наследовать реализации различных методов $#*@!поляции.
Базовый класс для задания/расчета функции
Что этот класс должен уметь делать? Мне кажется, что такой класс должен:
Еще есть мысли? Если будут — пишите в комментариях, добавим!
Получается такой вот класс:
(Тем, кто недоволен моим стилем и структурой — предложите объективно лучше!)
(Тем, кто найдет ошибки в коде — спасибо!)
Думаю, тут все очевидно.
Для координат используется представление точки в виде QPointF (пара чисел в виде qreal, qreal. «На всех платформах, кроме ARM, используется double» — так написано для Qt 4.8).
В следующей статье мы распишем пару вариантов реализации этого класса.
Функция преобразования для вертикальной/горизонтальной шкалы
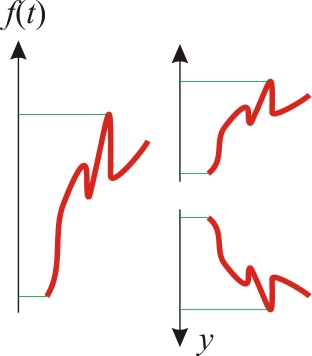
Есть линейные и логарифмические шкалы. Учитывая, что вертикальная шкала может быть сделана в одном формате, а горизонтальная — в другом, мы получаем четыре варианта графика:
Вариант первый — обе шкалы линейные. Вариант второй — обе логарифмические. Варианты третий и четвертый — смешанные графики. Кстати, в моем случае именно смешанный случай в итоге и подошел, т. к. по горизонтали у меня потребовался логарифмический масштаб, по вертикали — линейный.
Следовательно, задачу отображения нужно решать отдельно для обеих осей.
Напомним, что при отображении на экран используется преобразование в координаты , где
,
. Наша дальнейшая задача — построить эти функции для линейного и логарифмического случаев.
Что это за функции такие? На вход они получают координату в абстрактных (для компьютерной подпрограммы отображения на экран) координатах, на выход дают в экранных («экранные» координаты будут для разных операционных систем разными»). Для расчета им нужно знать следующее:
Базовый класс для преобразований шкал
Давайте сформулируем желаемую функциональность виртуального класса преобразований для шкалы, от которого будут унаследованы реализации шкал:
Реализация может выглядеть так:
Линейное преобразование
Давайте отдельно рассмотрим линейное преобразование для горизонтальной и вертикальной оси.
Расчет этих констант достаточно прост — это решение системы двух уравнений:
Еще важно уметь делать обратное преобразование — скажем, координаты указателя мыши перевести в абстрактные координаты. Также ничего сложного:
Шаг в данном случае для расчета не используется, но он потом нам пригодится в реализации на С++ для расчета смещения.
Как это будет использоваться на практике? Да все просто! Горизонтальное преобразование: — граница картинки графика, соответствующая (как правило, слева), — (как правило, справа), — шаг вывода картинки по горизонтали. Вертикальное преобразование — аналогично, но по вертикали (у нас в Qt будет нижней границей картинки, — верхней, причем scr_
Логарифмическое преобразование
А теперь окунемся туда, ради чего все это закрутилось:
(на графике не логарифм нарисован, а что-то похожее на него. Сделано это специально, т. к. логарифм тут будет не очень нагляден)
Вроде бы базовую математику рассмотрели. Нашли ошибки или неточности — пишите в комментариях, буду благодарен!
Со временем напишу следующую статью — реализацию этой математики средствами Qt языка C++.