что такое метод экстраполяции

Что такое экстраполяция простыми словами

Экстраполяция простыми словами — это способ сделать предположения о будущем или о некоторой гипотетической ситуации на основе данных, которые вам уже известны. Вы в основном делаете своё «лучшее предположение». Например, предположим, что ваша заработная плата увеличивается в среднем на две тысячи рублей в год. Можете экстраполировать и сказать, что через 10 лет ваша заработная плата должна быть примерно на двадцать тысяч рублей выше, чем сегодня.

Процесс, в котором вы оцениваете значение заданных данных за пределами их диапазона, называется методом экстраполяции.

Где применяется термин

Использование в реальной жизни

Вы до некоторой степени экстраполируете свою повседневную жизнь. Например, можете рассчитывать на ежемесячную зарплату и предполагать, что получите её на основе известных данных (того факта, что вам платили ежемесячно и вовремя за последний год). Но что, если ваша компания обанкротится? Или рынок рушится? Или банк по ошибке замораживает ваш банковский счёт? В этом конкретном случае экстраполяция имеет достаточную степень уверенности (вы, вероятно, получите свою заработную плату), но это не всегда так.

Использование в статистике

В статистике этот термин может означать несколько вещей, но все они связаны с предположениями (экстраполяция — это далеко не точная наука!):

Другое практическое использование

Также термин используется во многих областях науки, например, в химии и технике, где он часто бывает необходим. К примеру, если вам известны текущие напряжения конкретной системы, вы можете экстраполировать эти значения, чтобы предсказать, как система может реагировать на более высокие напряжения.

Способы экстраполяции

Линейный

Если хотите предсказать значение, которое не слишком далеко от существующих данных, линейная экстраполяция поможет вам для любой линейной функции. Когда вам предоставлен график, вы используете этот метод, чтобы провести касательную линию в последней точке и расширить эту линию за её пределы.

Конический

Этот тип помогает создать конический разрез с последними пятью конечными точками данных. Когда у вас есть пара или гипербола, кривая конического сечения расположена относительно оси х и не изгибается, но в случае эллипса или круга она изгибается сама по себе.

Полиномиальный

Можете создать полиномиальную кривую, используя все предоставленные вам точки данных. Этот метод применяется с использованием системы конечных рядов Ньютона или интерполяции Лагранжа. С помощью связанных точек вы можете найти необходимые данные.

Кто и когда придумал термин

Термин также носит название экстраполяцией Ричардсона или же методом Ромберга. Однако данные названия не совсем корректны, так как задолго до появления этих учёных уже были подобные численные способы решения аналогичных задач. По этой причине экстраполяция Ричардсона не считается первой. Похожий способ применялся в расчётах Гюйгенса ещё в 1654 году. Само понятие «экстраполяция» впервые ввёл Кларесон в 1959 году.

Источник

СОДЕРЖАНИЕ

Методы

Обоснованный выбор того, какой метод экстраполяции применить, зависит от предварительного знания процесса, в результате которого были созданы существующие точки данных. Некоторые эксперты предложили использовать причинные силы при оценке методов экстраполяции. Ключевыми вопросами являются, например, можно ли предположить, что данные являются непрерывными, гладкими, возможно периодическими и т. Д.

Линейный

Линейная экстраполяция означает создание касательной в конце известных данных и расширение ее за этот предел. Линейная экстраполяция даст хорошие результаты только при использовании для расширения графика приблизительно линейной функции или не слишком далеко за пределы известных данных.

Полиномиальный

Полиномиальная кривая может быть построена по всем известным данным или ближе к концу (две точки для линейной экстраполяции, три точки для квадратичной экстраполяции и т. Д.). Полученная кривая затем может быть расширена за пределы известных данных. Полиномиальная экстраполяция обычно выполняется с помощью интерполяции Лагранжа или с использованием метода конечных разностей Ньютона для создания ряда Ньютона, который соответствует данным. Полученный полином можно использовать для экстраполяции данных.

Коническая

Французская кривая

Геометрическая экстраполяция с предсказанием ошибок

Может быть создан с 3 точками последовательности и «моментом» или «индексом», этот тип экстраполяции дает 100% точность прогнозов в большом проценте базы данных известных серий (OEIS).

Пример экстраполяции с предсказанием ошибки:

m = последняя последовательность (5)

Качество

Как правило, качество конкретного метода экстраполяции ограничивается предположениями о функции, выполняемой этим методом. Если метод предполагает, что данные гладкие, то негладкая функция будет плохо экстраполирована.

Что касается сложных временных рядов, некоторые эксперты обнаружили, что экстраполяция более точна, если выполняется путем разложения причинных сил.

Взятие большего количества членов в степенной ряд sin ( x ) около x = 0 приведет к лучшему согласованию в большем интервале около x = 0, но приведет к экстраполяции, которая в конечном итоге отклонится от оси x даже быстрее, чем линейное приближение.

Это расхождение является специфическим свойством методов экстраполяции и обходится только тогда, когда функциональные формы, принимаемые методом экстраполяции (непреднамеренно или намеренно из-за дополнительной информации), точно отражают природу экстраполируемой функции. Для конкретных задач эта дополнительная информация может быть доступна, но в общем случае невозможно удовлетворить все возможные варианты поведения функций с работоспособным небольшим набором потенциального поведения.

В комплексной плоскости

Опять же, аналитическому продолжению могут помешать функциональные особенности, которые не были очевидны из исходных данных.

Быстрый

Экстраполированные данные часто свертываются в функцию ядра. После экстраполяции данных размер данных увеличивается в N раз, здесь N составляет примерно 2–3. Если эти данные необходимо преобразовать в известную функцию ядра, численные вычисления увеличатся в N log (N) раз даже при использовании быстрого преобразования Фурье (БПФ). Есть алгоритм, который аналитически рассчитывает вклад части экстраполированных данных. Время вычисления можно опустить по сравнению с исходным вычислением свертки. Следовательно, с этим алгоритмом вычисления свертки с использованием экстраполированных данных почти не увеличиваются. Это называется быстрой экстраполяцией. Быстрая экстраполяция была применена к реконструкции изображения КТ.

Аргументы экстраполяции

Подобно аргументам о скользкой дорожке, аргументы экстраполяции могут быть сильными или слабыми в зависимости от таких факторов, как то, насколько экстраполяция выходит за пределы известного диапазона.

Источник

Научная электронная библиотека

Громова Н. М., Громова Н. И.,

2.4 Методы прогнозной экстраполяции

При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта. Экстраполируются оценочные функциональные системные и структурные характеристики. Экстраполяционные методы являются одними из самых распространенных и наиболее разработанных среди всей совокупности методов прогно­зирования.

С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результа­тивности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др.

Однако степень реальности такого рода прогнозов и соответ­ственно мера доверия к ним в значительной мере обусловливаются аргументированностью выбора пределов экстраполяции и стабиль­ностью соответствия «измерителей» по отношению к сущности рас­сматриваемого явления. Следует обратить внимание на то, что слож­ные объекты, как правило, не могут быть охарактеризованы одним параметром. В связи с этим можно сделать некоторое представление о последовательности действий при статистическом анализе тенден­ций и экстраполировании, которое состоит в следующем:

— во-первых, должно быть четкое определение задачи, выдвиже­ние гипотез о возможном развитии прогнозируемого объекта, обсуж­дение факторов, стимулирующих и препятствующих развитию данного объекта, определение необходимой экстраполяции и её допустимой дальности;

— во-вторых, выбор системы параметров, унификация различных единиц измерения, относящихся к каждому параметру в отдельности;

— в-третьих, сбор и систематизация данных. Перед сведением их в соответствующие таблицы еще раз проверяется однородность дан­ных и их сопоставимость: одни данные относятся к серийным изде­лиям, а другие могут характеризовать лишь конструируемые объекты;

— в-четвертых, когда вышеперечисленные требования выполнены, задача состоит в том, чтобы в ходе статистического анализа и не­посредственной экстраполяции данных выявить тенденции или симп­томы изменения изучаемых величин. В экстраполяционных прогнозах особо важным является не столько предсказание конкретных значе­ний изучаемого объекта или параметра в таком-то году, сколько своевременное фиксирование объективно намечающихся сдвигов, ле­жащих в зародыше назревающих тенденций.

Для повышения точности экстраполяции используются различные приемы. Один из них состоит, например, в том, чтобы экстраполи­руемую часть общей кривой развития (тренда) корректировать с уче­том реального опыта развития отрасли-аналога исследований или объекта, опережающих в своем развитии прогнозируемый объект.

Под тенденцией развития понима­ют некоторое его общее направление, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории.

Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20-25 лет. Применяе­мый в прогнозировании метод экстраполяции не дает точных резуль­татов на длительный срок прогноза, потому что данный метод исхо­дит из прошлого и настоящего, и тем самым погрешность накапли­вается. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов не более 5 лет.

Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпиричес­ким значениям применяется метод наименьших квадратов. Его сущ­ность состоит в минимизации суммы квадратов отклонений меж­ду наблюдаемыми (фактическими) величинами и соответствующими оценками (расчет­ными величинами), вычисленными по подобранному уравнению связи.

Этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неуч­тенных.

Рассмотрим простейшие приемы экстраполяции. Операцию экстра­поляции в общем виде можно представить в виде определения значе­ния функции:

, (2.7)

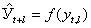
где 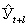— экстраполируемое значение уровня; L – период упреждения; У_t – уровень, принятый за базу экстраполяции.

Под периодом упреждения при прогнозировании понимается от­резок времени от момента, для которого имеются последние статис­тические данные об изучаемом объекте, до момента, к которому относится прогноз.

Экстраполяция на основе среднего значения временного ряда. В самом простом случае при предположении о том, что средний уровень ряда не имеет тенденции к изменению или если это изменение незначительно, можно принять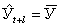т.е. прогнозируемый уровень равен среднему значению уровней в прошлом.

Доверительные границы для средней при небольшом числе на­блюдений определяются следующим образом:

(2.8)

(2.9)

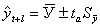
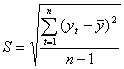
где y_t – фактические значения показателя.

Доверительный интервал, полученный как t_a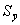, учитывает неопределенность, которая связана с оценкой средней величины.

Общая дисперсия, связанная как с колеблемостью выборочной средней, так и с варьированием ндивидуальных значений вокруг средней, составит величину S 2 +S 2 /n. Таким образом, доверительные интервалы для прогностической оценки равны:

(2.10)

Источник

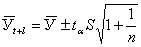
Метод экстраполяции

Добавлено в закладки: 0

М етод экстраполяции – это один из главных способов прогноза, который основывается на прогнозировании событий, учитывая анализ показателей, которые имели место в прошлые годы (при этом, не меньше чем за 5 – 8 лет). В данный момент есть приблизительно триста уравнений, которые дают возможность определить тенденции процессов и позволяют оценить линейную простую зависимость явления и квадратичную зависимость.

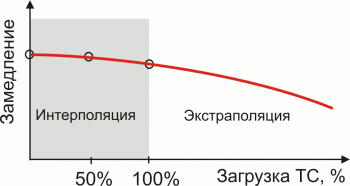
Экстраполи́рование, экстраполя́ция, (от лат. extrā — снаружи, вне, кроме, за и лат. polire — выправляю, приглаживаю, меняю, изменяю) — это особенный вид аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не меж фиксированными значениями.

Другими словами, экстраполяция — это приближённое определение значений функции в точках, которые лежат вне отрезка, по её значениям в точках.

Методы

Во многих случаях методы экстраполяции похожи с методами интерполяции.

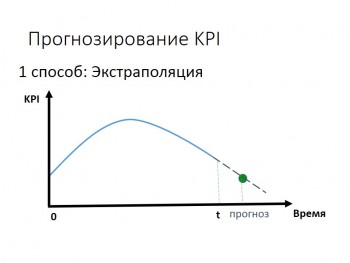
Самый распространённый способ экстраполяции — это параболическая экстраполяция, при которой в точке берётся значение многочлена степени, которая принимает в точке заданные значения. Для параболической экстраполяции применяют интерполяционные формулы.

Применение

Общее значение — это распространение выводов, которые получены из наблюдения над одной частью явления, на его другую часть.

В маркетинге — это распространение выявленных закономерностей развития изучаемого предмета на будущее.

В статистике — это распространение тенденций, установленных в прошлом, на будущий период (экстраполяция во времени используется для перспективных расчетов населения); распространение выборочных данных на прочую часть совокупности, которая не подвергнута наблюдению (экстраполяция в пространстве).

Одним из более распространенных способов краткосрочного прогнозирования экономических явлений — это экстраполяция

Термин “экстраполяция” имеет немного толкований в широком смысле экстраполяция – это способ научного исследования, который заключается в распространении выводов, которые получены из наблюдений за одной частью явления, на а другую его часть В узком смысле – это определение по нескольким данным функции прочих ее значений вне данного ряда за этим рядом.

Прогноз экстраполяции

Экстраполяция заключена в изучении сложившихся в настоящем и прошлом устойчивых тенденций экономического развития и их перенос на будущее

Цель данного прогноза — это показать, к каким итогам можно сделать в будущем, когда передвигаться к нему с аналогичной ускорением или скоростью, что и в прошлом

Прогноз определяет ожидаемые варианты данного экономического развития исходя из гипотезы, что главные факторы и тенденции прошлого периода сберегается на период прогноза или что возможно обосновать и учесть направление их изменений в рассматриваемой перспективе. Такую гипотезу выдвигают, учитывая инертность экономических процессов и явлений.

В прогнозировании экстраполяция используется при изучении временных рядов экстраполяции в общем типе можно представить, как определенное значение функции зависимо от особенностей изменения уровней в рядах динамики способы экстраполяции могут быть сложными и простыми.

Простые способы экстраполяции базируются на предположении относительной устойчивости в будущем абсолютных значений уровней, среднего абсолютного прироста, среднего уровня ряда, среднего темпа роста.

Различные способы экстраполяции

Рассмотрим дет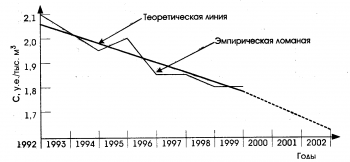альнее названные способы экстраполяции.

При экстраполяции на основании среднего уровня ряда применяется принцип, при котором прогнозируемый уровень равняется среднему значению в прошлом уровней ряда.

В данной ситуации экстраполяция дает точечную прогностическую оценку. Точное совпадение данных оценок с фактическими данными — маловероятное явление. Таким образом, прогноз обязан быть в виде интервала значений.

Полученный доверительный интервал учитывает неопределенность, которая связана с оценкой средней величины, и его использование для прогнозирования увеличивает степень надежности прогноза. Однако недостаток рассматриваемого подходов периода — это то, что доверительный интервал не связывается с периодом предупреждения.

Экстраполяцию по среднему абсолютному приросту можно провести тогда, когда линейной считать общую тенденцию развития явления.

Чтобы рассчитать прогнозное значение, уровень необходимо определить абсолютный средний прирост. Затем, зная уровень ряда динамики, который принимают за основу экстраполяции.

Экстраполяцию по среднему темпу роста можно осуществить, когда есть основания полагать, что суммарная тенденция ряда динамики характеризуется показательной кривой.

Доверительный интервал прогноза по средним темпом роста можно определить лишь в том случае, когда средний темп роста рассчитывают при помощи статистического оценивания параметров экспоненциальной кривой.

Все три рассмотренные способа экстраполяции тренда простейшие, но вместе и самые приближенные.

Сложные способы экстраполяции предусматривают выявление главной тенденции, то есть использование статистических формул, которые описывают тренд.

Способы данной группы возможно разделить на два главных вида: адаптивные и аналитические (кривые роста).

Аналитические способы прогнозирования

В основание аналитических способов прогнозирования (кривых роста) лежит принцип получения при помощи метода самых малых квадратов оценки детерминированной компоненты, которая характеризует главную тенденцию

Адаптивные способы прогнозирования основываются на том, что процесс реализации их заключен в вычислении последовательных во времени значений прогнозируемого показателя, учитывая степень влияния прошлых уровней. К ним относят способы экспоненциальной и текучей средних, способ гармонических весов, способ авторегрессииї.

Способ аналитического выравнивания тренда (способ наименьших квадратов) может быть использован лишь тогда, когда развитие явления довольно хорошо описывают построенную модель и условия, которые определяют тенденцию развития в прошлом, не изменятся существенно в будущем. При выполнении данных требований прогнозирование производится при помощи подстановки в уравнение тренда значений независимой переменной знает величине периода предупреждения.

Процедура создания прогноза по применению аналитического выравнивания тренда включает в себя такие этапы:

1) выбор формы кривой, которая отображает тенденцию;

2) определение показателей, характеризующие количественно тенденции изменений;

3) оценка вероятности прогнозных расчетов

Подбор формы кривой возможно осуществлять на основании построения графика, суммарный тип которого обычно дает возможность установить:

а) имеет динамический ряд показателя выраженную четко тенденцию;

б) если так, то данная тенденция плавная;

в) каков характер тенденции

Отвечая на данные вопросы, нужно помнить, что наружная простота графика ложная. Каждая динамическая задача намного сложнее от статического и каждая точка кривой — это результат изменения явления во времени и пространстве.

Ввиду этого для увеличения достоверности и обоснованности выравнивания для более точного выявления тенденции, которая есть, нужно провести вариантный расчет по некоторым аналитическими функциями и на основании статистических и экспертных оценок определить лучшую форму связей.

На втором этапе нужно определить параметры уравнения связи. Для того, чтобы их найти, применяют способ малых квадратов. В данной ситуации выравнивающая функция будет занимать данное положение среди факт политических значений показателей, при котором общее отклонение точек от функции будет наименьшим.

Обоснованную и достоверную оценку имеющимся результатам можно дать, применяя статистические показатели: средний коэффициент увеличения, коэффициент корреляции, остаточная и общая дисперсия, другой индекс корреляции, коэффициент корреляции ряда отклонений и исходного ряда, определенного по разнице выровненных и фактических по любой аналитической функции.

Для того, чтобы проверить гипотезу об отсутствии или наличии автокорреляции применяют таблицы с критическими значениями коэффициента автокорреляции при разных уровнях значимости. Когда табличное значение коефициэнта автокорреляции больше фактического, то возможно утверждать, что автокорреляция устраняется или отсутствует, а означает, возможно применять формулы для возиожностной оценки значений, которые прогнозируются по этому и точками.

Для прогноза были выбраны такие функции, как логарифмическая, линейная, ступенчатая, полиномиальная и экспоненциальная.

Не все выбранные аналитические функции выравнивают хорошо динамический выходной ряд. Об этом говорит значение индекса (коэффициента) корреляции Для того, чтобы прогнозировать, то есть продолжать сформированные тенденции на ближайшую перспективу, можно использовать лишь те функции, для которых индекс (коэффициент) корреляции больше 0,7 К таковым относят линейную, экспоненциальную и полиномиальную функцию. Последняя имеет самый большой коэффициент корреляции, равен 0,847, и самую малую величину остаточной дисперсией.

Порой, само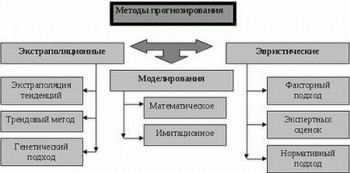й приемлемой формой аналитической функции для прогнозирования является полиномиальная функция, которая представлена уравнением:

Подставив в полученное уравнение значения периодов предубеждения, определяем прогнозное значение объема товарооборота на такие три месяца: у25 = 654,83; у = 655,93; у \”- 657,07 тыс грн 26 27

Возможность того, что экономический прогнозируемый показатель в заданный момент времени будет равняться значению, которое отвечает точечной прогноза, почти равняться нулю. Потому к точечному прогнозу границы вероятного изменения прогнозируемого значения показателя.

Заметим, что в полученных при прогнозировании оценок доверительных интервалов необходимо отнестись с осторожностью Это связывается со спецификой динамических рядов Их специфичность заключена в том, что увеличение количества наблюдений в статической совокупности дает возможность получить точные характеристики данной совокупности, в то время как аналогичное удлинение ряда динамики приводит не всегда к похожим результатам, особенно в тех ситуациях, когда ряды динамик применяются для прогнозирования. Данное обстоятельство связывается с тем, что информационная ценность уровней потеряется по мере их удаления от периода предубеждение, то есть означает уровни ряда динамики при прогнозировании неравноценно. Потому параметры уравнений аппроксимирующих кривых роста могут обладать погрешности и изменять собственные оценки при исключении части членов ряда или Анне добавил новых членов ряда динамики, что отображается на точности расчетных значений уровней ряда динамики. Помимо этого, параметры моделей тренда, которые получены способом самых малых квадратов, остаются неизменным и в течение рассматриваемого периода. На практике зачастую встречаются случаи, когда параметры моделей изменяются, а процедуры, которые сглаживают при помощи способа самых малых квадратов не могут определить такие изменения.

Поэтому наиболее эффективными являются адаптивные способы, в которых значимость уровней ряда динамики снижается по мере их удаления от прогнозируемого периода. К ним относят: способ текучих средних, способ экспоненциального сглаживания, способ гармонических весов и прочие, включаются в класс адаптивных способов.

Зачастую несколько динамики характеризуются резкими колебаниями показателей по годам. Данные ряды обычно, имеют слабую связь со временем и не проявляют четкой тенденции к изменению. В данной ситуации способы аналитического выравнивания малоэффективен, потому что возможность расчетов резко уменьшается. Доверительные границы прогноза порой оказываются шире, чем колебания показателя в некоторых динамиках.

При прогнозировании на основании временных рядов, которые весьма колеблются, можно применять способ текучих средних, при помощи которого возможно исключить случайные колебания временного ряда.

Интервал, величина которого все еще постоянная, постепенно помещается на одно наблюдение. Когда наблюдается определенная цикличность изменений показателей, интервал текучести равняется длительности циклу. В ситуации отсутствия цикличности в изменении показателей советуется исполнять различный расчет при параметре сглаживания. Лучший вариант определяется на основании дальнейшей оценки и выровненных рядов.

По данным выровненных значений ряда динамики производится подбор формы кривой, которая отражает тенденции развития явления. Полученное уравнение регрессии применяется для определения прогнозного значения исследуемого показатель.

На основании выровненных значений товарных запасов предприятия имеются такие значения коэффициента корреляции. Приведенные данные говорят, что наилучшие итоги должны по данным, которые выровнены на основании уровней исследуемого ряда динамики

Метод экспоненциального сглаживания

Экспоненциальное сглаживание – это выравнивание динамических рядов, весьма колеблются, цели стабильного прогнозирования По данному способу возможно дать обоснованные прогнозы на основе рядов динамики, имеют умеренный связь во времени, и обеспечить больше учета показателей, которые достигнуты за последние годы. Сущность метода оформляется в сглаживании временного ряда при помощи взвешенной текучей средней, в которые и веса подчиняются экспоненциальному закону.

Всякое сглажено значение рассчитано при помощи объединения прошлого текущего значения сглаженного значения и временного ряда. В данной ситуации текущие значения временного ряда разрешаются, учитывая константы, сглаживает.

Мы коротко рассмотрели м етод экстраполяции: методы, применение. Оставляйте свои комментарии или дополнения к материалу.

Источник