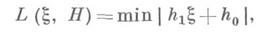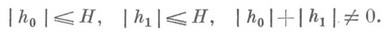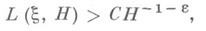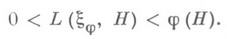что такое мера иррациональности
ИРРАЦИОНАЛЬНОСТИ МЕРА
где минимум берется по всевозможным парам h0, h1 целых рациональных чисел таких, что
Понятие И. м. является частным случаем понятий линейной независимости меры и трансцендентности меры. И. м. показывает, насколько «хорошо» может число x быть приближено рациональными дробями. Для всех действительных иррациональных чисел x выполняется неравенство
но при любом e>0 для почти всех (в смысле меры Лебега) действительных x
где С=С(e, x)>0. Однако для любой функции j(H)->0 при 

Лит.:[1] Xинчин А. Я., Цепные дроби, 3 изд., М. 1978.
Смотреть что такое «ИРРАЦИОНАЛЬНОСТИ МЕРА» в других словарях:
Открытые математические проблемы — Открытые (нерешённые) математические проблемы проблемы, которые рассматривались математиками, но до сих пор не решены. Часто имеют форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна… … Википедия
Пи (число) — У этого термина существуют и другие значения, см. Пи (значения). Иррациональные числа γ ζ(3) √2 √3 √5 φ α e π δ Система счисления Оценка числа … Википедия
e (число) — У этого термина существуют и другие значения, см. E. Не следует путать с Числами Эйлера I рода. Не следует путать с постоянной Эйлера. Иррациональные числа γ ζ(3) √2 √3 √5 φ α e π δ … Википедия
Трансцендентное число — (от лат. transcendere переходить, превосходить) это вещественное или комплексное число, не являющееся алгебраическим иными словами, число, которое не может быть корнем многочлена с целыми коэффициентами. Содержание 1 Свойства 2… … Википедия
ДИАЛЕКТИКА — (от греч. dialektike (techne) искусство вести беседу, спор) филос. теория, утверждающая внутреннюю противоречивость всего существующего и мыслимого и считающая эту противоречивость основным или даже единственным источником всякого движения и… … Философская энциклопедия
Непрерывная дробь — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия
Функция Минковского — Функция Минковского. Функция «вопросительный знак» Минковского построенная Германом Минковским монотонная с … Википедия
Подходящая дробь — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия
Подходящие дроби — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия
Число Лиувилля
Числа Лиувилля «почти рациональны» и поэтому могут быть «довольно точно» аппроксимированы последовательностями рациональных чисел. Это в точности те трансцендентные числа, которые можно более точно аппроксимировать рациональными числами, чем любое алгебраическое иррациональное число. В 1844 году Джозеф Лиувилль показал, что все числа Лиувилля трансцендентны, тем самым впервые установив существование трансцендентных чисел. [ необходима цитата ]
π и e не являются числами Лиувилля. [1]
Здесь мы показываем, что числа Лиувилля существуют, демонстрируя конструкцию, которая производит такие числа.
Из определения x следует, что его базовым b- представлением является
Теперь для любого целого n ≥ 1 определим q n и p n следующим образом:
Следовательно, мы заключаем, что любой такой x является числом Лиувилля.
Примечания к доказательству
Из этого следует заявленный вывод.
Теперь для любого целого n > 1 + log 2 ( d ) последнее неравенство выше влечет
Следовательно, число Лиувилля, если оно существует, не может быть рациональным.
Рассмотрим, например, число
Более того, числа Лиувилля образуют плотное подмножество множества действительных чисел.
Для натуральных чисел n > 2 и q ≥ 2 установите:
Заметим, что для каждого натурального числа n ≥ 2 и m ≥ 1 мы также имеем
Напротив, мера Лебега множества всех реальных трансцендентных чисел бесконечна (так как набор алгебраических чисел является нулевым множеством ).
Для каждого положительного целого числа n установите
Таким образом, множество всех чисел Лиувилля можно записать как
Практически все числа имеют показатель иррациональности, равный 2. [3] : 246
Ниже приводится таблица известных верхних и нижних оценок мер иррациональности некоторых чисел.
Примеры включают 1, 2 и 0,5
База иррациональности
Ниже мы покажем, что никакое число Лиувилля не может быть алгебраическим.
Поскольку α является корнем f, а p / q нет, мы видим, что | f ′ ( x 0 ) | > 0, и мы можем переставить:
что противоречит лемме. Следовательно, если число Лиувилля существует, оно не может быть алгебраическим и, следовательно, должно быть трансцендентным.
Однако обратите внимание, что π и e не являются числами Лиувилля.
СОДЕРЖАНИЕ
Существование чисел Лиувилля (постоянной Лиувилля)
Здесь мы показываем, что числа Лиувилля существуют, демонстрируя конструкцию, которая производит такие числа.
Теперь для любого целого n ≥ 1 определим q n и p n следующим образом:
Следовательно, мы заключаем, что любой такой x является числом Лиувилля.
Примечания к доказательству
Иррациональность
,> 
,> 
,>
.> 
> 
>
Если утверждение верно, то следует желаемый вывод.
.> 
,>
,>
>
Если, с другой стороны, с тех пор, поскольку является целым числом, мы можем утверждать более точное неравенство. Отсюда следует, что 0
\ влево | с \, qd \, р \ вправо |> 0
,> 
.>
Теперь для любого целого из последнего неравенства следует 1+\log _<2>(d)
,> 
.> 
\ влево | с \, qd \, р \ вправо |> 0
> 
>
,> 
,> 
,>
Следовательно, число Лиувилля, если оно существует, не может быть рациональным.
Бесчисленность
Рассмотрим, например, число
Более того, числа Лиувилля образуют плотное подмножество множества действительных чисел.
Числа Лиувилля и мера
Для натуральных чисел n > 2 и q ≥ 2 установите:
Заметим, что для каждого натурального числа n ≥ 2 и m ≥ 1 мы также имеем
Напротив, мера Лебега множества всех реальных трансцендентных чисел бесконечна (так как набор алгебраических чисел является нулевым множеством ).
Структура набора чисел Лиувилля.
Для каждого положительного целого числа n установите
U_ ^
\ left \
Таким образом, множество всех чисел Лиувилля можно записать как
\ bigcap \ limits _
.>
> 
>
Мера иррациональности
Практически все числа имеют показатель иррациональности, равный 2.
Ниже приводится таблица известных верхних и нижних оценок мер иррациональности некоторых чисел.
Примеры включают 1, 2 и 0,5
База иррациональности
Числа Лиувилля и трансцендентность
Ниже мы покажем, что никакое число Лиувилля не может быть алгебраическим.
Поскольку α является корнем f, а p / q нет, мы видим, что | f ′ ( x 0 ) | > 0, и мы можем переставить:
что противоречит лемме. Следовательно, если число Лиувилля существует, оно не может быть алгебраическим и, следовательно, должно быть трансцендентным.