что такое механическая система
iSopromat.ru
Под механической системой в механике понимается совокупность материальных точек (твердых тел), движения которых взаимосвязаны между собой.
Система материальных точек, движение которых не ограничено никакими связями, называется системой свободных материальных точек (примером являются планеты солнечной системы, движение которых по орбитам определяется действующими на них силами).
Определяющим признаком механической системы является наличие сил взаимодействия между отдельными материальными точками (телами) системы.
Действие связей на точки (элементы) механической системы выражается силами, называемыми реакциями связей. Поэтому все силы, действующие на систему несвободных точек, можно разделить на две группы: задаваемые (активные) силы и реакции связей. В то же время все силы, действующие на точки любой механической системы (свободной или несвободной), можно подразделить и по другому признаку: на внешние и внутренние силы.
Внешними называются силы, действующие на точки (тела) системы со стороны материальных точек (тел), не входящих в состав данной механической системы.
Внутренними называются силы взаимодействия между материальными точками (телами) данной механической системы.
Одна и та же сила может быть как внешней, так и внутренней, в зависимости от того, какая механическая система рассматривается. Так, например, реакции подшипников вала являются внешними силами относительно вала. Эти же реакции относятся к внутренним силам, когда рассматривается вся установка.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Набор студента для учёбы
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Механическая система. Силы внешние и внутренние
Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин».
Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.
Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.
Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.
Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.
В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.
Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.
Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.
Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.
Активными или задаваемыми силами называются все остальные силы, все кроме реакций.
Необходимость этой классификации сил выяснится в следующих главах.
Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.
Внутренние силы обладают следующими свойствами:
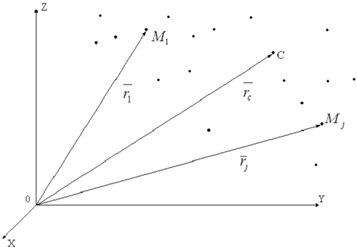
1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.31) действуют друг на друга с равными по модулю и противоположно направленными силами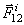 
и 
, сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то
Что такое механическая система
По поводу предмета механики уместно сослаться на слова авторитетного учёного-механика С. М. Тарга из введения к 4-му изданию его широко известного учебника теоретической механики: «Механикой в широком смысле этого слова называется наука, посвящённая решению любых задач, связанных с изучением движения или равновесия тех или иных материальных тел и происходящих при этом взаимодействий между телами. Теоретическая механика представляет собою часть механики, в которой изучаются общие законыдвижения и взаимодействия материальных тел, то есть те законы, которые, например, справедливы и для движения Земли вокруг Солнца, и для полёта ракеты или артиллерийского снаряда и т. п. Другую часть механики составляют различные общие и специальные технические дисциплины, посвящённые проектированию и расчёту всевозможных конкретных сооружений, двигателей, механизмов и машин или их частей (деталей)».
В приведённом высказывании упущен из виду тот факт, что изучением общих законов движения и взаимодействия материальных тел занимается также и механика сплошных сред (илимеханика сплошной среды) — обширная часть механики, посвящённая движению газообразных, жидких и твёрдых деформируемых тел. В этой связи академик Л. И. Седов отмечал: «В теоретической механике изучаются движения материальной точки, дискретных систем материальных точек и абсолютно твёрдого тела. В механике сплошной среды … рассматриваются движения таких материальных тел, которые заполняют пространство непрерывно, сплошным образом, и расстояния между точками которых во время движения меняются».
Таким образом, по предмету изучения механика подразделяется на:
Другой важнейший признак, используемый при подразделении механики на отдельные разделы, основан на тех представлениях о свойствах пространства, времени и материи, на которые опирается та или иная конкретная механическая теория. По данному признаку в рамках механики выделяют такие разделы:
Механическая система
Механика занимается изучением так называемых механических систем.
Механическая система обладает определённым числом 
степеней свободы, а её состояние описывается с помощью обобщённых координат 
и соответствующих им обобщённых импульсов 
. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.
Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.
Наиболее важными механическими системами являются:
Важнейшие механические дисциплины
| [показать] Фундаментальные понятия |
|---|
| [показать] Формулировки |
|---|
| [показать] Разделы |
|---|
| [показать] Учёные |
|---|
 Механика сплошных сред | |||||
 | |||||
| Сплошная среда | |||||
| |||||
| См. также: Портал:Физика |
| Квантовая механика | |||||||||
| |||||||||
| Принцип неопределённости | |||||||||
| Введение Математические основы | |||||||||
| |||||||||
| См. также: Портал:Физика |
Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся по содержанию) механические дисциплины:
Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.
Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).
Различные формулировки механики
Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, влагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.
Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.
Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.
Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.
Классическая механика
Границы применимости классической механики
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.
Что такое механическая система
Одним из основных понятий механики является понятие механической системы. Под механической системой понимают совокупность конечного или бесконечного числа материальных точек (или тел), взаимодействующих между собой в соответствии с третьим законом Ньютона. Отсюда следует, что движение каждой точки (или тела) системы зависит как от положения, так и от движения остальных точек рассматриваемой механической системы.
Системы различают свободные и несвободные. Система называется свободной, если все входящие в нее точки могут занимать произвольные положения и иметь произвольные скорости. В противном случае, т. е. когда материальные точки, входящие в систему, не могут занимать произвольных положений или же не могут иметь произвольных скоростей, система называется несвободной.
Примером свободной механической системы может служить солнечная система, в которой Солнце и планеты можно рассматривать как материальные тела, находящиеся под взаимным действием сил ньютонианского притяжения.
Примером несвободной системы может служить система, состоящая из 
точек, из которых одна или
несколько вынуждены при своем движении оставаться на каких-либо линиях или поверхностях.
С указанным делением систем на свободные и несвободные связано понятие связи.
Под связью в механике понимают условия, накладывающие ограничения на свободу перемещения точек системы. Связи могут накладывать ограничения как на положения точек, так и на их скорости. Практически связи осуществляются с помощью материальных тел или приспособлений (стержней, нитей, шарниров и т. п.).
Подобно тому как силы, действующие на точки системы, подразделяют на силы внутренние и силы внешние, так и связи, наложенные на точки системы, можно подразделить на связи внутренние и связи внешние. Под внутренними связями понимают такие связи, которые будучи наложены на точки системы, не препятствуют системе свободно перемещаться после того, как она внезапно отвердеет. Связь, не обладающая этим свойством, называется внешней. Например, если две точки твердого тела соединены между собой нерастяжимым и невесомым стержнем, то такая связь будет внутренней. Таким образом твердое тело можно рассматривать как систему, подчиненную внутренним связям. Если же одна из точек твердого тела шарнирно закреплена, то в этом случае связь будет внешней.
Система, подчиненная одним лишь внутренним связям, является свободной, так как она может перемещаться как свободное твердое тело. Если же в числе связей, наложенных на точки системы, имеются внешние связи, то система является несвободной.
Условия, ограничивающие свободу перемещения точек системы, аналитически выражаются в виде уравнений или неравенств вида.
где 
— время, 
— соответственно координаты и скорости 
точки системы,
отнесенные к некоторой инерциальной системе отсчета, относительно которой рассматривается движение данной системы.
Связи различают удерживающие и неудерживающие; первым соответствует знак равенства в (1.1), вторым — знак неравенства.
Удерживающие и неудерживающие связи иногда соответственно называют двухсторонними и односторонними связями. Удерживающая связь, препятствуя перемещению в одном направлении, препятствует также перемещению в противоположном направлении. Неудерживающая связь препятствует перемещению в одном направлении, но не препятствует перемещению в противоположном направлении.
Примером удерживающей связи могут служить две параллельные плоскости, между которыми происходит движение шарика. Рассматривая среднюю между ними плоскость как координатную плоскость 
получаем уравнение связи в виде: 
Если же шарик движется по горизонтальной плоскости 
любой момент может покинуть ее, то эта плоскость будет являться неудерживающей связью. Условие такой связи будет выражаться неравенством 
(или 
).
Другим примером неудерживающей связи может служить нить с шариком на конце. Принимая точку подвеса нити за начало координат и считая нить нерастяжимой, можем условие этой связи записать в виде неравенства
где 
— координаты шарика, 
— длина нити.
Если в процессе движения шарика выполняется неравенство
то это означает, что нить ослаблена и шарик освободился от связи.
Если же при движении шарика выполняется равенство
то это означает, что нить натянута, и на шарик действует связь.
В зависимости от того, содержит ли уравнение связи в явном виде время 
или нет, связи подразделяются на нестационарные (реономные) и стационарные (склерономные).
Связи, которые накладывают ограничения только на положения точек системы, называются конечными или геометрическими; аналитически они выражаются уравнением
Здесь и в дальнейшем предполагаем связи удерживающими.
Если же связи накладывают ограничения не только на положения точек, но и на их скорости, то они называются дифференциальными или кинематическими, и их аналитическое выражение имеет вид
Связи подразделяют также на голономные и неголономные. К голономным связям относят все конечные или геометрические связи вида (1.2), т. е. все связи, которые накладывают ограничения на возможные положения точек системы. К голономным связям относятся также и дифференциальные связи, которые путем интегрирования могут быть приведены к соотношениям вида (1.2):
где 
— некоторые функции координат 
возможно, времени 
.
Если же дифференциальные связи вида (1.4) не могут быть путем интегрирования приведены к конечным соотношениям вида (1.2), то они называются
неголономными или неинтегрируемими. Г. Герц обратил внимание на важность различия между голономными и неголономными связями для понятия виртуального перемещения системы.
Легко видеть, что если голономные связи накладывают ограничения на возможные положения точек системы, то неголономные связи накладывают ограничения на скорости точек системы. Это следует из того, что уравнение неголономной связи (1.4) всегда может быть представлено в следующем виде:
Механические системы, подчиненные голономным связям, называются голономными системами. Если же в числе связей имеются неголономные, то системы называются неголономными.
Если на систему наложены только неголономные связи, то такая система называется сдвершенно неголономной или собственно неголономной.
Классическим примером движения неголономной системы может служить качение твердого шара по шероховатой плоскости (например, движение бильярдного шара).
Пусть твердый шар радиусом 
катится без скольжения по абсолютно шероховатой плоскости. Возьмем две системы координат с общим началом в центре шара С. Одна из них (система пусть движется поступательно, а вторая (система 
) пусть будет жестко связана с шаром (рис. 1).
Положение шара в каждый момент времени может быть определено пятью координатами: двумя координатами центра шара 
(третья координата 
) и тремя углами Эйлера: углом прецессии 
углом нутации 0 и углом собственного вращения 
(рис. 1). Условием связи в рассматриваемой задаче является условие касания шара с плоскостью и обращение
в нуль скорости точки А касания шара. Принимая центр шара С за полюс и обозначая его скорость через 
мгновенную угловую скорость вращения шара — через 
, а вектор-радиус, проведенный из центра шара в точку касания 
, — через 
, можем записать скорость точки А в следующем виде:
Проектируя это векторное равенство на оси координат и удовлетворяя условию связи 
получаем
где 
— составляющие вектора угловой скорости 
. Последнее уравнение интегрируется и дает одно уравнение связи 
показывающее, что центр шара С движется в плоскости, параллельной плоскости 
и отстоящей от нее на расстоянии, равном радиусу шара R.
Проекции угловой скорости на неподвижные оси выражаются, как известно, следующими формулами:
С помощью этих формул первые два уравнения связи (1.6) можно представить в следующем виде:
Эти два дифференциальных уравнения не могут быть приведены к конечным соотношениям путем интегрирования, и, следовательно, мы имеем здесь пример неголономной связи.
Посмотрим теперь, какой вид примут найденные уравнения связи (1.6) или, в развернутом виде, уравнения (1.8) в том случае, когда плоскость, по которой движется шар, будет абсолютно гладкая.
Рассматривая случай чистого скольжения, можем написать, что 
, следовательно,
Замечая, что 
получаем
Для интегрирования возведем оба уравнения в квадрат и сложим; тогда получим
Из этого соотношения следует
После интегрирования получаем
В рассматриваемом случае условие связи выражается равенством 
или 
т.е. связь голономна, и, следовательно, шар на абсолютно гладкой плоскости представляет собой пример голономной системы.
Примером неголономной связи может служить также случай качения и верчения диска с острыми краями по абсолютно шероховатой плоскости. Интересно отметить, однако, что плоскопараллельное движение диска — качение его по абсолютно шероховатой плоскости — дает пример голономной связи.
Действительно, в этом случае (рис. 2) условие связи имеет следующий вид:
Интегрируя, находим уравнения связи
а это означает, что связь будет голономной.
Из этого примера следует, что качение без скольжения цилиндра по абсолютно шероховатой плоскости также представляет случай голономной связи.