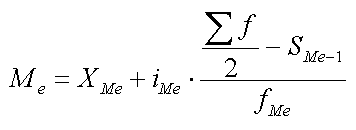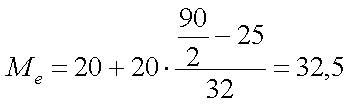что такое медиана набора чисел

Медиана (статистика)

Из Википедии — свободной энциклопедии

Медиа́на (от лат. mediāna «середина») набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше. Другое равносильное определение [1] : медиана набора чисел — это число, сумма расстояний (или, если более строго, модулей) от которого до всех чисел из набора минимальна. Это определение естественным образом обобщается на многомерные наборы данных и называется 1-медианой.

Например, медианой набора <11, 9, 3, 5, 5>является число 5, так как оно стоит в середине этого набора после его упорядочивания: <3, 5, 5, 9, 11>. Если в выборке чётное число элементов, медиана может быть не определена однозначно: тогда для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора <1, 3, 5, 7>принимают равной 4), подробнее см. ниже. В математической статистике медиана может использоваться как одна из характеристик выборки или совокупности чисел.

Также определяется медиана случайной величины: в этом случае оно определяется как число, которое делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2), — более точное определение дано ниже.

Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.

Источник

Золотая середина. Поиск медианного элемента потока входных чисел

В этой статье мы рассмотрим следующую задачу: поиск и поддержание медианы среди целых чисел, которые последовательно попадают на обработку. В этом посте мы поставим задачу, разберём все необходимые вводные, предложим и оценим сложность решения.

Постановка задачи

На вход алгоритму подаётся поток целых чисел, т.е. количество чисел может быть неизвестно, но мы будем считать, что массив задан наперёд и его длина очень большая. Требуется разработать алгоритм, который определяет медиану текущего массива, т.е. считанного из исходного к данному моменту. При этом требуется, чтобы сложность такого алгоритма была

Медиана ряда чисел

Либо можно выбирать элемент под номером , если чётное и если нечетное.

Наивный подход

Давайте обсудим бейзлайновое решение, при котором медиану можно получить за .

Пусть каждое новое число из потока мы будем вставлять в массив так, чтобы массив оставался упорядоченным. Затем будем выбирать элемент из середины и добавлять его в список медиан.

Как упоминалось выше, этот алгоритм будет иметь квадратичную сложность, поскольку для каждого из элементов потока, мы выполняем линейную работу по поиску места и вставке элемента в массив.

Улучшить этот результат нам поможет структура данных — куча.

Куча. Min-heap, max-heap

Рассмотрим кучу на примере min-heap. Min-heap — это бинарное дерево, обладающее двумя следующими свойствами:

Аналогично образом задаётся max-heap, нужно заменить «меньше» на «больше» в первом свойстве.
При решении задачи мы хотим воспользоваться операциями, которые благодаря построению кучи, могут быть выполнены быстрее, чем за линейное время.

Первая из этих операций: взятие минимума (максимума) и удаление

Работая с кучей, операцию взятия минимума можно осуществить за константное время. Поскольку минимум всегда хранится в корне дерева, то узнать его значение не составляет труда. Если же мы хотим удалить минимум и назначить на его место следующий по величине элемент, то нам потребуется вызвать метод extract, чья временная сложность тоже меньше линейной и равна .

Метод extract внутри себя запускает следующий процесс: сначала элемент с самого последнего уровня ставится в корень дерева, затем на корне дерева стартует метод bubble_down, который уровень за уровнем (а таких всего в полном дереве) опускает новый корневой узел.
Код реализации на языке Python смотри ниже.

Вторая операция: добавление элемента

Чтобы добавить произвольный элемент в кучу требуется выставить новый элемент на правильное место, не утратив 2 свойства кучи. Для этого новый элемент добавляется на последний уровень, а затем методом bubble_up поднимается в сторону корня, пока над ним не окажется элемент меньший него или он не станет корнем. Сложность этой операции также равна

Код, в котором мы определим необходимую функциональность с возможностью определения min и max-heap:

Оптимальное решение

Теперь перейдем непосредственно к реализации алгоритма контроля медианы, основанном на использовании кучи. Мы будем использовать две кучи, одну минимальную, другую максимальную. Идея заключается в следующем: давайте разделим поток значений на верхнюю часть, содержащую большие значения и нижнюю, содержащую меньшие значения. Первую реализуем на основе min-heap, чтобы легко получать минимальный элемент, который лежит на разделе, а вторую на основе max-heap.

Всякий раз, когда мы читаем из потока очередное число, будем добавлять его в верхнюю часть, если оно больше наименьшего из этой половины и в нижнюю часть, если верно обратное. Затем, осуществив вставку, будем балансировать две части, чтобы они содержали по половине из введенных значений.

Каждую итерацию внешнего цикла, мы делаем несколько шагов сложностью , посколько операции вставки и получения элемента из кучи ограничены этой сложностью. По этой причине итоговая сложность не превышает .

Заключение

В этой статье на примере задачи мы обсудили преимущества кучи по сравнению со списком. Познакомились с временной сложностью операций над этой структурой данных. Реализовали код этой структуры, необходимый для эффективного выполнения задачи по поиску медианного элемента в потоке чисел.

В преддверии старта курса «Алгоритмы и структуры данных» приглашаем всех желающих на бесплатный двухдневный интенсив по теме: Алгоритм сжатия данных — код Хаффмана.

Источник

Медиана

В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.

Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.

Понятие медианы

Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.

То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.

Формула для расчета медианы

Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.

Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.

Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:

X_me — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);

i_me — величина медианного интервала;

f — частота (сколько раз в ряду встречается то или иное значение);

S_me-1 — сумма частот интервалов предшествующих медианному интервалу;

f_me — число значений в медианном интервале (его частота).

Пример вычисления медианы

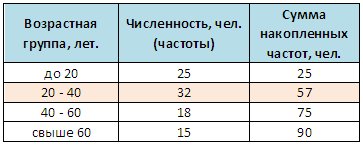
Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.

Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).

Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.

Область применения медианы

При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.

Особенности медианы

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Источник

Медиана ряда чисел

Понятие медианы чисел широко используется в математической статистике. И хотя вычисление медианы не составляет большой сложности, мы сделали калькулятор, который поможет рассчитать медианное значение ряда чисел онлайн с подробным решением. Причем количество чисел не важно, он рассчитает медиану 3, 4, 5 чисел так же быстро, как и для 1000 чисел.

Калькулятор медиана чисел

Как найти медиану чисел

Лучше рассмотреть процесс вычисления медианы на примере. Пусть у нас есть ряд чисел: 13 19 24 17 15 11. Для удобства числа будет записывать через пробел. Найдем его медиану. Для начала необходимо расположить числа в порядке возрастания. Эта процедура называется сортировкой. Получим новый ряд: 11 13 15 17 19 24. Так как количество чисел в ряду равно 6, а число 6 четное, то середина ряда будет между числами 15 и 17. Найдем среднее этих двух чисел: (15 + 17) / 2 = 16. Это и будет медианой ряда. Не стоит путать медиану, среднее гармоническое и среднее арифметическое — это принципиально разные понятия.

Рассмотрим другой пример, когда количество чисел в ряду нечетное. Есть такой ряд: 18 46 10 5 38. Найдем медиану набора этих чисел. Отсортируем ряд по возрастанию и получим ряд: 5 10 18 38 48. Так как количество чисел в этом ряду 5, то у него есть середина — это элемент с номером 2. Значит медиана этого ряда равна элементу с номером 2. Получаем ответ 18.

И еще пример — найдем медиану чисел 158 166 134 130 132. Отсортируем и получим ряд 130 132 134 158 166. Количество чисел нечетное и равно 5, значит средний элемент имеет номер 3. Третий элемент нашего отсортированного ряда — число 134. Это и есть медиана.

Источник

Медиана (статистика)

Также медиану можно определить для случайных величин: в этом случае она делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2); более точное определение см. ниже.

Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.

Связанные понятия

Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.

Упоминания в литературе

Связанные понятия (продолжение)

Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых.

Источник