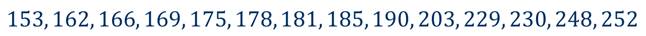что такое медиана числового ряда в математике

Золотая середина. Поиск медианного элемента потока входных чисел

В этой статье мы рассмотрим следующую задачу: поиск и поддержание медианы среди целых чисел, которые последовательно попадают на обработку. В этом посте мы поставим задачу, разберём все необходимые вводные, предложим и оценим сложность решения.

Постановка задачи

На вход алгоритму подаётся поток целых чисел, т.е. количество чисел может быть неизвестно, но мы будем считать, что массив задан наперёд и его длина очень большая. Требуется разработать алгоритм, который определяет медиану текущего массива, т.е. считанного из исходного к данному моменту. При этом требуется, чтобы сложность такого алгоритма была

Медиана ряда чисел

Либо можно выбирать элемент под номером , если чётное и если нечетное.

Наивный подход

Давайте обсудим бейзлайновое решение, при котором медиану можно получить за .

Пусть каждое новое число из потока мы будем вставлять в массив так, чтобы массив оставался упорядоченным. Затем будем выбирать элемент из середины и добавлять его в список медиан.

Как упоминалось выше, этот алгоритм будет иметь квадратичную сложность, поскольку для каждого из элементов потока, мы выполняем линейную работу по поиску места и вставке элемента в массив.

Улучшить этот результат нам поможет структура данных — куча.

Куча. Min-heap, max-heap

Рассмотрим кучу на примере min-heap. Min-heap — это бинарное дерево, обладающее двумя следующими свойствами:

Аналогично образом задаётся max-heap, нужно заменить «меньше» на «больше» в первом свойстве.
При решении задачи мы хотим воспользоваться операциями, которые благодаря построению кучи, могут быть выполнены быстрее, чем за линейное время.

Первая из этих операций: взятие минимума (максимума) и удаление

Работая с кучей, операцию взятия минимума можно осуществить за константное время. Поскольку минимум всегда хранится в корне дерева, то узнать его значение не составляет труда. Если же мы хотим удалить минимум и назначить на его место следующий по величине элемент, то нам потребуется вызвать метод extract, чья временная сложность тоже меньше линейной и равна .

Метод extract внутри себя запускает следующий процесс: сначала элемент с самого последнего уровня ставится в корень дерева, затем на корне дерева стартует метод bubble_down, который уровень за уровнем (а таких всего в полном дереве) опускает новый корневой узел.
Код реализации на языке Python смотри ниже.

Вторая операция: добавление элемента

Чтобы добавить произвольный элемент в кучу требуется выставить новый элемент на правильное место, не утратив 2 свойства кучи. Для этого новый элемент добавляется на последний уровень, а затем методом bubble_up поднимается в сторону корня, пока над ним не окажется элемент меньший него или он не станет корнем. Сложность этой операции также равна

Код, в котором мы определим необходимую функциональность с возможностью определения min и max-heap:

Оптимальное решение

Теперь перейдем непосредственно к реализации алгоритма контроля медианы, основанном на использовании кучи. Мы будем использовать две кучи, одну минимальную, другую максимальную. Идея заключается в следующем: давайте разделим поток значений на верхнюю часть, содержащую большие значения и нижнюю, содержащую меньшие значения. Первую реализуем на основе min-heap, чтобы легко получать минимальный элемент, который лежит на разделе, а вторую на основе max-heap.

Всякий раз, когда мы читаем из потока очередное число, будем добавлять его в верхнюю часть, если оно больше наименьшего из этой половины и в нижнюю часть, если верно обратное. Затем, осуществив вставку, будем балансировать две части, чтобы они содержали по половине из введенных значений.

Каждую итерацию внешнего цикла, мы делаем несколько шагов сложностью , посколько операции вставки и получения элемента из кучи ограничены этой сложностью. По этой причине итоговая сложность не превышает .

Заключение

В этой статье на примере задачи мы обсудили преимущества кучи по сравнению со списком. Познакомились с временной сложностью операций над этой структурой данных. Реализовали код этой структуры, необходимый для эффективного выполнения задачи по поиску медианного элемента в потоке чисел.

В преддверии старта курса «Алгоритмы и структуры данных» приглашаем всех желающих на бесплатный двухдневный интенсив по теме: Алгоритм сжатия данных — код Хаффмана.

Источник

Что такое медиана набора чисел

Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.

Среднее арифметическое, размах, мода и медиана

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Для ряда a₁,a₁. a_n среднее арифметическое вычисляется по формуле:

Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32

Модой ряда чисел называется число, которое встречается в данном ряду чаще других.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.

Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.

Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.

Примеры

Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.

Медиа́на (от лат. mediāna — середина) в математической статистике — число, характеризующее выборку (например, набор чисел). Если все элементы выборки различны, то медиана — это такое число выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него. В более общем случае медиану можно найти, упорядочив элементы выборки по возрастанию или убыванию и взяв средний элемент. Например, выборка после упорядочивания превращается в и её медианой является число 5. Если в выборке чётное число элементов, медиана может быть не определена однозначно: для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора принимают равной 4), подробнее см. ниже.

Также медиану можно определить для случайных величин: в этом случае она делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2); более точное определение см. ниже.

Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.

Содержание

Свойства медианы для случайных величин [ править | править код ]

Если распределение непрерывно, то медиана является одним из решений уравнения

F ( x ) = 0.5

Если распределение является непрерывной строго возрастающей функцией, то решение уравнения однозначно. Если распределение имеет разрывы, то медиана может совпадать с минимальным или максимальным (крайним) возможным значением случайной величины, что противоречит «геометрическому» пониманию этого термина.

Медиана является важной характеристикой распределения случайной величины и, так же как математическое ожидание, может быть использована для центрирования распределения. Поскольку оценки медианы более робастны, её оценивание может быть более предпочтительным для распределений с т. н. тяжёлыми хвостами. Однако о преимуществах оценивания медианы по сравнению с математическим ожиданием можно говорить только в случае, если эти характеристики у распределения совпадают, в частности, для симметричных функций плотности распределения вероятностей.

Медиана определяется для всех распределений, а в случае неоднозначности, естественным образом доопределяется, в то время как математическое ожидание может быть не определено (например, у распределения Коши).

Пример использования [ править | править код ]

Предположим, что в одной комнате оказалось 19 бедняков и один миллионер. У каждого бедняка есть 5 ₽, а у миллионера — 1 млн ₽ (10 6 ). В сумме получается 1 000 095 ₽. Если мы разделим деньги равными долями на 20 человек, то получим 50 004,75 ₽. Это будет среднее арифметическое значение суммы денег, которая была у всех 20 человек в этой комнате.

Медиана в этом случае будет равна 5 ₽ (полусумма десятого и одиннадцатого, срединных значений ранжированного ряда). Можно интерпретировать это следующим образом. Разделив всю компанию на две равные группы по 10 человек, мы можем утверждать, что в первой группе у каждого не больше 5 ₽, во второй же не меньше 5 ₽. В общем случае можно сказать, что медиана это то, сколько принёс с собой «средний» человек. Наоборот, среднее арифметическое — неподходящая характеристика, так как оно значительно превышает сумму наличных, имеющуюся у среднего человека.

Неуникальность значения [ править | править код ]

Здравствуйте!
Помогите разобраться с вопросом как найти медиану ряда чисел. Что такое медиана ряда чисел вообще?
Спасибо!

Как найти медиану ряда чисел
Во-первых, нахождение медианы ряда чисел отличается для четных и нечетных количеств элементов в ряду. Это следует из определения медианы.
Медиана ряда чисел – это число, которое стоит строго посередине ряда нечётного количества чисел, упорядоченного от наименьшего к наибольшему.
Для четного количества чисел в ряду медианой является половина суммы двух чисел, которые стоят посередине ряда, упорядоченного по возрастанию.
Рассмотрим примеры.

Пример 1.
Найдем медиану следующего ряда:
123, 78, 11, 95, 34, 67, 101, 356, 44, 73, 47.

Решение.
Сначала нужно записать числа этого ряда по возрастанию:
11, 34, 44, 47, 67, 73, 78, 95, 101, 123, 356.
Количество чисел в этом ряду равно 11, то есть оно нечетное. Поэтому медианой будет число, которое стоит посередине этого ряда. Это число 73.

Ответ. Медиана равна 73.

Пример 2.
Найдем медиану ряда:
23, 76, 34, 115, 6, 58, 88, 39, 17, 25, 7, 54, 49, 52.

Решение.
Сначала запишем числа данного ряда по возрастанию:
6, 7, 17, 23, 25, 34, 39, 49, 52, 54, 58, 76, 88, 115.
Количество чисел в этом ряду равно 14, то есть оно четное. Поэтому медианой будет половина суммы двух чисел, которые стоят посередине этого ряда. То есть (39 + 49) : 2 = 44.

Источник

Среднее арифметическое чисел. Мода. Медиана. Размах ряда чисел

Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.

Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.

Например: найдем среднее арифметическое чисел 2; 6; 9; 15.

У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.

Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.

Например: найдем размах чисел 2; 5; 8; 12; 33.

Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.

Мода ряда чисел – это число, которое встречается в данном ряду чаще других.

Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.

Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.

Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.

Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.

В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.

Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?

Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите медиану и размах ряда.

Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите моду ряда и среднее арифметическое ряда.

Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.

Найдите среднюю заработную плату.

Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.

Найдите разность среднего арифметического и медианы этого набора.

Найдите объем и медиану числового ряда.

Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:

Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.

Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.

Найдите среднее арифметическое этого набора чисел.

Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.

Найдите медиану этого набора чисел.

Провели несколько измерений случайной величины:

800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.

Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.

Найдите разность среднего арифметического и медианы этого набора.

Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.

Найдите среднее арифметическое, размах и моду.

Источник

Медиана как статистическая характеристика

Урок 11. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Медиана как статистическая характеристика»

· ввести понятие «медиана числового ряда».

На предыдущем уроке мы с вами познакомились с тремя статистическими характеристиками.

На этом уроке мы познакомимся с ещё одной статистической характеристикой.

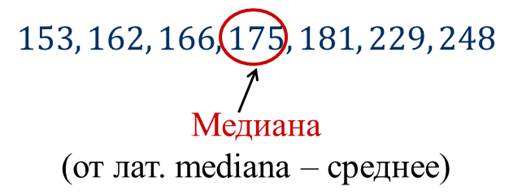
Давайте рассмотрим таблицу, в которой показано число посетителей музея в разные дни недели.

Составим из данных, приведённых в таблице, упорядоченный ряд.

В этом ряду семь чисел. Посмотрите, что в середине ряда расположено число 175: слева от него расположены 3 числа и справа тоже 3 числа. Число 175 называют срединным числом, или медианой упорядоченного ряда.

Слово «медиана» произошло от латинского слова «медиана», которое означает «среднее».

Число 175 считают и медианой исходного (неупорядоченного) ряда.

Теперь рассмотрим таблицу, в которой показано число посетителей музея в разные дни в течение двух недель.

Снова составим из приведённых данных упорядоченный ряд.

Обратите внимание, что в этом ряду чётное количество чисел, и поэтому мы не можем выбрать одно число, расположенное в середине и выберем два – 181 и 185.

Найдём среднее арифметическое этих чисел, то есть их сумму разделим на 2, и получим 183. Число 183 разбивает наш ряд на две равные по численности группы (слева от него находятся 7 чисел ряда и справа – 7 чисел ряда) и является медианой упорядоченного ряда и исходного. При этом обратим внимание, что само число 183 не является членом ряда.

В каждом из рассмотренных примеров, найдя медиану ряда, мы можем указать дни, когда количество посетителей музея превосходит срединное значение, то есть медиану, или, наоборот, меньше этого значения.

Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине.

А медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, расположенных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Источник

Медиана ряда чисел

Понятие медианы чисел широко используется в математической статистике. И хотя вычисление медианы не составляет большой сложности, мы сделали калькулятор, который поможет рассчитать медианное значение ряда чисел онлайн с подробным решением. Причем количество чисел не важно, он рассчитает медиану 3, 4, 5 чисел так же быстро, как и для 1000 чисел.

Калькулятор медиана чисел

Как найти медиану чисел

Лучше рассмотреть процесс вычисления медианы на примере. Пусть у нас есть ряд чисел: 13 19 24 17 15 11. Для удобства числа будет записывать через пробел. Найдем его медиану. Для начала необходимо расположить числа в порядке возрастания. Эта процедура называется сортировкой. Получим новый ряд: 11 13 15 17 19 24. Так как количество чисел в ряду равно 6, а число 6 четное, то середина ряда будет между числами 15 и 17. Найдем среднее этих двух чисел: (15 + 17) / 2 = 16. Это и будет медианой ряда. Не стоит путать медиану, среднее гармоническое и среднее арифметическое — это принципиально разные понятия.

Рассмотрим другой пример, когда количество чисел в ряду нечетное. Есть такой ряд: 18 46 10 5 38. Найдем медиану набора этих чисел. Отсортируем ряд по возрастанию и получим ряд: 5 10 18 38 48. Так как количество чисел в этом ряду 5, то у него есть середина — это элемент с номером 2. Значит медиана этого ряда равна элементу с номером 2. Получаем ответ 18.

И еще пример — найдем медиану чисел 158 166 134 130 132. Отсортируем и получим ряд 130 132 134 158 166. Количество чисел нечетное и равно 5, значит средний элемент имеет номер 3. Третий элемент нашего отсортированного ряда — число 134. Это и есть медиана.

Источник