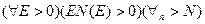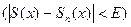что такое мажорирующий ряд

Мажорируемость функционального ряда

Определение 6.2.6. Функциональный ряд называется мажорируемым на данном множестве Д (на котором определены функции , где ), если существует такой числовой сходящийся ряд с положительными членами, что члены ряда (хотя бы начиная с некоторого) при всех не превосходят по модулю соответствующих членов ряда , т. е.

(При этом ряд называется мажорирующим или мажорантным рядом для функционального ряда).

! Другое определение6.2.7.Функциональный ряд (1) называется мажорируемым на данном множестве Д (на котором определены функции , где ), если существует такой сходящийся числовой ряд (2) с положительными членами, что для всех выполняются соотношения

,( )

Равномерная сходимость функционального ряда

Среди сходящихся функциональных рядов выделяются своей важностью так называемые равномерно сходящиеся ряды.

Определение 6.2.8. Ряд (1) называется равномерно сходящимся на множестве Д, если для любого можно указать такое число , что при всех будет выполнятся неравенство: для всех (или ).

— n-я частичная сумма ряда (1)

Рассмотрим следующий признак, достаточный для равномерной сходимости функционального ряда.

Теорема (признак Вейерштрасса) 6.2.15.: Если функциональный ряд (1) мажорирует на данном множестве Д, то он: 1) равномерно и 2) абсолютно сходится на этом множестве.

Пример 6.2.26.Доказать, что ряд сходится равномерно на всей оси ОХ.

Т. к. для » имеем , то ( ). Ряд сходится. По признаку Вейерштрасса данный ряд сходится равномерно на всей оси.

Замечание 6.2.8.Признак Вейерштрасса дает только достаточное условие равномерной сходимости функционального ряда, оно не является необходимым.

Замечание 6.2.9. Равномерно сходящийся в некотором промежутке ряд не обязательно сходится там и абсолютно.

Степенные ряды

Одним из важных классов функциональных рядов являются степенные ряды.

Определение 6.2.9.Функциональные ряды, членами которых являются целые положительные степени независимой переменной х или двучлена (х-х₀), ( где х₀=const), умноженные на числовые коэффициенты:

(1) , или

(2) называются степенными рядами.

Члены степенных рядов являются: 1) непрерывными и 2) дифференцируемыми функциями на всей числовой оси.

Ряд (1) получается из ряда (2) при х₀=0.

Все последующие рассуждения будем проводить для ряда (1), поскольку ряд (2) приводится к ряду (1) с помощью замены переменной х-х₀=Х.

Замечание 6.2.10. Для удобства n-м членом степенного ряда называют член , несмотря на то, что он стоит на (n+1)-м месте. Свободный член ряда a₀ считают нулевым членом.

Логически могут представиться 3 возможности:

1)ряд (1) сходится на свей числовой оси;

2)ряд сходится только в т. х=0 (в т. х=0 сходится всякий степенной ряд (1),

3) ряд сходится не только в точке х=0, но и не на всей числовой оси.

Источник

Свойства равномерно сходящегося ряда

Основные вопросы.

1. Функциональные ряды, основные понятия и свойства.

2. Степенные ряды. Теорема Абеля.

Краткое содержание

1. Функциональные ряды, основные понятия и свойства.

Пусть последовательность функций, определенных в некоторой области изменения переменной х.

называется функциональным рядом, общий член ряда.

Так же как и для числовых рядов, сумма n первых членов ряда (1) называется его частичной суммой

Частичная сумма также является функцией от x. Из определения области сходимости функционального ряда следует, что для любой точки х этой области существует предел при Этот предел называется суммой функционального ряда (1). Очевидно, что в области сходимости ряда его сумма будет функцией от х. Обозначим ее S(x).

Разность между суммой ряда и его частичной суммой называется остатком

ряда и обозначается

Ясно, что Остаток ряда также является рядом, полученным из ряда (1) отбрасыванием n первых его членов.

Пример 1.Функциональный ряд

Для установления на практике равномерной сходимости функциональных рядов это определение мало пригодно. Обычно применяется достаточные признаки равномерной сходимости функциональных рядов. Одним из таких признаков является признак Вейерштрасса.

Теорема Вейерштрасса.Если члены функционального ряда (1) удовлетворяют в области сходимости неравенствам

Сходящейся числовой ряд называется мажорантным (мажорирующим) рядом (или мажорантой).

2.Если члены равномерно сходящиеся на отрезке функционального ряда непрерывны на этом отрезке, то сумму ряда можно почленно интегрировать.

Источник

Мажорируемые ряды

Функциональные ряды.

О.Ряд вида 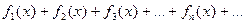(1) называется функциональным.

При каждом фиксированном х ряд(1) превращается в числовой, который может сходиться или расходиться.

Существует общая область определения для всех функций.

О.Множество тех значений х, при которых ряд (1) сходится называется областью сходимости этого ряда.

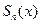
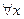
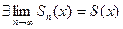
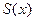
Если — частичная сумма ряда тогда из области сходимости ряда , где — сумма ряда.

Т.1. Если ряд (1) мажорируемый в области D, то он сходится в этой области абсолютно.

О.2. Ряд (1) – равномерно сходящийся в области D, если

—выполняется условие

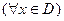
или .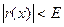

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Мажорирующий ряд

Добра, наставьте оболтуса на путь истинный, пытаюсь решить задачку:
Для данного функционального ряда построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке:

Я тут немного помозговал и вывел такой мажорирующий ряд (верно?):

Ok, терь надо исследовать ряд на сходимость?:

Вобщем, сомневаюсь, что верно получается, спасите.

Построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке
((sqrt(x+1))(cos(n*x)))/((sqrtn((n^5+1),3)))

Разложить в ряд Маклорена заданную фунцию f(x), используя ряд Макларена для ее производной
Разложить в ряд Маклорена заданную фунцию f(x), используя ряд Макларена для ее производной, и найти.

Пытаюсь мозговать дальше:

Предел стремится к 1

Добавлено через 7 минут
Неверно я предел вычисляю, видать.

В заданном массиве найти мажорирующий элемент
Задан массив длины n, найдите его мажорирующий элемент. Элемент называется мажорирующим, если он.

Необходлимо определить, есть ли в массиве мажорирующий элемент, и если есть, то какой
Мажорирующим элементом в массиве А будем называть элемент, встречающийся в массиве более n/2 раз.

Вычисление приближенного значения tan(x) через ряд Тейлора/ряд Маклорена
Привет, CF. Задача: Вычисление приближенного значения tan(x) через ряд Тейлора/ряд Маклорена.

Источник

Свойства мажорируемых рядов

(без доказательства)

Теорема 2: Если ряд из непрерывных функций мажорируем, то этот ряд можно почленно интегрировать.

Пусть ряд сходится и имеет некоторую сумму в области D:

, тогда: , где .

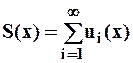
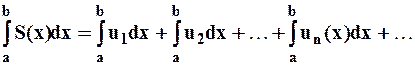
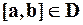
(Или: Если ряд, составленный из производных сходящегося ряда, мажорируем, то последний можно почленно дифференцировать).

Пример 4. Рассмотрим ряд:

. Данный ряд мажорируемый и его сумма есть непрерывная функция, но ряд, составленный из производных:

расходится, т.к. .

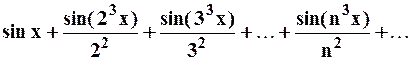
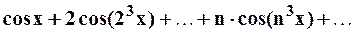
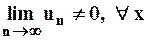
Рассмотрим важнейший класс мажорируемых рядов, которые называются степенными рядами.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник