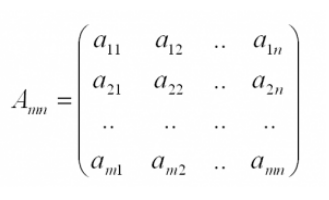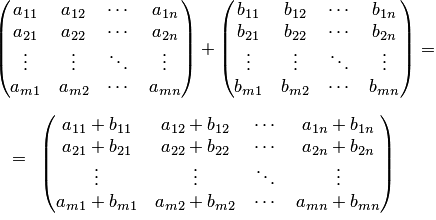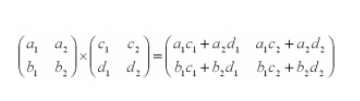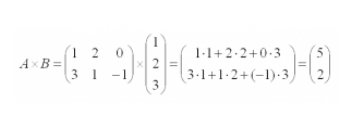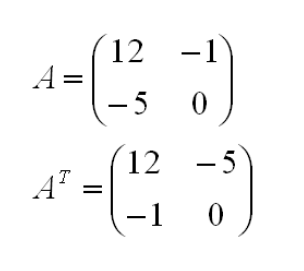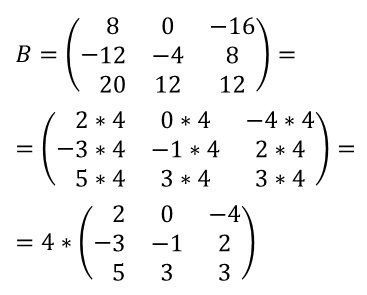что такое матрица в строительстве
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Что такое матрица: как складывать и умножать матрицы, чтобы не запутаться
Представьте: сидите на паре, погрязнув в огромных формулах, нить рассуждений потеряна, и вы уже не понимаете, о чем идет речь. Знакомое ощущение? Вот именно. Чтобы вы не упускали самую суть вещей, мы подготовили объяснение некоторых непростых тем простыми словами.
А чтобы вообще всегда были в курсе событий, подписывайтесь на наш телеграм-канал.
Что такое матрицы
Сегодня поговорим о матрицах. Пройти через эту тему предстоит, наверное, всем студентам, изучающим высшую математику (линейную алгебру, точнее говоря).
Именно с матриц начинается большинство курсов высшей математики. И пусть вас не пугает слово высшая. На самом деле, все не так страшно. Смотрите сами.
Матрица – это таблица. Таблица чисел, или букв, за которыми скрываются числа.
Матрицы могут быть разного размера: квадратные, прямоугольные, есть матрицы, состоящие всего из одной строки или одного столбца (горизонтальные и вертикальные).
Размер матрицы определяется количеством строк m и столбцов n. Номера строк и столбцов – буквами i и j соответственно.
А теперь, что еще нужно в первую очередь знать о работе с матрицами.
Как складывать матрицы
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера.
Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример.
Вычитание выполняется по аналогии, только вместо плюса пишем минус.
Как умножать матрицы
Во-первых, запомните: матрицу А можно умножить на матрицу B, только если если число столбцов матрицы А равно числу строк матрицы В.
При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м.
Вместо букв в матрице могут стоять реальные числа. Вот что получится, если умножить такие матрицы:
Можно и просто умножить матрицу на число. Для этого каждый ее элемент умножается на это число.
Что такое транспонированная матрица
Транспонировать матрицу – значит поменять строки и столбцы местами.
Вот как будет выглядеть матрица из самого первого примера, если ее транспонировать. Сама операция транспонирования обозначается индексом Т.
Что такое детерминант матрицы
Детерминант – это определитель – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко. А если часто, то с этим справятся специалисты студенческого сервиса. Обращайтесь, они помогут!
Анастасия Бабина. В моей фамилии часто ставят ударение на «И», но я привыкла. Копирайтер и редактор компании Zaochnik. Любительница мистических триллеров, отчаянный киноман и гурман в хорошей форме.
Что такое матрица в математике простыми словами
Обновлено: 08 Августа 2021
Матрица имеет множество значений в разных областях науки и техники. Конкретно в математике это объект, который облегчает вычисления и позволяет легко систематизировать любую информацию. Именно поэтому так необходимо знать, как ею пользоваться. Что же такое матрица?
Что такое матрицы в математике
Матрица — это таблица элементов, которая состоит из строк (m) и столбцов (n).
Может иметь разные размеры и формы в зависимости от количества находящихся в ней элементов. Элементы фиксированы: если переставить хотя бы один, то получится иная матрица с иными свойствами.
Откуда они взялись, чем полезны
Первые упоминания найдены еще в Древнем Китае, однако широкую известность матрицы приобрели только в середине XVIII, аккурат после выхода книги «Введение в анализ алгебраических кривых» Габриэля Крамера. В своей работе знаменитый математик описал совершенно новый способ решения систем линейных уравнений, который прозвали «методом волшебных квадратов». Сам термин «матрица» появился лишь в XIX веке благодаря трудам английского математика Д.Д. Сильвестра.
В современном мире матрицы используют повсюду. Телефонные справочники, табели успеваемости, отчеты и счета тоже являются матричными моделями. Они полезны, так как имеют прикладное значение.
Основные определения и обозначения матриц
В большинстве случаев матрицы обозначают прописными латинскими буквами (A, B, C), а ее элементы — строчными.
Виды матриц зависят от количества строк m и столбцов n. Основные из них:
Также существует понятие детерминант — это определитель свойств квадратной матрицы, который чаще всего используют в решении систем линейных алгебраических уравнений (СЛАУ).
Применение матриц в математико-экономическом моделировании
В математико-экономическом моделировании матрицы считаются самым удобным способом хранения различных структурированных данных и решения задач с ними. Приведем простой пример из экономической модели «затраты-выпуск».
Дана таблица распределения ресурсов по различным отраслям:
Так, элемент а23 = 5,8 обозначает то, сколько водных ресурсов потребляется в торговле, а элемент а11 = 4,8 обозначает, сколько трудовых ресурсов потребляется в промышленности.
Данная матрица может использоваться при сравнении и оценке востребованности ресурсов в различных отраслях экономики, решении экономических задач предприятий и организаций, анализе затраченных средств в ходе производства.
Решение матриц, основные операции с примерами и объяснением
Матрицы можно складывать и вычитать, умножать на определенное число, умножать между собой. Подробнее остановимся на основных операциях.
Сложение и вычитание матриц
Сложение и вычитание матриц возможно только в том случае, если они равны по размеру.
Чтобы сложить две матрицы, нужно сложить их соответствующие элементы.
С вычитанием действуем аналогичным образом.
Умножение матрицы на число
Чтобы умножить целую матрицу на число, необходимо умножить каждый элемент матрицы на это число.
Подметим, что дроби вносить в матрицу не нужно, поскольку это затрудняет дальнейшие операции.
Вынесение общего множителя за знак матрицы
Для вынесения общего множителя за знак матрицы необходимо найти общий множитель для всех элементов.
Подметим, что вынести общий множитель из строки или столбца невозможно.
Вынесение знака (минуса) за матрицу
При выполнении различных действий с матрицами большое количество минусов может привести к ошибкам и просчетам, поэтому обычно их выносят за матричную модель. Делается это при помощи замены всех знаков элементов. К примеру:
Таким образом, вероятность путаницы уменьшается за счет увеличения положительных коэффициентов.
Изучение матричных моделей не самое простое занятие. Если у вас нет времени на учебу, Феникс.Хелп может помочь в написании контрольных работ, статей и диссертаций. Переходите по ссылке и получаете квалифицированную помощь прямо сейчас!
Работа с Матрицей
Что такое Матрица судьбы?
В первую очередь это инструмент для самопознания, основанный на нумерологии, Таро и других методиках развития личности.
Метод называют по-разному: Матрица судьбы, Метод 22 Арканов, Матрица 22 энергий, Диагностика предназначения.
С помощью этого инструмента, по дате рождения можно узнать о своих или чужих качествах человека, узнав как текут/работают энергии, в плюсе или в минусе, можно узнать о сильных и слабых сторонах, о причинах поведения и реакций человека в каких-либо жизненных ситуациях.
Что означают цифры в Матрице?
22 Энергии Матрицы судьбы, расшифровываются/трактуются как и карты Таро, за тем исключением, что карты Таро читают как «прямая карта» и «перевернутая карта», а в Матрице, как указание на работу энергий в плюсе или минусе.
Как самому рассчитать Матрицу?
Матрица считается по нумерологическому принципу 22-ух, это закон цикличности, один цикл состоит из 22-ух ступеней.
В век прогресса, не нужно изобретать велосипед и считать все вручную на листке бумаги, можно воспользоваться нашим онлайн-калькулятором по автоматическому расчету Матрицы судьбы и формированию диаграммы. Для расчета Матрицы онлайн, нужна всего лишь дата рождения.
Как читать Матрицу/диаграмму?
На схемах ниже, изображены основные зоны Матрицы судьбы, участвующие в расшифровке!
Помимо зон указанных на схемах, в матрице есть и другие зоны, зоны пересекающиеся на примере зон «Кармический хвост», «Отношения», «Финансы», «Таланты от Бога», «Таланты от родителей» и т.д. т.п..
Как понять, работает энергия в Матрице в плюсе или минусе?
Кликнув по номеру Энергии на диаграмме рассчитанной с помощью онлайн-калькулятора, открывается окно с коротким описанием Энергии, где зеленым цветом перечислены проявления качеств человека указывающих на работу энергии в плюсе и красным, если в минусе.
Возьмите лист бумаги, перепишите эти качества в две колонки и в эмоционально балансном состоянии (без излишней радости или гнева), без контроля сознания и анализа, честно ответьте себе, какие из качеств человека указанных в списке, проявлены в вас.
Это примитивный, но простой и для многих действенный способ, не для всех, так как не все могут отключить контроль сознания, оно их просто не отпускает.
Как вывести энергию в плюс?
Кликнув по номеру Энергии на диаграмме рассчитанной с помощью онлайн-калькулятора, открывается окно с коротким описанием Энергии, где после перечисления качеств человека указывающих на течение энергии, работу ее в плюсе или минусе, есть описание «урока», что нужно для вывода энергии в плюс.
Помимо этого, если вы проводили анализ своих качеств и выяснили что из минусовых проявлено в вас, в вашей жизни, было бы не лишним заняться ими, их проработкой.
Не ставьте «ширмы», не закрашивайте «заплесневелые стены» краской, не работайте с последствиями, а работайте с причинами.
Только проработав причины, поменяются последствия, следовательно ваша жизнь!
Что делать, если я все ровно ни чего не понимаю?
Если вы рассчитали матрицу самостоятельно и хотите во всем разобраться или получили расчет и расшифровку от меня, у вас есть вопросы, вам хочется самим все понять и увидеть, но вам нужен «ключ» и т.п., то вы всегда можете мне написать в любой из мессенджеров и как только я смогу, я постараюсь дать вам развернутый ответ.
Также я провожу личные консультации онлайн и занимаюсь кураторством/сопровождением вас на вашем пути. Прошу не принимать близко к сердцу, если я отказался от консультации или сопровождения, я стараюсь не растрачивать себя на пустые действия и беру в «работу» только тех, кому это нужно и кто делает результаты, движется.
Товарная матрица
Любой бизнес основан на наличии продуктов или услуг, предлагаемых потребителю. Для эффективного ведения дел необходимо провести расширенный анализ рынка и составить товарную матрицу магазина, наполняя ассортимент торговой точки таким образом, чтобы полностью удовлетворить спрос клиентов и закрыть их основные потребности.
Товарная матрица (product grid) — это полный классифицированный список товаров, с которых складывается ассортимент конкретной точки продаж. Она составляется до открытия магазина и представляет собой таблицу или сетку с наименованиями позиций, объединенных по общему признаку.
Виды товаров в матрице
3 основных аспекта при составлении матрицы товаров
Создание оптимального товарного набора основано на трех столбах: ориентации на покупательский спрос, местоположении магазина и логистической карте поставок. Рассмотрим подробнее каждый пункт.
Ориентация на клиента
Разработка ассортиментной политики проходит после глубокого анализа целевой аудитории и ориентируется не только на общие характеристики платежеспособности и бюджета, но и на конкретные данные: пол, возраст, семейный статус, место жительства, доход, размер среднего чека. Такой подход позволит составить список товаров, необходимых большинству покупателей, и обеспечит стабильный поток клиентов в магазин.
Следует учитывать конкуренцию и развитость рынка, так как четкое разделение покупателей на группы выгодно в мегаполисах, где идет борьба за определенный социальный слой населения. Тогда как магазины в небольших городах и провинциях ориентируются на удовлетворение спроса широко круга, делая ассортимент больше, но не столь глубоким. Как пример можно привести мини-маркет, где предлагают всё от хлеба до бытовой химии, но количество брендов для каждой категории не превышает 2-3 видов или вовсе представлено в единичном варианте.
Местоположение торговой точки
На составление матрицы товаров влияет не только общее географическое положение, но и локальные характеристики, поэтому обратите внимание на особенности региона, район и локации, расположенные рядом с вашим объектом. Здесь же нужно учитывать площадь точки и объем продукции, которые можно здесь разместить, не создавая беспорядок и пресыщение потребителя.
При наличии торговой сети необходимо заранее учитывать возможность общего администрирования ассортиментных матриц и возможность быстрого перемещения товаров между филиалами.
Система поставок
На этапе составления Product Grid обратите внимание на разные виды закупок: оптовые, местные изготовители, уникальные предложения. Например, в местах с повышенной миграцией населения хорошо продаются товары узнаваемых по всей стране брендов, тогда как в других районах предпочтение отдают местным небольшим производствам.
В любом случае не должно быть перебоев и сложностей в доставке к точке. Особенное внимание нужно уделить мониторингу качества новой продукции.
При составлении матрицы товаров важно также ознакомиться с понятиями высоты, ширины и глубины ассортимента для корректной проработки товарного предложения.
7 этапов формирования Product Grid
Качественно проработанная товарная матрица с учетом сегментации потребителей и анализа рынка позволяет ускорить выход на точку безубыточности и максимально снижает риск излишних расходов и нерентабельности магазина.
Управление товарной матрицей магазина должно быть гибким и идти в ногу с запросами потребителей. Собирайте обратную связь, выявляйте наличие сезонных и других закономерностей, чтобы быстро корректировать ассортимент и не упускать клиентов.
Ошибки при разработке матрицы
При формировании Product Grid на стадии бизнес-идеи предприниматели часто делают ряд типичных ошибок, которые проявляются при старте дела и ведут к убыточным процессам. Чтобы избежать издержек и расходов не допускайте:
Образец товарной матрицы
Для создания сетки можно использовать готовый образец excel таблицы, так как такой вариант является оптимальным и легко читаемым. В таблицу в обязательном порядке включаются следующие пункты:
Вы можете скачать пример товарной матрицы в своей нише и отредактировать под свои запросы.
Удобно также использовать расширенную схему, где указывается цена закупки, размер наценки и показатели приоритетности товаров. В таком случае наиболее рентабельные единицы расписываются подробно с указанием всех параметров (широта, глубина, цена).
Учитывайте стратегические цели предприятия, формат магазина, местоположение, особенности и характер предполагаемой целевой аудитории с самого начала формирования ассортимента. Это позволит сократить время на последующие корректировки матрицы.