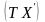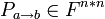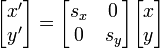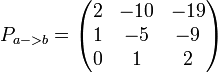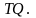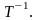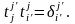что такое матрица перехода

Матрица перехода

Ма́трицей перехо́да от базиса к базису является матрица, столбцы которой — координаты разложения векторов в базисе .

Обозначается

Содержание

Представление

. . . .

Матрица перехода это

Использование

При умножении матрицы, обратной к матрице перехода на столбец, составленный из коэффициентов разложения вектора по базису , мы получаем тот же вектор, выраженный через базис .

Из-за того, что матрица перехода уменьшает объём работы при переводе векторов аффинных пространств и в пространстве столбцов в другие базисы, она используется в трёхмерном моделировании.

Пример

Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:

Относительно OX на угол φ

Относительно OY на угол ψ

Против часовой стрелки

Относительно OZ на угол χ

Матрицы наиболее распространённых преобразований
В двумерных координатах	В однородных двумерных координатах	В однородных трёхмерных координатах
Масштабирование
Поворот По часовой стрелке
Перемещение В неоднородных координатах не имеет матричного представления.

Свойства

Пример поиска матрицы

Найдём матрицу перехода от базиса к единичному базису путём элементарных преобразований

следовательно

См. также

Ссылки

Полезное

Смотреть что такое «Матрица перехода» в других словарях:

Матрица Лесли — Матрица перехода от n го шага популяционной модели к n+1 му. Произведение матрицы Лесли на вектор характеризующий численность популяции в n й момент времени в результате даст вектор характеризующий численность популяции n+1 й момент времени.… … Википедия

Матрица поворота — Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения … Википедия

Матрица переходных вероятностей — Цепь Маркова последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова … Википедия

Матрица вращения — Содержание 1 Матрица поворота в двумерном пространстве 2 Матрица поворота в трёхмерном пространстве … Википедия

Матрица направляющих косинусов — Содержание 1 Матрица поворота в двумерном пространстве 2 Матрица поворота в трёхмерном пространстве … Википедия

МАТРИЦА РАССЕЯНИЯ — (S матрица), совокупность величин (матрица), описывающая процесс перехода квантовомеханич. систем из одних состояний в другие при их вз ствии (рассеянии). Понятие «М. р.» введено нем. физиком В. Гейзенбергом в 1943. При вз ствии система переходит … Физическая энциклопедия

матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. [http://www.vidimost.com/glossary.html] матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика

Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь

Матрица плотности — (оператор плотности, оператор матрица плотности, статистический оператор) один из способов описания состояния квантовомеханической системы. В отличие от волновой функции, пригодной лишь для описания чистых состояний, оператор плотности в… … Википедия

Матрица рассеяния — Содержание 1 История 2 В технике СВЧ 2.1 Определение … Википедия

Источник

Матрицы перехода

У этого термина существуют и другие значения, см. Матрицы переходных вероятностей.

Обозначается

Содержание

Представление

. . . .

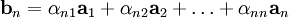
Матрица перехода это

Использование

Из-за того, что уменьшает объём работы при переводе векторов аффинных пространств и в пространстве столбцов R n в другие базисы, используется в трёхмерном моделировании.

Поворот вектора в двухмерном пространстве

Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить его на матрицу поворота:

Аналогично для поворота по часовой стрелке:

Изменение

Можно изменить длину вектора, умножив его на матрицу:

Свойства

Пример поиска матрицы

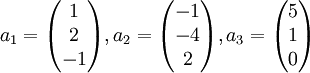
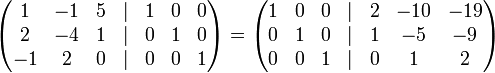
найдём матрицу перехода от базиса к единичному базису путём элементарных преобразований

следовательно

См. также

Ссылки

Полезное

Смотреть что такое «Матрицы перехода» в других словарях:

Разложение матрицы — Разложение матрицы представление матрицы в виде произведения матриц, обладающих некоторыми определёнными свойствами, например, ортогональностью, симметричностью, диагональностью и потому облегчающих рассмотрение свойств линейного… … Википедия

Подобные матрицы — Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что: Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных… … Википедия

Подобные матрицы — квадратные матрицы (См. Матрица) А и В порядка n, связанные соотношением В = Р 1АР, где Р какая либо неособенная (т. е. имеющая обратную) матрица того же порядка. При задании матрицей линейного преобразования (См. Линейное преобразование) … Большая советская энциклопедия

скорость выщелачивания радионуклидов из цементной матрицы — 3.3 скорость выщелачивания радионуклидов из цементной матрицы: Скорость перехода радионуклидов в растворитель при контакте с последним. Источник: ГОСТ Р 51883 2002: Отходы радиоактивные цементированные. Общие технические требования … Словарь-справочник терминов нормативно-технической документации

ГИПЕРБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ — численные методы решения методы решения уравнений гииерболпч. типа на основе вычислительных алгоритмов. Различные математич. модели во многих случаях приводят к дифференциальным уравнениям гиперболич. типа. Такие уравнения имеют точные аиалитич.… … Математическая энциклопедия

Матрица поворота — Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения … Википедия

Источник

Координаты и преобразования координат в линейном пространстве

Координаты векторов в данном базисе линейного пространства

Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.

Линейные операции в координатной форме

1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.

3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.

Преобразование координат вектора при замене базиса

Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.

Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:

Проверим результат, вычисляя по формуле (8.11):

Свойства матрицы перехода от одного базиса к другому

Действительно, запишем связь (8.10) для данных базисов:

3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.

В самом деле, справедливо разложение

Найдем координаты вектора в базисе двумя способами

Полученный результат подтверждает разложение:

Источник

Матрица перехода

Матрицы процессов также используются для расчета динамического развития в будущем. Однако, в отличие от стохастических матриц, они не обязательно должны иметь сумму строк или столбцов, равную единице. Однако, как и стохастическая матрица, они квадратные.

содержание

Дальнейшее различие

характеристики

Собственные значения и собственные векторы

Это особенно актуально, когда элементы стохастической матрицы действительно больше 0.

Выпуклость, нормы и замкнутость

Непосредственно из определения следует, что норма суммы строк стохастической матрицы строк равна 1, как и норма суммы столбцов стохастической матрицы столбцов.

Пример переходной матрицы P

Приложение для характеризации дискретных цепей Маркова

Для стохастических матриц столбцов можно действовать аналогично, только умножение векторов выполняется справа, а обычный собственный вектор вычисляется с собственным значением 1. В качестве альтернативы вы также можете транспонировать матрицу и использовать процедуру, описанную выше.

Кроме того, многие свойства цепи Маркова также можно найти в матрице перехода:

Примеры

Крыса в комнате

Теперь Питер выпускает крысу и хочет узнать вероятность того, что крыса окажется в клетке через 20 минут. Начальное состояние системы

(крыса находится в клетке с вероятностью 1). Состояние через 20 минут (после 4 временных шагов) будет (округлено)

Значит, крыса находится в клетке с вероятностью 0,0952.

Так что Питеру следует сначала заглянуть за шкаф.

Кот и мышка

Матрица перехода A для этого теперь

Источник

Свойства матрицы перехода

1º. Матрица перехода от одного базиса к другому определяется однозначно.

►Вытекает из того, что она состоит из координатных столбцов векторов одного базиса в другом.◄

2º. Матрица перехода всегда невырождена.

►На основании матричного критерия линейной независимости.◄

3º. Если Т – невырожденная квадратная матрица n-го порядка и

такой, что Т – матрица перехода от (3.46) к (3.47).

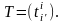
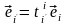
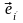
►Пусть Положим (т. е. – вектор, чей координатный столбец в базисе (3.46) совпадает с i-м столбцом матрицы Т). Тогда (3.47) – линейно независимая система на основании матричного критерия, а значит, в является базисом. Из определения матрицы перехода вытекает, что Т – матрица перехода от (3.46) к (3.47).◄

4º. Матрица перехода от базиса к нему самому является единичной.

►Доказательство вытекает из равенства .◄

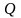
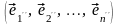
5º. Если Т – матрица перехода от базиса (3.46) к базису (3.47),а — матрица перехода от (3.47) к базису

, (3.48)

то матрицей перехода от (3.46) к (3.48) является матрица

►Действительно, 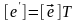, , и поэтому . Утверждение вытекает из определения матрицы перехода.◄

6º. Если Т – матрица перехода от (3.46) к (3.47), то матрицей перехода от (3.47) к (3.46) является

►(3.45) 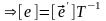, и утверждение опять вытекает из определения матрицы перехода.◄

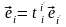
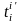
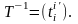
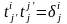
Замечание. По аналогии с равенством (3.44) естественно записать равенство , и поэтому элементы матрицы перехода от (3.47) к (3.46) естественно обозначать . Учитывая, что эта матрица есть не что иное, как получаем: Так как и то и

14. Определение матрицы перехода. Изменение координат вектора при изменении базиса. Изменение координат вектора при изменении базиса

. (3.49)

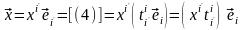
Равенство (3.49) – это разложение вектора по базису (3.46), и поэтому в силу единственности координат вектора в данном базисе получаем

. (3.50)

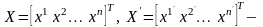
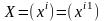
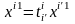
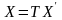
Обозначим координатные столбцы вектора в базисах (3.46) и (3.47) соответственно ( , ). Тогда (3.50) равносильно равенству , из которого вытекает, что

. (3.51)

Формулы (3.50) и (3.51) показывают, как изменяются координаты вектора при изменении базиса. Равенство (3.51) можно доказать и так:

.

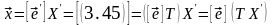
Таким образом, – координатный столбец вектора в базисе (3.46), поэтому он совпадает с .

Источник