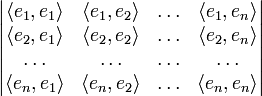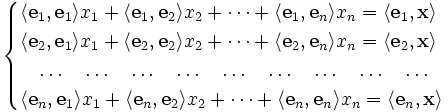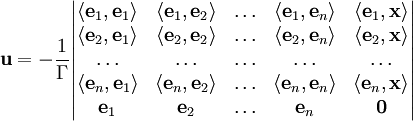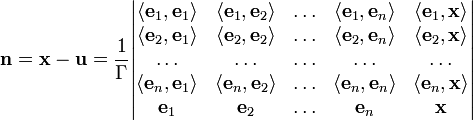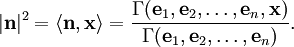что такое матрица грама

Матрица и определитель Грама: определение, свойства, приложения

Определение матрицы Грама

Изменение матрицы Грама при переходе от одного базиса к другому

По формуле (8.32) вычислим скалярное произведение векторов [math]\mathbf[/math] и [math]\mathbf[/math] в разных базисах:

Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :

Определитель Грама и его свойства

Определитель матрицы [math]G(\mathbf_1,\mathbf_2,\ldots, \mathbf_n)[/math] называется определителем Грама. Рассмотрим свойства этого определителя.

1. Критерий Грама линейной зависимости векторов: система векторов [math]\mathbf_1,\mathbf_2, \ldots, \mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.

Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.

Главный минор матрицы Грама системы [math]\mathbf_1, \mathbf_2,\ldots,\mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.

Действительно, в процессе ортогонализации по векторам [math]\mathbf_1,\mathbf_2, \ldots,\mathbf_k[/math] последовательно строятся векторы

После первого шага определитель Грама не изменяется

Так как при этих преобразованиях определитель не изменяется, то

Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:

3. Определитель Грама любой системы [math]\mathbf_1,\mathbf_2,\ldots, \mathbf_k[/math] векторов удовлетворяет двойному неравенству

Следовательно, по свойству 2 имеем

1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.

2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.

Метрические приложения определителя Грама

[math]V_<\ast \boldsymbol_1>=|\boldsymbol_1|[/math] — одномерный объем — длина вектора [math]\boldsymbol_1[/math] ;

[math]V_<\ast \boldsymbol_1,\boldsymbol_2>= V_<\ast \boldsymbol_1>\cdot |\boldsymbol_2|= |\boldsymbol_1|\cdot|\boldsymbol_2|[/math] — двумерный объем — площадь параллелограмма, построенного на векторах [math]\boldsymbol_1,\,\boldsymbol_2[/math] ;

[math]V_<\ast \boldsymbol_1,\boldsymbol_2, \boldsymbol_3>= V_<\ast \boldsymbol_1, \boldsymbol_2>\cdot |\boldsymbol_3|= |\boldsymbol_1|\cdot |\boldsymbol_2|\cdot |\boldsymbol_3|[/math] — трехмерный объем — объем параллелепипеда, построенного на векторах [math]\boldsymbol_1,\,\boldsymbol_2,\, \boldsymbol_3[/math] ;

т.е. определитель Грама векторов [math]\boldsymbol_1, \boldsymbol_2, \ldots, \boldsymbol_k[/math] равен квадрату k-мерного объема параллелепипеда, построенного на этих векторах. В этом заключается геометрический смысл определителя Грама.

Аналогично определяется расстояние от конца вектора до многообразия.

Углом между ненулевым вектором [math]\boldsymbol[/math] и подпространством [math]L[/math] называется наименьший угол [math]\varphi[/math] между вектором [math]\boldsymbol[/math] и ненулевыми векторами подпространства, т.е.

Аналогично определяется угол между вектором и многообразием, как угол между вектором и однородной частью многообразия.

Из неравенств пункта 1 замечаний 8.14 следует, что

Для нахождения расстояний и углов можно использовать формулу (8.37).

а угол [math]\varphi[/math] между ненулевым вектором [math]\boldsymbol[/math] и подпространством находится по формуле

Пример 8.22. В пространстве [math]\mathbb^4[/math] со стандартным скалярным произведением (8.27) заданы: вектор [math]v=\begin-3&2&0&0\end^T[/math] и подпространство [math]L[/math] — множество [math]\[/math] решений однородной системы:

Решение. Базис подпространства был найден в примере 8.9:

Источник

Матрица Грама

где — скалярное произведение векторов e_i и e_j.

Матрица Грама возникает из следующей задачи линейной алгебры:

Геометрический смысл определителя Грама

Геометрический смысл определителя Грама раскрывается при решении следующей задачи:

и квадрат его модуля равен

Из этой формулы индукцией по n получается следующее утверждение:

Полезное

Смотреть что такое «Матрица Грама» в других словарях:

ГРАМА МАТРИЦА — квадратная матрица составленная из попарных скалярных произведений элементов (векторов) (пред)гильбертова пространства. Г. м. всегда неотрицательна. Она положительно определена, если а 1, а 2. а k линейно независимы. Справедливо обратное:… … Математическая энциклопедия

Положительно определённая матрица — В линейной алгебре, положительно определённая матрица это эрмитова матрица, которая во многом аналогична положительному вещественному числу. Это понятие тесно связано с положительно определённой симметрической двулинейной формой (или… … Википедия

Отрицательно определённая матрица — В линейной алгебре, положительно определённая матрица это эрмитова матрица, которая во многом аналогична положительному вещественному числу. Это понятие тесно связано с положительно определённой симметрической двулинейной формой (или… … Википедия

Отрицательно полуопределённая матрица — В линейной алгебре, положительно определённая матрица это эрмитова матрица, которая во многом аналогична положительному вещественному числу. Это понятие тесно связано с положительно определённой симметрической двулинейной формой (или… … Википедия

Положительно полуопределённая матрица — В линейной алгебре, положительно определённая матрица это эрмитова матрица, которая во многом аналогична положительному вещественному числу. Это понятие тесно связано с положительно определённой симметрической двулинейной формой (или… … Википедия

Определитель Грама — Определителем Грама (англ.) (грамианом) системы векторов в евклидовом пространстве называется определитель матрицы Грама этой системы … Википедия

Источник