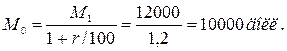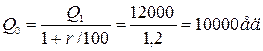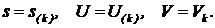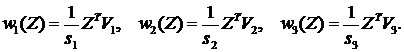что такое математическая формализация задачи

Математический формализм

Полезное

Смотреть что такое «Математический формализм» в других словарях:

Формализм (матем.) — Формализм в математике, см. Математический формализм … Большая советская энциклопедия

Формализм — I Формализм (франц. formalisme, от лат. formalis – относящий к форме) предпочтение, отдаваемое форме перед содержанием в различных сферах человеческой деятельности (см. Содержание и форма). В области человеческих отношений Ф. проявляется… … Большая советская энциклопедия

Математический интуиционизм — философско математическое течение, отвергающее теоретико множественную трактовку математики и считающее интуицию единственным источником математики и главным критерием строгости её построений. Восходящая к античной математике… … Большая советская энциклопедия

Формализм — (от лат. forma) 1) предпочтение, отдаваемое форме перед содержанием; 2) соблюдение внешней формы в ущерб существу дела; 3) тот или иной математический прием, лежащий в основе какой либо науки, раздела науки, конкретный формализм используемый в… … Начала современного естествознания

ИНТУИЦИОНИЗМ (математический) — одно из направлений в философии математики (Л. Кронекер, А. Пуанкаре, Л. Брауэр, Г. Рейтинг), представители которого предложили новую концепцию предмета и обоснования математики, резко противопоставив ее не только эмпиристской, объективно… … Философия науки: Словарь основных терминов

МАТЕМАТИКА — наука, или группа наук, о познаваемых разумом многообразиях и структурах, специально – о математических множествах и величинах; напр., элементарная математика – наука о числовых величинах (арифметика) и величинах пространственных (геометрия) и о… … Философская энциклопедия

ТЕОРИЯ — (от греч. theoria рассмотрение, исследование) совокупность высказываний, замкнутых относительно логического следования. Такое предельно общее и наиболее абстрактное определение Т. дает логика. С логической т.зр. теорией можно назвать любое… … Философская энциклопедия

Гамильтонова механика — Классическая механика … Википедия

Состояние (квантовая механика) — У этого термина существуют и другие значения, см. Состояние. Квантовая механика Принцип неопределённости Гейзенберга … Википедия

Источник

Математическая формализация

Для исследования характеристик процесса функционирования любой системы математическими методами, включая и компьютерное моделирование, должна быть проведена формализация этого процесса, то есть построена математическая модель. Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее устанавливать ее свойства, характеризующие, в конечном счете, свойства моделируемого объекта.

Вид математической модели зависит от природы реального объекта, задач исследования, требуемой достоверности и точности решения этих задач, наконец, от вкуса и квалификации исследователя.

Модель – это условный образ исследуемого объекта, который приближенно воссоздает этот объект с помощь некоторого языка. В экономико-математических моделях таким объектом является экономический процесс (например, планирование производства, использование мощностей и др.), а языком – математические методы.

Экономико-математическая модель – это математическое описание исследуемого экономического процесса или объекта.

Примерами экономико-математических моделей являются модели потребительского выбора, модели фирмы, модели экономического роста, модели равновесия на товарных, факторных и финансовых рынках и другие. При построении моделей экономисты выявляют существенные факторы, которые определяют исследуемое явление, и отбрасывают детали, несущественные для решения поставленной проблемы. Формализация основных особенностей функционирования экономических объектов позволяет оценить возможные последствия воздействия на них и использовать такие оценки в управлении.

Применение математического моделирования при принятии решений предполагает последовательное осуществление трех этапов исследования.

Первый – от исходной практической проблемы до теоретической чисто математической задачи.

Второй – математическое изучение и решение этой задачи.

Третий – переход от математических выводов обратно к практической проблеме.

В области моделирования задач принятия решений, как и в иных областях применения математики, выделяют четверку проблем: задача – модель – метод – условия применимости.

Задача, как правило, порождена потребностями той или иной прикладной области. При этом происходит одна из возможных математических формализаций реальной ситуации. Например, при изучении предпочтений потребителей у маркетологов возникает вопрос: различаются ли мнения двух групп потребителей?

При математической формализации мнения потребителей в каждой группе обычно моделируются как независимые случайные выборки, т.е. как совокупности независимых одинаково распределенных случайных величин. Вопрос маркетологов в рамках этой модели переформулируется в вопрос о проверке той или иной статистической гипотезы однородности, например, о проверке равенства математических ожиданий или о совпадении функций распределения двух совокупностей.

Задача может возникнуть при обобщении потребностей ряда прикладных областей. Необходимости проверки упомянутой гипотезы однородности возникает и в медицине при сравнении двух групп пациентов, в технике при сопоставлении результатов обработки деталей двумя способами и в других областях. Следовательно, одна и та же математическая модель может применяться для решения разных по прикладной сущности задач.

Другими словами, следует различать математическую структуру модели и ее экономическое содержание. Рассмотрим два простых примера[2].

Пример 1. Пусть требуется определить, какую сумму следует положить в банк при заданной ставке процента (20 % годовых), чтобы через год получить 12000долл.?

Введем формальные обозначения для величин рассматриваемой задачи:

М₀ – начальная сумма денег;

М₁ – конечная сумма денег;

r – ставка процента.

Запишем соотношение между ними (математическую модель):

Найдем требуемую величину из решения основного уравнения модели:

Пример 2. Пусть требуется определить, каков был объем выпуска продукции предприятия, если в результате технического перевооружения средняя производительность труда увеличилась на 20 %, и предприятие стало выпускать 12000 единиц продукции.

Введем формальные обозначения для величин рассматриваемой задачи:

r – процент прироста производительности.

Запишем соотношение между ними (математическую модель):

Найдем требуемую величину из решения основного уравнения модели:

Сравнивая полученные модели и результаты, можно заметить, что математическая форма модели имеет вид:

который является одинаковым для обоих примеров, как и числовые значения входящих в нее величин и результатов. Однако экономическая ситуация, описываемая моделью и экономическое содержание модели и результатов расчета совершенно различны. Таким образом, одни и те же математические модели и методы могут быть использованы для решения совершенно разных экономических задач.

Метод, используемый в рамках определенной математической модели – это дело математиков. Для решения задачи в рамках одной и той же принятой исследователем модели может быть предложено много методов. Например, центральная предельная теорема теории вероятностей была получена такими разными методами, как: теорема Муавра – Лапласа, метод моментов Чебышева, метод характеристических функций Ляпунова, метод Линдеберга и метод Феллера. Для проверки гипотезы однородности могут использоваться методы Смирнова, Лемана – Розенблата, Вилкоксона и др.

Условия применимости – полностью математический элемент четверки. С точки зрения математика замена условия дифференцируемости некоторой функции на условие ее непрерывности представляет существенное научное достижение, в то время как для прикладного исследователя, как и во времена Ньютона и Лейбница, непрерывные функции мало отличаются от дифференцируемых. Точнее, они одинаково могут быть использованы для описания реальной действительности.

Экономические модели позволяют выявить особенности функционирования экономического объекта и на основе этого предсказывать будущее поведение объекта при изменении каких-либо параметров. Предсказания будущих изменений, например, повышение обменного курса, ухудшения экономической конъюнктуры, падение прибыли может опираться только на интуицию. Но при этом могут быть упущены, неправильно определены или неверно оценены важные взаимосвязи экономических показателей, влияющих на рассматриваемую ситуацию. В модели все взаимосвязи переменных могут быть оценены количественно, что позволяет получить более качественный и надежный прогноз.

По своему определению любая экономическая модель абстрактна и, следовательно, неполна, поскольку она включает наиболее существенные факторы, определяющие закономерности функционирования рассматриваемого экономического объекта, она абстрагируется от других факторов, которые, несмотря на свою относительную малость, все же в совокупности могут определять не только отклонения в поведении объекта, но и само его поведение. Так, в простейшей модели спроса считается, что величина спроса на товар определяется его ценой и доходом потребителя. На самом же деле на величину спроса оказывает также влияние ряд других факторов: вкусы и ожидания потребителей, цены на другие товары, воздействие рекламы, моды и т.п. Обычно предполагают, что все факторы, не учтенные явно в экономической модели, оказывают на объект относительно малое результирующее воздействие в интересующем исследователя аспекте. Состав учтенных в модели факторов и ее структура могут быть уточнены в ходе совершенствования модели.

Источник

Математическая формализация

Для исследования характеристик процесса функционирования любой системы математическими методами, включая и компьютерное моделирование, должна быть проведена формализация этого процесса, то есть построена математическая модель. Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее устанавливать ее свойства, характеризующие, в конечном счете, свойства моделируемого объекта.

Вид математической модели зависит от природы реального объекта, задач исследования, требуемой достоверности и точности решения этих задач, наконец, от вкуса и квалификации исследователя.

Модель – это условный образ исследуемого объекта, который приближенно воссоздает этот объект с помощь некоторого языка. В экономико-математических моделях таким объектом является экономический процесс (например, планирование производства, использование мощностей и др.), а языком – математические методы.

Экономико-математическая модель – это математическое описание исследуемого экономического процесса или объекта.

Примерами экономико-математических моделей являются модели потребительского выбора, модели фирмы, модели экономического роста, модели равновесия на товарных, факторных и финансовых рынках и другие. При построении моделей экономисты выявляют существенные факторы, которые определяют исследуемое явление, и отбрасывают детали, несущественные для решения поставленной проблемы. Формализация основных особенностей функционирования экономических объектов позволяет оценить возможные последствия воздействия на них и использовать такие оценки в управлении.

Применение математического моделирования при принятии решений предполагает последовательное осуществление трех этапов исследования.

Первый – от исходной практической проблемы до теоретической чисто математической задачи.

Второй – математическое изучение и решение этой задачи.

Третий – переход от математических выводов обратно к практической проблеме.

В области моделирования задач принятия решений, как и в иных областях применения математики, выделяют четверку проблем: задача – модель – метод – условия применимости.

Задача, как правило, порождена потребностями той или иной прикладной области. При этом происходит одна из возможных математических формализаций реальной ситуации. Например, при изучении предпочтений потребителей у маркетологов возникает вопрос: различаются ли мнения двух групп потребителей?

При математической формализации мнения потребителей в каждой группе обычно моделируются как независимые случайные выборки, т.е. как совокупности независимых одинаково распределенных случайных величин. Вопрос маркетологов в рамках этой модели переформулируется в вопрос о проверке той или иной статистической гипотезы однородности, например, о проверке равенства математических ожиданий или о совпадении функций распределения двух совокупностей.

Задача может возникнуть при обобщении потребностей ряда прикладных областей. Необходимости проверки упомянутой гипотезы однородности возникает и в медицине при сравнении двух групп пациентов, в технике при сопоставлении результатов обработки деталей двумя способами и в других областях. Следовательно, одна и та же математическая модель может применяться для решения разных по прикладной сущности задач.

Другими словами, следует различать математическую структуру модели и ее экономическое содержание. Рассмотрим два простых примера[2].

Пример 1. Пусть требуется определить, какую сумму следует положить в банк при заданной ставке процента (20 % годовых), чтобы через год получить 12000долл.?

Введем формальные обозначения для величин рассматриваемой задачи:

М₀ – начальная сумма денег;

М₁ – конечная сумма денег;

r – ставка процента.

Запишем соотношение между ними (математическую модель):

Найдем требуемую величину из решения основного уравнения модели:

Пример 2. Пусть требуется определить, каков был объем выпуска продукции предприятия, если в результате технического перевооружения средняя производительность труда увеличилась на 20 %, и предприятие стало выпускать 12000 единиц продукции.

Введем формальные обозначения для величин рассматриваемой задачи:

r – процент прироста производительности.

Запишем соотношение между ними (математическую модель):

Найдем требуемую величину из решения основного уравнения модели:

Сравнивая полученные модели и результаты, можно заметить, что математическая форма модели имеет вид:

который является одинаковым для обоих примеров, как и числовые значения входящих в нее величин и результатов. Однако экономическая ситуация, описываемая моделью и экономическое содержание модели и результатов расчета совершенно различны. Таким образом, одни и те же математические модели и методы могут быть использованы для решения совершенно разных экономических задач.

Метод, используемый в рамках определенной математической модели – это дело математиков. Для решения задачи в рамках одной и той же принятой исследователем модели может быть предложено много методов. Например, центральная предельная теорема теории вероятностей была получена такими разными методами, как: теорема Муавра – Лапласа, метод моментов Чебышева, метод характеристических функций Ляпунова, метод Линдеберга и метод Феллера. Для проверки гипотезы однородности могут использоваться методы Смирнова, Лемана – Розенблата, Вилкоксона и др.

Условия применимости – полностью математический элемент четверки. С точки зрения математика замена условия дифференцируемости некоторой функции на условие ее непрерывности представляет существенное научное достижение, в то время как для прикладного исследователя, как и во времена Ньютона и Лейбница, непрерывные функции мало отличаются от дифференцируемых. Точнее, они одинаково могут быть использованы для описания реальной действительности.

Экономические модели позволяют выявить особенности функционирования экономического объекта и на основе этого предсказывать будущее поведение объекта при изменении каких-либо параметров. Предсказания будущих изменений, например, повышение обменного курса, ухудшения экономической конъюнктуры, падение прибыли может опираться только на интуицию. Но при этом могут быть упущены, неправильно определены или неверно оценены важные взаимосвязи экономических показателей, влияющих на рассматриваемую ситуацию. В модели все взаимосвязи переменных могут быть оценены количественно, что позволяет получить более качественный и надежный прогноз.

По своему определению любая экономическая модель абстрактна и, следовательно, неполна, поскольку она включает наиболее существенные факторы, определяющие закономерности функционирования рассматриваемого экономического объекта, она абстрагируется от других факторов, которые, несмотря на свою относительную малость, все же в совокупности могут определять не только отклонения в поведении объекта, но и само его поведение. Так, в простейшей модели спроса считается, что величина спроса на товар определяется его ценой и доходом потребителя. На самом же деле на величину спроса оказывает также влияние ряд других факторов: вкусы и ожидания потребителей, цены на другие товары, воздействие рекламы, моды и т.п. Обычно предполагают, что все факторы, не учтенные явно в экономической модели, оказывают на объект относительно малое результирующее воздействие в интересующем исследователя аспекте. Состав учтенных в модели факторов и ее структура могут быть уточнены в ходе совершенствования модели.

Дата добавления: 2014-12-03 ; просмотров: 144 ; Нарушение авторских прав

Источник

Математическая формализация задачи

Постановка задачи

С чего начать? Прежде всего, нужно разобраться, что дано, что требуется получить, как связаны исходные данные и результаты. Иначе говоря, задача должна быть четко сформулирована.

Четко сформулировать задачу — это значит высказать те предположения об изучаемом явлении или объекте, которые позволят выявить исходные данные, определить, что будет служить результатом, и какова связь между исходными данными и результатом.

Под постановкой задачи понимают математическую или иную строгую формулировку решаемой задачи. На этом этапе должно быть четко определено, что дано, и что требуется найти. Так, если задача конкретная, то под постановкой задачи понимают ответ на два вопроса: какие исходные данные известны и что требуется определить. Если задача обобщенная, то при постановке задачи понадобится еще ответ на третий вопрос: какие данные допустимы.

Таким образом, постановка задачи включает в себя следующие моменты:

· сбор информации о задаче; формулировку условия задачи;

· определение конечных целей решения задачи;

· определение формы выдачи результатов;

· описание данных (их типов, диапазонов величин, структуры и т. п.).

При постановке задачи должны быть определены требования:

· ко времени решения поставленной задачи;

· объему необходимых ресурсов, например, оперативной памяти;

· точности достигаемого результата.

Постановка задачи — важная часть (иногда говорят — половина) ее решения.

В случае большого числа параметров, ограничений, возможных вариантов исходных данных модель явления может иметь очень сложное математическое описание (правда, реальное явление еще более сложно), поэтому часто построение математической модели требует упрощения требований задачи. Необходимо выявить самые существенные свойства объекта, явления или процесса, закономерности; внутренние связи, роль отдельных характеристик. Выделив наиболее важные факторы, можно пренебречь менее существенными.

Составить хорошую математическую модель задачи непросто. Всякое явление природы бесконечно в своей сложности. Проиллюстрируем это с помощью примера, взятого из книги В.Н. Тростникова «Человек и информация» (М.: «Наука», 1970):

— Позвольте, — может сказать «заказчик», — меня не устраивает такое упрощение. Я хочу знать точно, сколько времени будет падать камень в реальных условиях, а не в несуществующей пустоте.

— Хорошо, — согласится математик. — Будем считать, что камень имеет сферическую форму и диаметр. Какого примерно он диаметра?

— Около пяти сантиметров. Но он вовсе не сферический, а продолговатый.

— Тогда будем считать, что он имеет форму эллипсоида с полуосями четыре, три и три сантиметра и что он падает так, что большая полуось все время остается вертикальной. Давление воздуха примем равным 760 мм ртутного столба, отсюда найдем плотность воздуха.

Если тот, кто поставил задачу на «человеческом» языке не будет дальше вмешиваться в ход мысли математика, то последний через некоторое время даст численный ответ. Но «потребитель» может возражать по-прежнему: камень на самом деле вовсе не эллипсоидальный, давление воздуха в том месте и в тот момент не было равно 760 мм ртутного столба и т.д.

Что же ответит ему математик? Он ответит, что точное решение реальной задачи вообще невозможно.

Мало того, что форму камня, которая влияет на сопротивление воздуха, невозможно описать никаким математическим уравнением, его вращение в полете также неподвластно математике из-за своей сложности. Далее, воздух не является однородным, так как в результате действия случайных факторов в нем возникают флуктуации колебания плотности. Если пойти ещё глубже, нужно учесть, что по закону всемирного тяготения каждое тело действует на каждое другое тело. Отсюда следует, что даже маятник настенных часов изменяет своим движением траекторию камня.

Короче говоря, если мы всерьез захотим точно исследовать поведение какого-либо предмета, то нам предварительно придется узнать местонахождение и скорость всех остальных предметов Вселенной. А это, разумеется, невозможно…

Итак, создавая математическую модель для решения задачи, нужно:

· выделить предположения, на которых будет основываться математи­ческая модель;

· определить, что считать исходными данными и результатами;

· записать математические соотношения, связывающие результаты с исходными данными.

Для разработки алгоритма необходимо на основании математической модели определить состав, тип и допустимые значения обрабатываемых данных, выбрать способ их использования и способ установки значений.

Выбор типа данных, способов их использования и способ установки значений значительно влияют на структуру алгоритма решения задачи. Неправильныйвыбор типов данных излишне усложняет алгоритм решения задачи, увеличивает время выполнения программы, а неправильный выбор способа использования данных или способа установки их значений усложняет отладку и модификацию программы.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Математическая формализация задачи

Отнесение различных векторов индикаторов к одному классу может рассматриваться как агрегация исходных данных, при этом геометрическая близость (расстояние) между объектами формализуется с помощью соответствующей векторной нормы. Наиболее распространенной является евклидова норма:

.

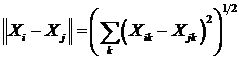
Следовательно, задача обучения сводится к разбиению пространства индикаторов на классы (т.е. к проведению классификации), а задача распознавания сводится к определению класса (т.е. к проведению кластеризации) z_j=_j, j=1,…,k с помощью выбранной векторной нормы:

.

Как известно, с помощью векторной нормы можно определить понятие расстояния между вектором и классом, а также понятие расстояния между классами.

С точки зрения распознавания образов полагается, что чем меньше значение выбранной нормы, тем сходство между объектами больше.

Определим образ как n-мерный вектор-столбец X=[x₁, x₂,…,x_n], где x₁, x₂,…,x_n являются вещественными числами, и индекс T является символом транспонирования матрицы.

Представим задачу распознавания образовкак отображение f(X)→ любого образа X в одно из целых чисел 1,…,c, которые представляют классы.

Задача распознавания образов может быть сформулирована следующим образом:

— набор из m обучающих образов: X1,….,Xm;;

— класс любого обучающего образа:f(X1)=c1…,f(Xm)=cm;

— произвольный n-мерный вектор P.

Класс вектора P: f(P)=?.

Для реальных задач исходные данные в самом общем случае являются многомерными и допускают представление в виде массивов (векторов) вещественных и/или целых чисел. Как было отмечено выше, одной из основных особенностей ИК-алгоритма распознавания образов является проекция произвольных данных в пространство ФИС. Такое преобразование обладает следующими преимуществами:

— имеет строгое математическое обоснование в терминах сингулярного разложения матриц;

— существенно снижает размерность данных (до одно- двух- или трехмерного пространства ФИС);

— позволяет наглядно представить и визуализировать любую ситуацию как точку одно- двух- или трехмерного пространства.

Рассмотрим математическое описание основных процедур алгоритма иммунокомпьютинга.

Обучение

1. Сформировать обучающую матрицу A=[X₁,…,X_m] T размерности m×n.

2. Вычислить максимальное сингулярное число s, а также левый и правый сингулярные векторы U и V обучающей матрицы по следующей итеративной (эволюционной) схеме:

до выполнения условия

3. Хранить сингулярное число s.

4. Хранить правый сингулярный вектор V как антитело-пробу.

5. Для всякого i=1,…,m хранить компоненту u_i левого сингулярного вектора U (как клетку формальной иммунной сети) и класс c_i, соответствующий обучающему образу X_i.

Распознавание

6. Для всякого n-мерного образа Z вычисляется энергия связи с V:

(напомним, что s–хранимое сингулярное число, а V– это хранимый правый сингулярный вектор обучающей матрицы A).

7. Выбирается u_i, которая имеет минимальное расстояние (близость) с энергией связи w:

8. Считать класс c_i искомым классом образа Z.

Замечания

Данное ядро алгоритма распознавания образов использует только максимальное (первое) сингулярное число s и соответствующие ему сингулярные векторы U и V, которые вычисляются на шаге 2 данного алгоритма.

В общем случае, рекомендуется использовать первые три сингулярных числа и соответствующие им сингулярные векторы обучающей матрицы. Они могут быть вычислены по той же итеративной схеме (шаг 2) с использованием вычислительной процедуры метода исчерпывания:

1.Вычислить максимальное сингулярное число s₁ и соответствующие ему сингулярные вектора U₁ и V₁ обучающей матрицы на шаге 2.

2.Сформировать матрицу A₂=A‑s₁U₁V₁ и вычислить ее максимальное сингулярное число s₂ и соответствующие ему сингулярные векторы U₂ и V₂ посредством шага 2.

3.Сформировать матрицу A₃=A – s₂U₂V₂ и вычислить ее максимальное сингулярное число s₃ и соответствующие ему сингулярные векторы U₃ и V₃ посредством шага 2.

Затем вычислить 3 значения энергии связи с помощью шага 6:

Определить класс c_i на шаге 8 посредством определения минимального расстояния в трехмерном Евклидовом пространстве на шаге 7:

,

где являются i-ми компонентами левых сингулярных векторов U₁, U₂, U₃.

Отметим, что шаги 2 и 3 над матрицами A₂ и A₃ обеспечивают более точную аппроксимацию обучающей матрицы, согласно следующему свойству сингулярного разложения:

где – ранг матрицы A.

Следует также отметить, что данный алгоритм иммунокомпьютинга может быть рассмотрен как «иммунный» алгоритм, так как любой образ может быть представлен как частный случай формального протеина и его распознавание основывается на энергии связи с антителом формального протеина.

Лабораторная работа № 4

Цель работы:создание программного модуля для реализации вычислительной процедуры обучения с экспертом на основе инструментария универсальной системы MATLAB.

Порядок выполнения работы

1. Открыть универсальную систему MATLAB.

2. Задать исходную матрицу А соответствующейразмерности и матрицу анализируемого объекта М. Программно реализовать шаги 1-8 алгоритма вычислительной процедуры обучения с экспертом.

3. Сохранить все результаты выполнения работы в файле на диске.

4.5.2. Порядок оформления отчета

Отчетом о лабораторной работе № 4 является файл с именем, совпадающим с фамилией студента с результатами работы в папке Мои документы/номер группы.

Пример выполнения лабораторной работы №4

Рассмотрим решение задачи классификации (задачи обучения с экспертом) на примере классификации легковых автомобилей.

Пусть имеется обучающая выборка в виде матрицы R размерности (3×33). Эта матрица в качестве элементов имеет индикаторы, характеризующие три класса легковых автомобилей (второй, пятый и шестой):

Рисунок 19 Обучающая выборка в виде матрицы R размерности (3×33).

Сингулярное разложение обучающей матрицы R осуществляется c помощью оператора: [U S V]=svd(R).

Ниже представлены матрицы компонент сингулярного разложения:

Рисунок 20 Матрицы компонент сингулярного разложения

Анализируемый объект представляется в виде вектора М:

M=[2000 3 1375 1925 222 10.1 445 4547 1766 1428 2650 1528 106 3 2 1781 9.5 2 20 150 210 2 1 3 2 2 2 2 11.3 6.4 9.2 1 71].

Для этого вектора М вычисляем значения энергии связи и расстояние до соответствующих точек для 2, 5, 6, классов в пространстве ФИС.

Рисунок 21 Результаты вычислений значений энергии

Из полученного множества значений расстояний от точки в пространстве ФИС, характеризуемой анализируемый объект до точек, характеризующих соответственно, классы 2, 5, 6:

выбираем наименьшее значение, которое равно 0.4082. Это значение определяет принадлежность анализируемого объекта к 5 классу.

Вывод: анализируемый объект принадлежит к 5 классу.

4.5.4. Контрольные вопросы

1. Какая норма была использована при проведении классификации?

2. Сущность вычислительной процедуры автоматической классификации.

3. Можно ли назвать рассмотренную процедуру обучения с экспертом интеллектуальной процедурой?

ФОРМИРОВАНИЕ ИНДЕКСОВ РИСКА

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник