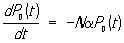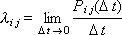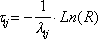что такое марковский процесс
Марковский процесс
Ма́рковский проце́сс — случайный процесс, эволюция которого после любого заданного значения временно́го параметра 

Содержание
История
Определяющее марковский процесс свойство принято называть марковским; впервые оно было сформулировано А. А. Марковым, который в работах 1907 г. положил начало изучению последовательностей зависимых испытаний и связанных с ними сумм случайных величин. Это направление исследований известно под названием теории цепей Маркова.
Однако уже в работе Л. Башелье можно усмотреть попытку трактовать броуновское движение как марковский процесс, попытку, получившую обоснование после исследований Винера в 1923.
Основы общей теории марковских процессов с непрерывным временем были заложены Колмогоровым.
Отличие Марковского процесса от Марковской цепи
Марковская цепь с дискретным временем — время дискретно, пространство состояний дискретно.
Марковская цепь с непрерывным временем — время непрерывно, пространство состояний дискретно
Марковский процесс — и время и пространство состояний непрерывно.
См. также
Ссылки
Полезное
Смотреть что такое «Марковский процесс» в других словарях:
МАРКОВСКИЙ ПРОЦЕСС — процесс без последействия, случайный процесс, эволюция к рого после любого заданного значения временного параметра tне зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано (короче: будущее н… … Математическая энциклопедия
МАРКОВСКИЙ ПРОЦЕСС — важный специальный вид случайных процессов. Примером марковского процесса может служить распад радиоактивного вещества, где вероятность распада данного атома за малый промежуток времени не зависит от течения процесса в предшествующий период.… … Большой Энциклопедический словарь
Марковский процесс — 36. Марковский процесс Примечания: 1. Условную плотность вероятности называют плотностью вероятности перехода из состояния xn 1в момент времени tn 1 в состояние хпв момент времени tn. Через нее выражаются плотности вероятностей произвольного… … Словарь-справочник терминов нормативно-технической документации
марковский процесс — Markovo procesas statusas T sritis automatika atitikmenys: angl. Markovprocess vok. Markovprozeß, m rus. марковский процесс, m; процесс Маркова, m pranc. processus markovien, m … Automatikos terminų žodynas
марковский процесс — Markovo vyksmas statusas T sritis fizika atitikmenys: angl. Markov process; Markovian process vok. Markow Prozeß, m; Markowscher Prozeß, m rus. марковский процесс, m; процесс Маркова, m pranc. processus de Markoff, m; processus marcovien, m;… … Fizikos terminų žodynas
Марковский процесс — важный специальный вид случайных процессов. Примером Марковского процесса может служить распад радиоактивного вещества, где вероятность распада данного атома за малый промежуток времени не зависит от течения процесса в предшествующий период.… … Энциклопедический словарь
Марковский процесс — важный специальный вид случайных процессов (См. Случайный процесс), имеющих большое значение в приложениях теории вероятностей к различным разделам естествознания и техники. Примером М. п. может служить распад радиоактивного вещества.… … Большая советская энциклопедия
МАРКОВСКИЙ ПРОЦЕСС — выдающееся открытие в области математики, сделанное в 1906 русским ученым А.А. Марковым. Источник: Энциклопедия Русская цивилизация … Русская история
Марковский процесс
Полезное
Смотреть что такое «Марковский процесс» в других словарях:
МАРКОВСКИЙ ПРОЦЕСС — процесс без последействия, случайный процесс, эволюция к рого после любого заданного значения временного параметра tне зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано (короче: будущее н… … Математическая энциклопедия
МАРКОВСКИЙ ПРОЦЕСС — важный специальный вид случайных процессов. Примером марковского процесса может служить распад радиоактивного вещества, где вероятность распада данного атома за малый промежуток времени не зависит от течения процесса в предшествующий период.… … Большой Энциклопедический словарь
Марковский процесс — 36. Марковский процесс Примечания: 1. Условную плотность вероятности называют плотностью вероятности перехода из состояния xn 1в момент времени tn 1 в состояние хпв момент времени tn. Через нее выражаются плотности вероятностей произвольного… … Словарь-справочник терминов нормативно-технической документации
марковский процесс — Markovo procesas statusas T sritis automatika atitikmenys: angl. Markovprocess vok. Markovprozeß, m rus. марковский процесс, m; процесс Маркова, m pranc. processus markovien, m … Automatikos terminų žodynas
марковский процесс — Markovo vyksmas statusas T sritis fizika atitikmenys: angl. Markov process; Markovian process vok. Markow Prozeß, m; Markowscher Prozeß, m rus. марковский процесс, m; процесс Маркова, m pranc. processus de Markoff, m; processus marcovien, m;… … Fizikos terminų žodynas
Марковский процесс — важный специальный вид случайных процессов. Примером Марковского процесса может служить распад радиоактивного вещества, где вероятность распада данного атома за малый промежуток времени не зависит от течения процесса в предшествующий период.… … Энциклопедический словарь
МАРКОВСКИЙ ПРОЦЕСС — выдающееся открытие в области математики, сделанное в 1906 русским ученым А.А. Марковым. Источник: Энциклопедия Русская цивилизация … Русская история
Лекция 33.
Моделирование марковских случайных
процессов
Очень удобно описывать появление случайных событий в виде вероятностей переходов из одного состояния системы в другое, так как при этом считается, что, перейдя в одно из состояний, система не должна далее учитывать обстоятельства того, как она попала в это состояние.
Случайный процесс называется марковским процессом (или процессом без последействия ), если для каждого момента времени t вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, как система пришла в это состояние.
Итак, марковский процесс удобно задавать графом переходов из состояния в состояние. Мы рассмотрим два варианта описания марковских процессов с дискретным и непрерывным временем.
В первом случае переход из одного состояния в другое происходит в заранее известные моменты времени такты (1, 2, 3, 4, ). Переход осуществляется на каждом такте, то есть исследователя интересует только последовательность состояний, которую проходит случайный процесс в своем развитии, и не интересует, когда конкретно происходил каждый из переходов.
Во втором случае исследователя интересует и цепочка меняющих друг друга состояний, и моменты времени, в которые происходили такие переходы.
Марковский процесс с дискретным временем
| |
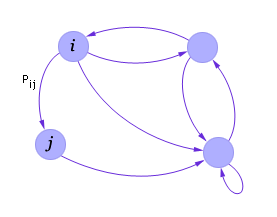
| Рис. 33.1. Пример графа переходов |
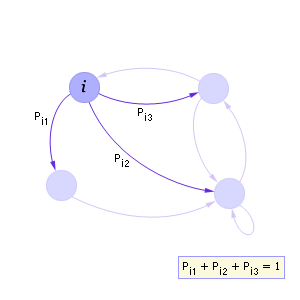
Ясно, что у каждого состояния сумма вероятностей всех переходов (исходящих стрелок) из него в другие состояния должна быть всегда равна 1 (см. рис. 33.2 ).
| |
| Рис. 33.2. Фрагмент графа переходов (переходы из i-го состояния являются полной группой случайных событий) |
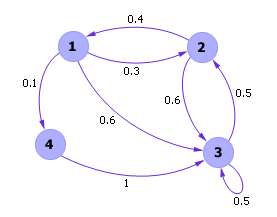
| |
| Рис. 33.3. Пример марковского графа переходов |
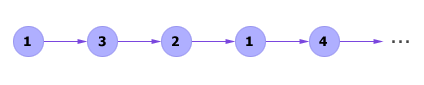
Реализация марковского процесса (процесс его моделирования) представляет собой вычисление последовательности (цепи) переходов из состояния в состояние (см. рис. 33.4 ). Цепь на рис. 33.4 является случайной последовательностью и может иметь также и другие варианты реализации.
| |
| Рис. 33.4. Пример марковской цепи, смоделированной по марковскому графу, изображенному на рис. 33.3 |
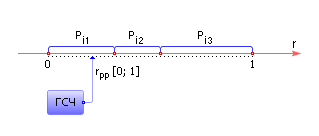
| |
| Рис. 33.5. Процесс моделирования перехода из i-го состояния марковской цепи в j-е с использованием генератора случайных чисел |
После этого осуществляется переход в состояние, определенное ГСЧ, и повтор описанной процедуры для нового состояния. Результатом работы модели является марковская цепь (см. рис. 33.4 ).
Определим следующие три состояния: S0 цель не повреждена; S1 цель повреждена; S2 цель разрушена. Зададим вектор начальных вероятностей:
|
Значение P0 для каждого из состояний показывает, какова вероятность каждого из состояний объекта до начала стрельбы.
Зададим матрицу перехода состояний (см. табл. 33.1).
| Таблица 33.1. Матрица вероятностей перехода дискретного марковского процесса | |||||||||||||||||||
|
Матрица задает вероятность перехода из каждого состояния в каждое. Заметим, что вероятности заданы так, что сумма вероятностей перехода из некоторого состояния в остальные всегда равна единице (куда-то система должна перейти обязательно).
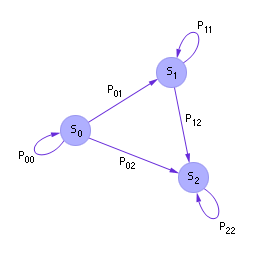
Наглядно модель марковского процесса можно представить себе в виде следующего графа (см. рис. 33.6 ).
| |
| Рис. 33.6. Граф марковского процесса, моделирующий стрельбу из пушки по цели |
Используя модель и метод статистического моделирования, попытаемся решить следующую задачу: определить среднее количество снарядов, необходимое для полного разрушения цели.
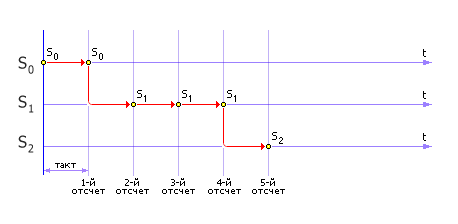
На рис. 33.7 приведена временная диаграмма, которая получается во время описанного процесса моделирования. Диаграмма показывает, как во времени происходит процесс изменения состояний. Такт моделирования для данного случая имеет фиксированную величину. Нам важен сам факт перехода (в какое состояние переходит система) и не важно, когда это происходит.
| |
| Рис. 33.7. Временная диаграмма переходов в марковском графе (пример имитации) |
Теперь следует определить точность. Именно точность может нам показать, насколько следует доверять данному ответу. Для этого проследим, как сходится последовательность случайных (приближенных) ответов к правильному (точному) результату. Напомним, что, согласно центральной предельной теореме (см. лекцию 25, лекцию 21), сумма случайных величин есть величина неслучайная, поэтому для получения статистически достоверного ответа необходимо следить за средним числом снарядов, получаемых в ряде случайных реализаций.
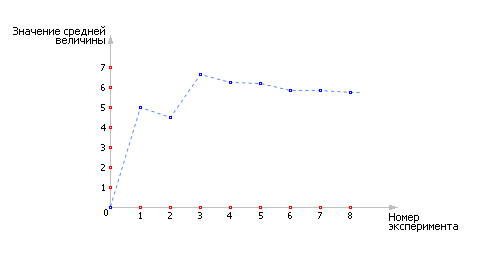
На первом этапе вычислений средний ответ составил 5 снарядов, на втором этапе средний ответ составил (5 + 4)/2 = 4.5 снаряда, на третьем (5 + 4 + 11)/3 = 6.7. Далее ряд средних величин, по мере накопления статистики, выглядит следующим образом: 6.3, 6.2, 5.8, 5.9, 5.8. Если изобразить этот ряд в виде графика средней величины выпущенных снарядов, необходимых для поражения цели, в зависимости от номера эксперимента, то обнаружится, что данный ряд сходится к некоторой величине, которая и является ответом (см. рис. 33.8 ).
| |
| Рис. 33.8. Изменение средней величины в зависимости от номера эксперимента |
Визуально мы можем наблюдать, что график «успокаивается», разброс между вычисляемой текущей величиной и ее теоретическим значением со временем уменьшается, стремясь к статистически точному результату. То есть в некоторый момент график входит в некоторую «трубку», размер которой и определяет точность ответа.
Алгоритм имитации будет иметь следующий вид (см. рис. 33.9).
Еще раз заметим, что в вышерассмотренном случае нам безразлично, в какие моменты времени будет происходить переход. Переходы идут такт за тактом. Если важно указать, в какой именно момент времени произойдет переход, сколько времени система пробудет в каждом из состояний, требуется применить модель с непрерывным временем.
Марковские случайные процессы с непрерывным временем
| |
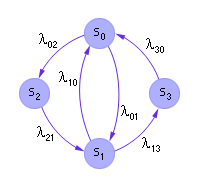
| Рис. 33.10. Пример графа марковского процесса с непрерывным временем |
При этом плотность понимают как распределение вероятности во времени.
К интенсивности переходов (здесь это понятие совпадает по смыслу с распределением плотности вероятности по времени t ) переходят, когда процесс непрерывный, то есть, распределен во времени.
С интенсивностью потока (а переходы это поток событий) мы уже научились работать в лекции 28. Зная интенсивность λij появления событий, порождаемых потоком, можно сымитировать случайный интервал между двумя событиями в этом потоке.
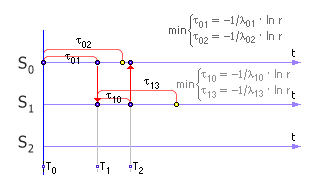
Реализация будет иметь следующий вид (см. рис. 33.11 ).
| |
| Рис. 33.11. Пример моделирования непрерывного марковского процесса с визуализацией на временной диаграмме (желтым цветом указаны запрещенные, синим реализовавшиеся состояния) |
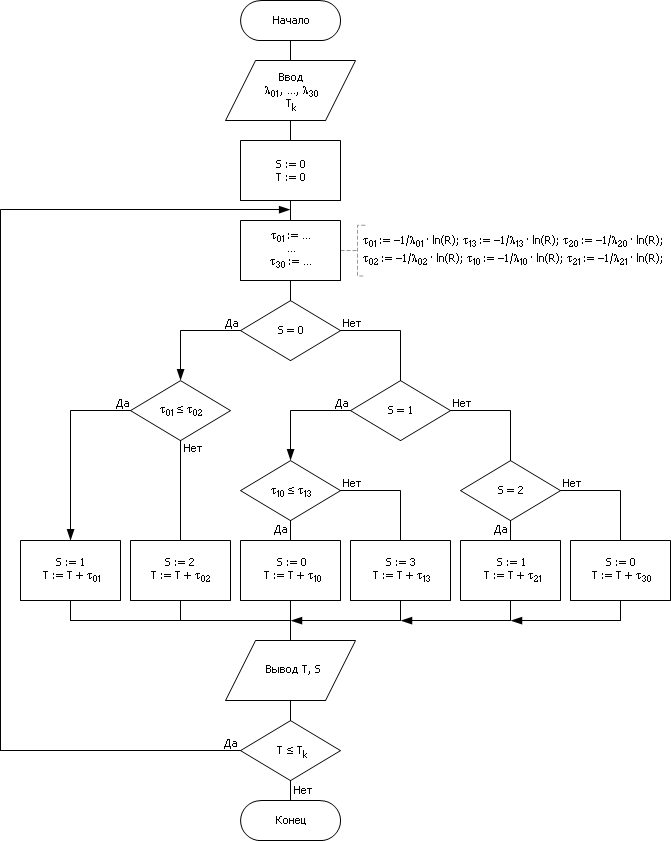
Алгоритм имитации будет иметь следующий вид (см. рис. 33.12 ).
| |
| Рис. 33.12. Блок-схема алгоритма моделирования непрерывного марковского процесса на примере имитации работы станка |
Очень часто аппарат марковских процессов используется при моделировании компьютерных игр, действий компьютерных героев.
Марковские процессы
История
Определяющее марковский процесс свойство принято называть марковским; впервые оно было сформулировано А. А. Марковым, который в работах 1907 г. положил начало изучению последовательностей зависимых испытаний и связанных с ними сумм случайных величин. Это направление исследований известно под названием теории цепей Маркова. Однако уже в работе Л. Башелье можно усмотреть попытку трактовать броуновское движение как марковский процесс, попытку, получившую обоснование после исследований Винера в 1923. Основы общей теории марковских процессов с непрерывным временем были заложены Колмогоровым.
Смотреть что такое «Марковские процессы» в других словарях:
Марковские процессы — вероятностные процессы, обладающие тем свойством, что при известном значении процесса в момент времени поведение процесса в более поздние моменты времени не зависит от его поведения до момента. Типичными примерами марковских процессов являются… … Начала современного естествознания
СКАЧКООБРАЗНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ — класс марковских случайныхпроцессов, у к рых значения изменяются мгновенно (скачки) в отдельные(случайные) моменты времени. В наиб. простом случае, когда марковский процесс может принимать лишь конечное или счётное число значений x1. х п … Физическая энциклопедия
МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ — процессы без вероятностного последствия, статистич. свойства к рых в последующие моменты времени зависят только от значений процессов в данный момент и не зависят от их предыстории. M.с … Физическая энциклопедия
ВЕРОЯТНОСТЕЙ ТЕОРИЯ — математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных к. л. образом с первыми. Утверждение о том, что к. л. событие наступает с вероятностью, равной, напр., 1/2, еще не… … Математическая энциклопедия
Вероятностей теория — математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким либо образом с первыми. Утверждение о том, что какое либо событие наступает с Вероятностью,… … Большая советская энциклопедия
МАРКОВСКИЙ ПРОЦЕСС — процесс без последействия, случайный процесс, эволюция к рого после любого заданного значения временного параметра tне зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано (короче: будущее н… … Математическая энциклопедия
Доказательства эволюции — Ископаемый археоптерикс, обнаруженный вскоре после публикации « … Википедия
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ — раздел математики, посвященный теории и методам решения многошаговых задач оптимального управления. В Д. п. для управляемых процессов среди всевозможных управлений ищется то, к рое доставляет экстремальное (наименьшее или наибольшее) значение… … Математическая энциклопедия
ЭКСЦЕССИВНАЯ ФУНКЦИЯ — для марковского процесса аналог неотрицательной супергармонической функции. Пусть в измеримом пространстве задана однородная марковская цепь с вероятностями перехода за один шаг Измеримая относительно функция наз. эксцессивной функцией для этой… … Математическая энциклопедия
МАРКОВСКИЙ ПРОЦЕСС
важный спец. вид случайных процессов. Примером М. п. может служить распад радиоактивного в ва, где вероятность распада данного атома за малый промежуток времени не зависит от течения процесса в предшествующий период. Теория М. п. возникла на основе иссл. А. А. Маркова (старшего) по теории вероятностей.
Смотреть что такое «МАРКОВСКИЙ ПРОЦЕСС» в других словарях:
МАРКОВСКИЙ ПРОЦЕСС — процесс без последействия, случайный процесс, эволюция к рого после любого заданного значения временного параметра tне зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано (короче: будущее н… … Математическая энциклопедия
МАРКОВСКИЙ ПРОЦЕСС — важный специальный вид случайных процессов. Примером марковского процесса может служить распад радиоактивного вещества, где вероятность распада данного атома за малый промежуток времени не зависит от течения процесса в предшествующий период.… … Большой Энциклопедический словарь
Марковский процесс — 36. Марковский процесс Примечания: 1. Условную плотность вероятности называют плотностью вероятности перехода из состояния xn 1в момент времени tn 1 в состояние хпв момент времени tn. Через нее выражаются плотности вероятностей произвольного… … Словарь-справочник терминов нормативно-технической документации
марковский процесс — Markovo procesas statusas T sritis automatika atitikmenys: angl. Markovprocess vok. Markovprozeß, m rus. марковский процесс, m; процесс Маркова, m pranc. processus markovien, m … Automatikos terminų žodynas
марковский процесс — Markovo vyksmas statusas T sritis fizika atitikmenys: angl. Markov process; Markovian process vok. Markow Prozeß, m; Markowscher Prozeß, m rus. марковский процесс, m; процесс Маркова, m pranc. processus de Markoff, m; processus marcovien, m;… … Fizikos terminų žodynas
Марковский процесс — важный специальный вид случайных процессов. Примером Марковского процесса может служить распад радиоактивного вещества, где вероятность распада данного атома за малый промежуток времени не зависит от течения процесса в предшествующий период.… … Энциклопедический словарь
Марковский процесс — важный специальный вид случайных процессов (См. Случайный процесс), имеющих большое значение в приложениях теории вероятностей к различным разделам естествознания и техники. Примером М. п. может служить распад радиоактивного вещества.… … Большая советская энциклопедия
МАРКОВСКИЙ ПРОЦЕСС — выдающееся открытие в области математики, сделанное в 1906 русским ученым А.А. Марковым. Источник: Энциклопедия Русская цивилизация … Русская история