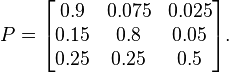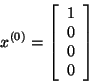что такое марковская цепь
Что такое цепи Маркова и как они работают
Простой способ сгенерировать много текста, который будет похож на настоящий.
В «Коде» уже вышло несколько проектов, где мы генерировали какой-то случайный текст, чтобы показать его пользователю:
Проблема с этими генераторами была в том, что нам вручную приходилось прописывать все варианты, последовательности и комбинации из слов и предложений. Чтобы добавить новый вариант в этих проектах, нужно зайти в код и вручную прописать новый текстовый блок в одной из переменных.
Главный минус такого подхода — вы делаете всю работу за компьютер. Вы сами жёстко задаёте структуру каждого предложения. Такой текст вас ничем не удивит, потому что вы чётко знаете, сколько предложений у вас в шаблоне и из каких частей состоит каждое.
Чтобы генерировать много похожего текста, но без таких заморочек, используют нейросети или алгоритмы на цепях Маркова. Нейросети пока оставим, а сегодня займёмся цепями.
Что такое цепь Маркова
Представьте, что у нас есть набор каких-то событий, связанных друг с другом. Например, первое наступает только после второго, второе — после третьего или четвёртого, а третье — после четвёртого с вероятностью 30% и так далее. Получается, что каждое новое событие зависит только от предыдущего и не зависит от всех остальных до него.
Допустим, у нас есть событие «Взять зонт», которое всегда идёт только после события «Идёт дождь». Даже если сейчас середина декабря, кругом снег, но внезапно случилась оттепель и пошёл дождь — следом за ним по этой логике будет событие «Взять зонт».
👉 Цепи Маркова — это последовательность событий или действий, где каждое новое событие зависит только от предыдущего и не учитывает все остальные события. Такой алгоритм не помнит, что было раньше, а смотрит только на предыдущее состояние.
Чтобы было понятнее, разберём на тексте.
Текст и цепи Маркова
Возьмём такую скороговорку:
Ехал грека через реку, видит грека — в реке рак, сунул грека руку в реку, рак за руку греку цап.
В теории цепей Маркова это называется корпус — исходный материал, по которому будут составляться взаимосвязи. В нашем случае по этому предложению мы поймём, как одни слова будут связаны с другими.
❗️ Для простоты мы опустим знаки препинания и большие буквы. В нормальных алгоритмах это, конечно, учитывается, но пока мы учимся, можно и так.
Наша задача — понять на этом примере, как устроены и как работают цепи Маркова. Для этого мы шаг за шагом смоделируем работу алгоритма и посмотрим, что получится в итоге.
Считаем слова
Посчитаем, сколько раз встречается каждое слово в нашем тексте:
Цепь Маркова
Jun 10 · 5 min read
Цепь Маркова используют многие современные компании и организации. Она помогает прогнозировать погоду и разрабатывать маркетинговые стратегии, находит применение в различных приложениях для решения реальных задач конечных автоматов, таких как DFA.
В Python эта концепция представлена в системе вероятностного автомата. Изменения состояния системы называются переходами. Вероятности, связанные с различными изменениями состояния, называются вероятностями перехода. Вероятностный автомат превращает вероятность каждого перехода в функцию перехода и формирует переходную матрицу.
Как создать цепь Маркова
Представим себе такую ситуацию:
“Когда Си Джей грустит (что для нее не очень характерно), она либо отправляется на пробежку, либо поглощает мороженое, либо укладывается спать”.
Для созда н ия цепи Маркова нам потребуется сначала создать переходную матрицу, в которой будут перечислены вероятности каждого перехода состояния. Другими словами, мы должны представить текущее состояние сегодняшним действием Си Джей, в то время как следующее состояние — ее завтрашним действием.
Вероятность перехода состояния будем рассматривать как вероятность того, что Си Джей выполнит одно из трех конкретных действий сегодня, а следующее действие, тоже одно, — завтра. Например, Си Джей отправится на пробежку сегодня, а завтра будет спать. Связав таким образом все вероятности перехода состояния, мы получим переходную матрицу, которая поможет создать цепь Маркова, описывающую конкретную ситуацию.
Наша матрица перехода — это матрица N x N, предполагающая, что N — это количество вероятных состояний. Итак, сначала мы должны определить количество состояний в нашей задаче. Поскольку нам дано три действия, которые Си Джей совершает, когда ей грустно, у нас есть 3 состояния. При этом важно учитывать, что Си Джей не может выполнять все 3 действия одновременно. Другими словами, она не может в одно и то же время спать и есть мороженое, так как ключевые слова в постановке задачи — либо одно действие, либо другое.
Главная идея цепи Маркова заключается в том, что существует только одно текущее состояние и, следовательно, один переход в одно следующее состояние. Это важное замечание поможет нам отслеживать наши вероятности.
Как уже говорилось выше, мы выделили 3 действия, которые совершает Си Джей, когда ей грустно, чтобы определить значение N, или количество состояний. Теперь мы должны создать переходную матрицу связанных вероятностей 3 х 3.
Пошаговый алгоритм процесса создания переходной матрицы
Предположим, что Си Джей грустит. В этом случае, как указано в задаче, нужно рассмотреть 3 вероятных состояния Си Джей:
Если текущее состояние “спит”, то можно вычислить вероятность следующего состояния:
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей спит в течение сегодняшнего дня.
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей спит. Вы можете видеть вероятность каждого перехода, например, когда Си Джей спит сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,6; съест мороженое — 0,2. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “собирается на пробежку”, то вероятность следующего состояния составит:
Мы выделили красным цветом строку, на которой сосредоточились, поскольку текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей собирается на пробежку в течение сегодняшнего дня.
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей собирается на пробежку. Вы можете видеть вероятности каждого перехода, например, когда Си Джей собирается на пробежку в текущий день, вероятность того, что на следующий день она будет спать, равна 0,1; пойдет на пробежку — 0,6; съест мороженое — 0,3. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “ест мороженое”, то вероятность следующего состояния составит:
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей ест мороженое в течение сегодняшнего дня.
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей ест мороженое. Вы можете видеть вероятность каждого перехода, например, когда Си Джей ест мороженое сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,7; съест мороженое — 0,1. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Ниже приведена конечная переходная матрица.
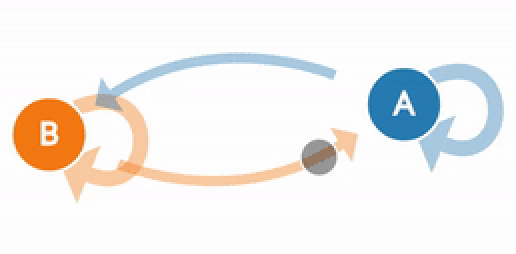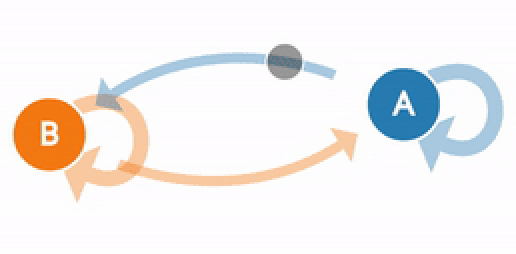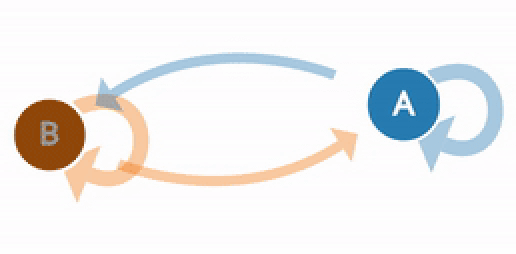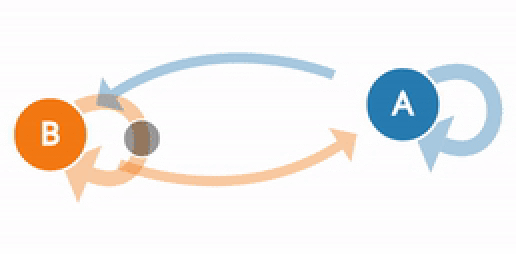
Используя конечную переходную матрицу, мы можем создать цепь Маркова. Для этого отметим все 3 состояния, представляющие ситуацию в настоящее время. Затем создадим переходы между состояниями. Направление стрелки определяет переход от текущего к следующему состоянию. Используя значения из нашей матрицы, подставляем их к соответствующим переходам состояния. Когда текущее состояние равно следующему состоянию, это означает, что Си Джей выполняет одно и то же действие в течение текущего и следующего дня. В этом случае стрелка возвращается к текущему состоянию, поскольку нет перехода в другое состояние.
Дополнительное упражнение
Теперь давайте еще раз взглянем на цепь Маркова, которая моделирует погоду (она была представлена в начале этого поста).
Попытайтесь на основе описанного выше алгоритма создать свою собственную переходную матрицу. Когда закончите, прокрутите страницу вниз, чтобы увидеть конечный результат!
Конечная переходная матрица
Ниже представлена переходная матрица цепи Маркова, которая моделирует погоду. Чтобы ее создать, мы использовали тот же алгоритм, что описан выше, только в обратном направлении.
Заключение
Как вы видели в приведенных выше примерах, цепь Маркова можно использовать в прогнозировании погоды, а также в разработке маркетинговой стратегии, основанной на предположении вероятного поведения потребителя. На основе цепей Маркова созданы такие приложения, как Google PageRank, Subreddit, генератор текстов, автозаполнение слов и предложений. Компании могут использовать эту концепцию для принятия сложных решений, поскольку она позволяет увидеть различные потенциальные решения в доступной визуализированной форме.
Интуитивное использование методов Монте-Карло с цепями Маркова.
Легко ли это? Я попробовал.
Алексей Кузьмин, директор разработки и работы с данными ДомКлик, преподаватель факультета « Аналитика и Data Science » в Нетологии, перевёл статью Rahul Agarwal о том, как работают методы Монте-Карло с цепями Маркова для решения проблем с большим пространством состояний.
Каждый, кто связан с Data Science, хоть раз слышал о методах Монте-Карло с цепями Маркова (MCMC). Иногда тема затрагивается во время изучения байесовской статистики, иногда — при работе с такими инструментами, как Prophet.
Но MCMC трудно понять. Всякий раз, читая об этих методах, я замечал, что суть MCMC скрыта в глубоких слоях математического шума, и за этим шумом её тяжело разобрать. Мне пришлось потратить много часов, чтобы разобраться в этой концепции.
В этой статье — попытка объяснить методы Монте-Карло с цепями Маркова доступно, так, чтобы стало понятно, для чего они используются. Я остановлюсь ещё на нескольких способах использования этих методов в моём следующем посте.
Итак, начнём. MCMC состоит из двух терминов: Монте-Карло и Марковские цепи. Поговорим о каждом из них.
Монте-Карло
Методы Монте-Карло получили своё название от казино Монте-Карло в Монако. Во многих карточных играх нужно знать вероятность выиграть у дилера. Иногда вычисление этой вероятности может быть математически сложным или трудноразрешимым. Но мы всегда можем запустить компьютерную симуляцию, чтобы много раз воспроизвести всю игру и рассматривать вероятность как количество побед, разделённое на количество сыгранных игр.
Это всё, что вам нужно знать о методах Монте-Карло. Да, это просто несложная техника моделирования с причудливым названием.
Марковские цепи
Поскольку термин MCMC состоит из двух частей, нужно ещё понять, что такое цепи Маркова. Но прежде, чем перейти к Марковским цепям, немного поговорим о Марковских свойствах.
Предположим, есть система из M-возможных состояний и вы переходите из одного состояния в другое. Пусть пока вас ничего не сбивает с толку. Конкретный пример подобной системы — погода, которая меняется от жаркой к холодной и умеренной. Другой пример — фондовый рынок, который прыгает от «медвежьего» к «бычьему» и состоянию стагнации.
Марковское свойство говорит о том, что для данного процесса, который находится в состоянии Xn в конкретный момент времени, вероятность Xn + 1= k (где k — любое из M-состояний, в которое процесс может перейти) зависит только от того, каково это состояние в данный момент. А не о том, как оно достигло нынешнего состояния.
Говоря математическим языком, можем записать это в виде следующей формулы:
Для наглядности: вы не заботитесь о последовательности состояний, которые рынок принимал, чтобы стать «бычьим». Вероятность того, что следующее состояние будет «медвежьим», определяется только тем фактом, что рынок в настоящее время находится в «бычьем» состоянии. Это также имеет смысл на практике.
Процесс, обладающий Марковским свойством, называется Марковским процессом. Из-за чего же важна Марковская цепь? Из-за своего стационарного распределения.
Что такое стационарное распределение
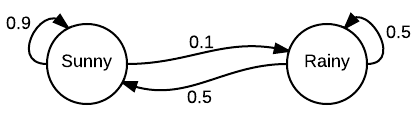
Я попытаюсь объяснить стационарное распределение, рассчитав его для приведённого ниже примера. Предположим, у вас есть Марковский процесс для фондового рынка, как показано ниже.
У вас есть матрица переходных вероятностей, которая определяет вероятность перехода из состояния Xi в Xj.
В приведённой матрице переходных вероятностей Q вероятность того, что следующим состоянием будет «бык», учитывая текущее состояние «бык» = 0,9; вероятность того, что следующее состояние будет «медвежьим», если текущее состояние «бык» = 0,075. И так далее.
Что ж, давайте начнём с какого-то определённого состояния. Наше состояние будет задаваться вектором [бык, медведь, стагнация]. Если мы начнём с «медвежьего» состояния, вектор будет таким: [0,1,0]. Мы можем вычислить распределение вероятности для следующего состояния, умножив вектор текущего состояния на матрицу переходных вероятностей.
Заметьте, что вероятности дают в сумме 1.
Следующее распределение состояний можно найти по формуле:
И так далее. В конце концов, вы достигнете стационарного состояния, в котором состояние стабилизируется:
Вы можете получить стационарное распределение при помощи следующего кода:
Вы также можете начать с любого другого состояния — достигнете того же стационарного распределения. Измените начальное состояние в коде, если хотите в этом убедиться.
Теперь мы можем ответить на вопрос, почему же стационарное распределение так важно.
Стационарное распределение важно, потому что с его помощью можно определять вероятность системы быть в определенном состоянии в случайное время.
Для нашего примера можно сказать, что в 62,5% случаев рынок будет в «бычьем» состоянии, 31,25% — в «медвежьем» и 6,25% — в стагнации.
Интуитивно вы можете рассматривать это как случайное блуждание по цепи.
Вы находитесь в определенной точке и выбираете следующее состояние, наблюдая распределение вероятностей следующего состояния с учётом текущего состояния. Мы можем посещать некоторые узлы чаще, чем другие, основываясь на вероятностях этих узлов.
Именно таким образом на заре интернета Google решил проблему поиска. Проблема заключалась в сортировке страниц, в зависимости от их важности. В Google решили задачу, используя алгоритм Pagerank. В алгоритме Google Pagerank следует рассматривать состояние как страницу, а вероятность страницы в стационарном распределении — как ее относительную значимость.
Теперь перейдём непосредственно к рассмотрению методов MCMC.
Что такое методы Монте-Карло с цепями Маркова (MCMC)
Прежде чем ответить, что же такое MCMC, позвольте задать один вопрос. Мы знаем о бета-распределении. Мы знаем его функцию плотности вероятностей. Но можем ли мы взять выборку из этого распределения? Вы можете придумать способ, как это сделать?
MCMC даёт возможность выбрать из любого распределения вероятностей. Это особенно важно, когда нужно сделать выборку из апостериорного распределения.
Например, нужно сделать сэмпл из апостериорного распределения. Но легко ли вычислить апостериорную компоненту вместе с нормирующей постоянной (evidence)? В большинстве случаев можно найти их в виде произведения правдоподобия и априорной вероятности. Но рассчитать нормирующую постоянную (p (D)) не получится. Почему? Разберёмся подробнее.
Предположим, H принимает только 3 значения:
p(D) = p(H=H1).p(D|H=H1) + p(H=H2).p(D|H=H2) + p(H=H3).p(D|H=H3)
В таком случае p(D) подсчитать легко. А что, если значение H непрерывно? Получилось бы ли рассчитать это так же легко, особенно если H принимала бесконечные значения? Для этого пришлось бы решить сложный интеграл.
Мы хотим сделать случайный отбор из апостериорного распределения, но также хотим считать p(D) константой.
Методы Монте-Карло с цепями Маркова — это класс алгоритмов для выборки из распределения вероятностей, основанный на построении цепи Маркова, которая в качестве стационарного распределения имеет желаемый вид. Состояние цепи после ряда шагов затем используется в качестве выборки из желаемого распределения. Качество выборки улучшается с увеличением количества шагов.
Разберёмся на примере. Допустим, нужна выборка из бета-распределения. Его плотность:
где C — нормирующая постоянная. На самом деле это некоторая функция от α и β, но я хочу показать, что для выборки из бета-распределения она не нужна, поэтому мы примем ее за константу.
Задача с бета-распределением действительно сложная, если не сказать практически неразрешимая.
В действительности вам, вероятно, придётся работать с более сложными функциями распределения, а иногда вы не будете знать нормирующие постоянные.
Методы MCMC облегчают жизнь, предоставляя алгоритмы, которые могли бы создать цепь Маркова, которая в качестве стационарного распределения имеет бета-распределение, учитывая, что мы можем выбирать из равномерного распределения (что относительно просто).
Если начнём со случайного состояния и перейдём к следующему состоянию на основе некоторого алгоритма несколько раз, мы в конечном итоге создадим цепь Маркова, у которой в качестве стационарного распределения будет бета-распределение. А состояния, в которых мы окажемся через долгое время, могут использоваться как выборка из бета-распределения.
Один из таких MCMC-алгоритмов — алгоритм Метрополиса-Гастингса.
Алгоритм Метрополиса-Гастингса
Интуиция:
Интуитивно понятно, что мы хотим ходить по некоторой кусочной поверхности (нашей цепи Маркова) таким образом, чтобы количество времени, которое мы проводим в каждом местоположении, было пропорционально высоте поверхности в этом месте (желаемая плотность вероятности, из которой хотим сделать выборку).
Так, например, мы хотели бы провести вдвое больше времени на вершине холма высотой 100 метров, чем на соседнем 50-метровом холме. Хорошо, что мы можем сделать это, даже если не знаем абсолютных высот точек на поверхности: все, что нужно знать, это относительные высоты. Например, если вершина холма A в два раза выше вершины холма B, то мы бы хотели провести в A вдвое больше времени, чем на B.
Существуют более сложные схемы предложения новых мест и правил их принятия, но основная идея заключается в следующем:
Цель MCMC — выборка из некоторого распределения вероятностей без необходимости знать его точную высоту в любой точке (не нужно знать C).
Если процесс «блуждания» настроен правильно, вы можете убедиться, что эта пропорциональность (между проведенным временем и высотой распределения) достигнута.
Алгоритм:
Теперь давайте определим и опишем поставленную задачу более формально. Пусть s = (s1, s2,…, sM) — желаемое стационарное распределение. Мы хотим создать цепь Маркова с таким стационарным распределением. Начнем с произвольной цепи Маркова с M-состояниями с матрицей перехода P, так, что pij представляет вероятность перехода из состояния i в j.
Интуитивно мы знаем, как бродить по цепи Маркова, но цепь Маркова не имеет требуемого стационарного распределения. Эта цепь имеет некоторое стационарное распределение (которое нам не нужно). Наша цель — изменить способ, которым мы блуждаем по цепи Маркова, чтобы цепь имела желаемое стационарное распределение.
После большого количества испытаний эта цепь будет сходиться и иметь стационарное распределение s. Затем мы можем использовать состояния цепи как выборку из любого распределения.
Проделывая это для выборки бета-распределения, единственный раз, когда приходится использовать плотность вероятности, — это поиск вероятности принятия решения. Для этого делим sj на si (то есть нормирующая постоянная C сокращается).
Выборка из бета-распределения
Теперь перейдём к проблеме выборки из бета-распределения.
Бета-распределение — непрерывное распределение на [0,1] и может иметь бесконечные значения на [0,1]. Предположим, что произвольная цепь Маркова P с бесконечными состояниями на [0,1] имеет переходную матрицу P такую, что pij = pji = все элементы в матрице.
Нам не нужна Матрица P, как мы увидим позже, но я хочу, чтобы описание проблемы было максимально приближено к алгоритму, который мы предложили.
Цепь Маркова – это просто: подробно разбираем принцип
Цепь Маркова – череда событий, в которой каждое последующее событие зависит от предыдущего. В статье мы подробнее разберём это понятие.
Цепь Маркова – это распространенный и довольно простой способ моделирования случайных событий. Используется в самых разных областях, начиная генерацией текста и заканчивая финансовым моделированием. Самым известным примером является SubredditSimulator. В данном случае Цепь Маркова используется для автоматизации создания контента во всем subreddit.
Цепь Маркова понятна и проста в использовании, т. к. она может быть реализована без использования каких-либо статистических или математических концепций. Цепь Маркова идеально подходит для изучения вероятностного моделирования и Data Science.
Сценарий
Представьте, что существует только два погодных условия: может быть либо солнечно, либо пасмурно. Всегда можно безошибочно определить погоду в текущий момент. Гарантированно будет ясно или облачно.
Теперь вам захотелось научиться предсказывать погоду на завтрашний день. Интуитивно вы понимаете, что погода не может кардинально поменяться за один день. На это влияет множество факторов. Завтрашняя погода напрямую зависит от текущей и т. д. Таким образом, для того чтобы предсказывать погоду, вы на протяжении нескольких лет собираете данные и приходите к выводу, что после пасмурного дня вероятность солнечного равна 0,25. Логично предположить, что вероятность двух пасмурных дней подряд равна 0,75, так как мы имеем всего два возможных погодных условия.
Теперь вы можете прогнозировать погоду на несколько дней вперед, основываясь на текущей погоде.
Этот пример показывает ключевые понятия цепи Маркова. Цепь Маркова состоит из набора переходов, которые определяются распределением вероятностей, которые в свою очередь удовлетворяют Марковскому свойству.
Обратите внимание, что в примере распределение вероятностей зависит только от переходов с текущего дня на следующий. Это уникальное свойство Марковского процесса – он делает это без использования памяти. Как правило, такой подход не способен создать последовательность, в которой бы наблюдалась какая-либо тенденция. Например, в то время как цепь Маркова способна сымитировать стиль письма, основанный на частоте использования какого-то слова, она не способна создать тексты с глубоким смыслом, так как она может работать только с большими текстами. Именно поэтому цепь Маркова не может производить контент, зависящий от контекста.
Модель
Формально, цепь Маркова – это вероятностный автомат. Распределение вероятностей переходов обычно представляется в виде матрицы. Если цепь Маркова имеет N возможных состояний, то матрица будет иметь вид N x N, в которой запись (I, J) будет являться вероятностью перехода из состояния I в состояние J. Кроме того, такая матрица должна быть стохастической, то есть строки или столбцы в сумме должны давать единицу. В такой матрице каждая строка будет иметь собственное распределение вероятностей.
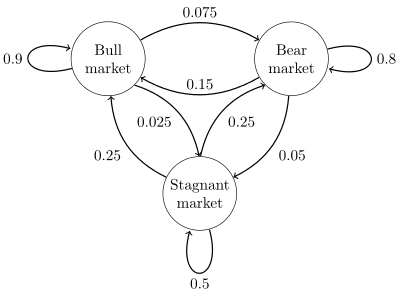
Общий вид цепи Маркова с состояниями в виде окружностей и ребрами в виде переходов.
Примерная матрица перехода с тремя возможными состояниями.
Цепь Маркова имеет начальный вектор состояния, представленный в виде матрицы N x 1. Он описывает распределения вероятностей начала в каждом из N возможных состояний. Запись I описывает вероятность начала цепи в состоянии I.
Этих двух структур вполне хватит для представления цепи Маркова.
Мы уже обсудили, как получить вероятность перехода из одного состояния в другое, но что насчет получения этой вероятности за несколько шагов? Для этого нам необходимо определить вероятность перехода из состояния I в состояние J за M шагов. На самом деле это очень просто. Матрицу перехода P можно определить вычислением (I, J) с помощью возведения P в степень M. Для малых значений M это можно делать вручную, с помощью повторного умножения. Но для больших значений M, если вы знакомы с линейной алгеброй, более эффективным способом возведения матрицы в степень будет сначала диагонализировать эту матрицу.
Цепь Маркова: заключение
Теперь, зная, что из себя представляет цепь Маркова, вы можете легко реализовать её на одном из языков программирования. Простые цепи Маркова являются фундаментом для изучения более сложных методов моделирования.