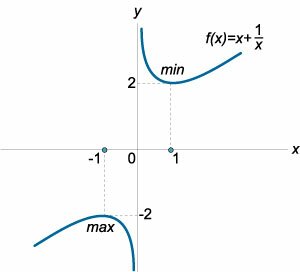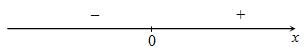что такое локальный максимум и минимум функции

Понятие экстремума функции

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Необходимое условие экстремума

(Необходимое условие экстремума)

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Первое достаточное условие экстремума

(Первое достаточное условие экстремума)

Решение. Находим производную заданной функции:

Второе достаточное условие экстремума

(Второе достаточное условие экстремума)

Понятие экстремума функции не по зубам? Тебе ответит эксперт через 10 минут!

Решение. Находим первую производную заданной функции:

Находим точки, в которых первая производная равна нулю:

Вторая производная заданной функции:

Остались вопросы?

Здесь вы найдете ответы.

Экстремум представляет собой значение функции на определенном интервале в момент достижения им минимального или максимального показания. Под понятием «экстремумы» или по-другому минимумы/максимумы подразумевается значение функции (у).

Если в определенной точке достигается экстремум или, иными словами, максимальное/минимальное значение функции на заданном интервале, то эта точка носит название точки экстремума. Из этого следует, что при достижении минимума, точка экстремума будет названа точкой минимума, и, наоборот, при достижении максимума эта точка будет называться точкой максимума. В случае, когда указываются точки экстремумов (или минимумов/максимумов) подразумеваются иксы, в которых достигаются минимальные или максимальные значения.

Под понятием «минимум функции» имеется в виду та точка на ней, в которой функция имеет значение, являющееся наименьшим среди всех значений, приобретаемых ею в любой из других соседних точек. Другими словами, это означает, что в случае, когда функция, достигнув определенной точки, прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и представляет собой точку ее минимума.

Для ответа на поставленный вопрос нужно отыскать точку минимума указанной функции, в которой ее значение перестает падать. Это можно сделать следующим образом:

Предположив, что минимальное значение данной функции равно 0, можно переписать равенство в следующем виде:

Сократим данное уравнение на 4:

Получившееся равенство также может быть записано в следующем виде после перемены местами слагаемых:

Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:

Это же уравнение может выглядеть так:

Теперь для упрощения можно переписать уравнение в таком виде:

В этом случае х = 1

Знаками «+» и «-» обозначены значения производной.

После проведенных вычислений было установлено, что х = 1, что является точкой минимума функции:

Точкой максимума называется то значение х, достигнув которого, производная начинает менять свой знак с плюса на минус. Зная это, можно перейти к поиску точки максимума для функции, указанной в задании.

Для этого нужно начать с поиска производной, используя следующую формулу:

Подставляем приведенные в задании значения и получаем:

Теперь следует приравнять производную к 0 и начать решать получившееся уравнение:

Упростим уравнение и получим:

Избавимся от минусов в уравнении:

Отсюда следует, что:

Можно сделать вывод о том, что х = 1,5.

Запишем производную данной функции:

А затем приравняем ее к 0:

Это позволяет сделать вывод о том, что:

Получается, что, если x 3/2, то производная y’ > 0, и в этом случае функция возрастает.

x =3/2=1,5 – это единственная точка экстремума, которая является точкой минимума.

Критическая точка функции представляет собой ту точку, при пересечении с которой производная данной функции становится равной 0, либо она вовсе не существует.

Для начала нужно определить, что под критической точкой функции подразумевается та точка, при пересечении с которой производная приобретает нулевое значение, либо же эта производная просто не существует в этой точке, что означает, что функцию в данной точке невозможно дифференцировать.

Проверим, применимо ли это утверждение к упомянутой в задании функции:

Приравняем производную функции к 0:

f ‘(x) = 0, это значит, что 2sin2x-3 = 0.

sin2x= 3 2 не имеет решения

Ответ: заданная функция не имеет критических точек и существует при любых х.

Под критическими точками функции понимаются те точки, в которых ее производная равна 0 или вовсе не существует.

Источник

Что такое локальный максимум и минимум функции

Точки, в которых производная функции \(f\left( x \right)\) равна нулю либо не существует, называются критическими точками данной функции. Следовательно, стационарные точки являются подмножеством множества критических точек.

Необходимое условие экстремума формулируется следующим образом:

Если точка \(\) является точкой экстремума функции \(f\left( x \right),\) то в этой точке либо производная равна нулю, либо не существует. Другими словами, экстремумы функции содержатся среди ее критических точек.

Отметим, что выполнение необходимого условия еще не гарантирует существование экстремума. Классической иллюстрацией здесь является кубическая функция \(f\left( x \right) = .\) Несмотря на то, что в точке \(x = 0\) производная данной функции равна нулю: \(f’\left( \right) = 0,\) эта точка не является экстремумом.

На основании определения заключаем, что точка \(\) является точкой строгого минимума функции \(f\left( x \right).\)

Аналогично можно доказать первое достаточное условие для строгого максимума функции.

Заметим, что в первом достаточном условии не требуется, чтобы функция была дифференцируемой в точке \(.\) Если в этой точке производная равна бесконечности или не существует (т.е. точка \(\) является критической, но не стационарной), то первое достаточное условие все равно можно использовать для исследования функции на максимум или минимум.

Аналогично рассматривается случай максимума.

Второй достаточный признак экстремума удобно применять, когда вычисление первых производных в окрестности стационарной точки затруднительно. С другой стороны, второй признак можно использовать лишь для стационарных точек (где первая производная равна нулю) − в отличие от первого признака, который применим к любым критическим точкам.

Ясно, что при \(n = 2\) в качестве частного случая мы получаем рассмотренное выше второе достаточное условие экстремума. Чтобы исключить такой переход, в третьем признаке полагают, что \(n > 2.\)

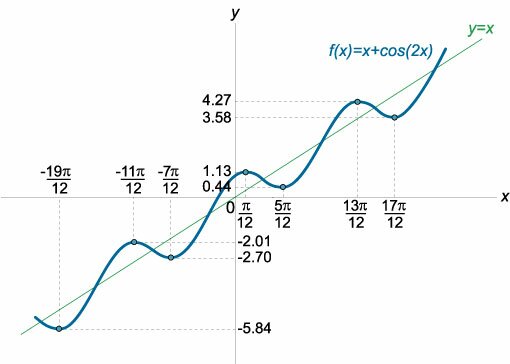
Данная функция относится к семейству показательно-степенных функций. В общем случае они имеют вид \(y = g<\left( x \right)^>.\) Обычно считают, что область определения показательно-степенных функций удовлетворяет условию \(g\left( x \right) > 0.\) (В некоторых частных случаях основание \(g\left( x \right)\) может быть отрицательным − например, если \(h = \large\frac<1><3>\normalsize.\) В нашем случае полагаем \(x > 0.\) Отсюда следует, что функция принимает лишь положительные значения.

\(2x = \large\frac<\pi ><6>\normalsize + 2\pi n,\;\; \Rightarrow = \large\frac<\pi ><<12>>\normalsize + \pi n,\;n \in \mathbb;\)

\(2x = \large\frac<5\pi ><6>\normalsize + 2\pi k,\;\; \Rightarrow = \large\frac<5\pi ><<12>>\normalsize + \pi k,\;k \in \mathbb.\)

Согласно принципу наименьшего действия Ферма, между любыми двумя точками реализуется такая траектория света, которая соответствует наименьшему времени распространения.

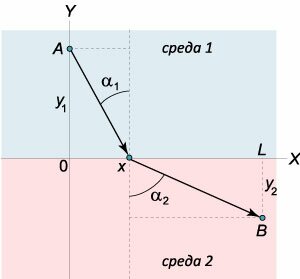
Рассмотрим две среды с плоской границей между ними (см. выше рисунок \(8\)). Пусть свет распространяется из точки \(A\) в точку \(B\), причем в первой среде угол падения (угол между падающим лучом и нормалью к границе раздела сред) составляет \(<\alpha _1>,\) а во второй среде угол выходит под углом \(<\alpha _2>.\) Скорости света в первой и второй среде равны, соответственно, \(\) и \(.\)

Пусть луч пересекает границу между средами в точке с координатой \(x\). Задача состоит в том, чтобы определить значение \(x,\) при котором время распространения света будет наименьшим.

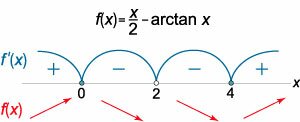
Исследуем изменение знака производной при переходе через эти точки (рисунок \(11\)).

Схематический вид данной функции приведен на рисунке \(12\).

\(\ln x = 0,\;\; \Rightarrow = 1;\)

Источник

Что такое локальный максимум и минимум функции

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом. Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Необходимое условие экстремума. Теорема.

. Запомните, что не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Первое достаточное условие экстремума. Теорема.

Пусть для функции \(f(x)\) выполнены следующие условия:

Тогда в точке \(x = \) функция \(f(x)\) имеет экстремум, причем это минимум, если при переходе через точку \(\) производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку \(\) производная меняет свой знак с плюса на минус.

Если производная \(f'(x)\) при переходе через точку \(\) не меняет знак, то экстремума в точке \(x = \) нет.

Таким образом, для того чтобы исследовать функцию \(f(x)\) на экстремум, необходимо:

Рассмотрим пример использования данного алгоритма, исследуем функцию на экстремумы: \(y(x) = — 1.\)

\(y'(x) = 4 = 0 \Rightarrow x = 0.\)

Первая производная определена во всех точках. Таким образом, имеем одну критическую точку. Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки. Для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины:

Так как при переходе через точку \(x = 0\) производная сменила свой знак с «-» на «+», то в этой точке функция достигает минимума (или минимального значения).

Важно, что \(x = 0\) является точкой минимума. Сам же экстремум, минимум функции или наименьшее значение функции необходимо еще посчитать, подставив \(x = 0\) в выражение функции:

Не забывайте данное замечание и всегда внимательно читайте условие, что именно необходимо записать в ответе к задаче.

Источник

Максимумы, минимумы и экстремумы функций

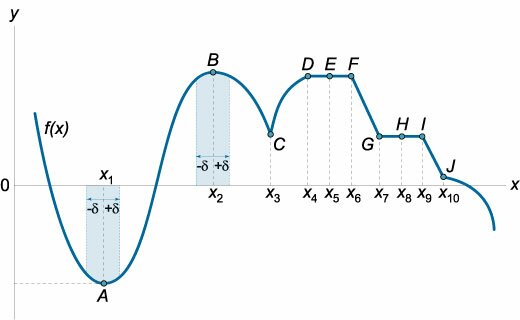
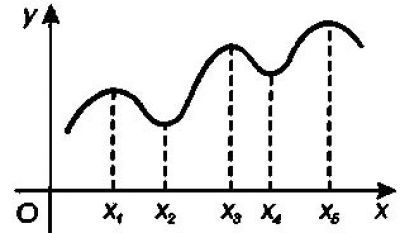
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.

\(- 9\): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является \(-2\).

Источник

Как найти точку максимума функции?

Глобальный и локальный максимум

Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.

Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:

Исследование

Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):

Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.

Область допустимых аргументов

Асимптоты

Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.

Производная и экстремумы

Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.

1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент «0», и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.

После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).

Концы интервала и сравнение результатов

При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.

Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.

Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.

Видео

Источник