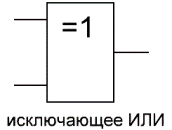что такое логический элемент вентиль
Архитектура компьютера. Цифровой логический уровень
Компьютер — это машина, которая может выполнять вычисления через исполнение примитивных операций. Она может понимать только два сигнала, которые принимаются за 0 и 1.
Организация архитектур машин представляется как ряд уровней, каждый из которых надстраивается над нижележащим уровнем. Это сделано не просто так, с помощью многоуровневой архитектуры мы можем абстрагироваться от реализации и сложности нижнего уровня, тем, самым облегчить процесс проектирования, и уменьшить вероятность ошибок. Абстрагирование является ключевым моментом во всей архитектуре компьютера.
Организация компьютера состоит из 6 уровней: цифровой логический, микроархитектура, архитектура набора команд (ISA), операционная система, язык ассемблера, прикладной, конечно, если не считать физический уровень, который находится ниже цифрового логического уровня. У меня нет пока что в планах рассказывать все, что происходит выше уровня ISA. На это есть две причины: во-первых, цель этих статей заключается не в том, чтобы рассмотреть все уровни, а в том, чтобы показать, что из себя представляют уровни 0-2, и, во-вторых, на habr’е существует немало статей по уровням выше ISA и без меня. В этой статье будет показан цифровой логический уровень, а в следующих двух микроархитектура и архитектура набора команд соответственно.
Цифровой логический уровень
Цифровой логический уровень по сути представляет собой набор логических функций, которые взаимодействую между собой для выполнения большей задачи. Вся работа этого уровня заключается в двух базовых концепциях: вентили и булева алгебра. Сначала я расскажу про них, а дальше про логические схемы и то как они используются при разработке, и в заключении, то что из себя представляет память и как она реализуется.
Вентиль
Вентиль (рис. 1.0) является устройством, которое принимает входные сигналы и выдает выходные, сам он реализован на транзисторах (об их работе я рассказывать не буду). Вентили используются на данном уровне как «строительный» материал, чтобы представлять базовые логические операции, а дальше уже идет их комбинирование для реализации тех или иных схем, то есть смысл данного уровня заключается в построении переиспользуемых схем, а не о работе вентилей (и транзисторов); дальше уже на основе этих схем могут быть построены более сложные и узкоспециализированные схемы, например, целые модули памяти, различная логика, например, для того как будут взаимодействовать компоненты CPU на уровне микроархитектуры и тд.
Рисунок 1.0. Изображение вентилей.
Таблица 1.0. Таблица истинности для основных операций.
| A | B | И | И-НЕ | ИЛИ | ИЛИ-НЕ | ИСК-ИЛИ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Булева алгебра
Этот вид алгебры работает с 0 и 1, здесь присутствуют такие операции (табл. 1.0) как: И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание), ИСКЛЮЧАЮЩЕЕ ИЛИ и их комбинации и т.д. Чтобы описать логические функции можно использовать разные способы, но мы сконцентрируемся только на двух: таблица истинности и дизъюнктивно нормальная форма.
Для построения таблицы истинности мы просто перебираем все комбинации значений всех переменных. Таблица позволяет увидеть нам все возможные комбинации при которых функция принимает значения истины или лжи, она подходит, когда нам необходимо такое свойтсво, например, декодер. Дизъюнктивно нормальная форма позволяет нам сократить ее размеры таблицы, для этого, мы используем только те комбинации значений переменных при которых функция принимает только истинные значения. Чтобы создать схему, которая будет принимать истинное значение только с нужными нам комбинациями, нам необходимо представить эти строки в виде минтерм.
Рисунок 1.1. Схема ИСКЛЮЧАЮЩЕГО ИЛИ (черта над переменной обозначает НЕ).
Логические схемы
Логическая схема — это набор объединенных вентилей с входными и выходными сигналами. На рис 1.1 тоже изображена схема у которой входными сигналами являются A и B, выходной сигнал идет от операции ИЛИ; также у нее есть три вентиля: два И, один ИЛИ. Теперь давайте рассмотрим некоторые виды схем с которыми нам потребуется встречаться в дальнейшем, к ним относятся: комбинационные, арифметические, интегральные схемы.
Комбинационные схемы
Комбинационная схема — это схема с одним дополнительным свойством: значения выходных сигналов зависят только от входных, или другими словами, в ней нет никаких запоминающих устройств. Из этого вида схем создаются переиспользуемые компоненты, которые применяются для реализации большинства других схем, мы рассмотрим несколько, а именно: компаратор, декодер, мультиплексор/демультиплексор.
Компаратор имеет n входных парных линий (то есть 2n входов) и одну выходную линию. Логика его работы заключается в том, чтобы сравнить каждую пару битов (биты слова A сравниваются с соответствующими битами слова B) и при неравенстве хоть одной из них выдать 0 (если за ложь принят 0), иначе 1. Давайте построим таблицу истинности (табл. 1.1) для однобитного компаратора; можно заметить, что она равна таблице истинности ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ (когда к операции добавлен НЕ, то все выходные значения в таблице становятся противоположными). Теперь давайте расширим его до двухбитного компаратора, построим таблицу истинности (табл. 1.2) для него от двух переменных значения которых зависит от двух однобитных компаратора, то есть от двух ИСКЛЮЧАЮЩЕГО ИЛИ-НЕ; в ней значение 1 в CMP0 (и CMP1) значит, что два входа какото-то компаратора равны, 0 наоборот, то есть 1 в столбце R должна быть только, когда значения равны в двух компараторах. Эта таблица истинности совпадает с таблицей И, то есть мы объединяем все ИСКЛЮЧАЮЩЕГО ИЛИ-НЕ операцией И и у нас получится двухбитный компаратор (рис. 1.3а). Для дальнейшего расширение компаратора необходимо лишь добавить ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ и подсоединить его к И. Недостаток такой реализации заключается в ее избыточности, нам требуется добавлять вентили НЕ для каждого ИСКЛЮЧАЮЩЕГО ИЛИ; мы можем от этого избавится (рис. 1.3б), если заменим вентиль И с НЕ входами на ИЛИ-НЕ, так как их таблицы истинности совпадают.
Таблица. 1.1. Таблица истинности для однобитного компаратора.
Рисунок 1.3. Две схемы двухбитных компараторов.
Декодер обладает n входными линиями, 2^n выходными, он реализован так, чтобы сигнал (истинна, 1) прошел только в одну выходную линию. Каждый выходной вентиль И получает свою комбинацию значений переменных, которые (значения) находятся в какой-то строке таблицы истинности, а как мы уже знаем, строку таблицы истинности можно реализовать как минтерму, то есть мы каждую строку представляем как вентиль И (рис. 1.4) от нескольких переменных. Основное применение декодера заключается в выборочном включении разных частей схемы (или схем), например, у АЛУ (о нем далее) имеется несколько операции, которые он может выполнять над входными значениями, чтобы их выбрать одну из них используется декодер.
Рисунок 1.4 Декодер.
Мультиплексор обладает 2^n входными линиями, n линиями управления и одной выходной линией. Он в реализации в какой-то степени похож (рис 1.5) на декодер, если представить входы декодера как линии управления, дополнить каждый вентиль И дополнительным входным сигналом и объединить выходные значения всех И одним ИЛИ. Суть его работы заключается в том, чтобы на выход поступал сигнал только от одной из возможных входных линий. Мультиплексор применяется в разных целях, например, он может пригодиться для преобразования параллельного кода в последовательный. Допустим у нас есть параллельная (это значит, что линии работают одновременно) шина с несколькими линиями по которым параллельно передаются биты; чтобы считать нужное нам слово (обычно разрядность слова соответствует разрядности регистра в процессоре) мы соединяем линий шины с входами мультиплексора и последовательно включаем по одному входу, допустим сверху вниз, тем самым на выход у нас пойдет точная последовательность битов.
Демультиплексор является обратным мультиплексору, он имеет одну входную линию, n линий управления и 2^n выходных линий. Логика его работы точно такая же как и в мультиплексоре, только один входной сигнал идет в один из выходных. Может быть использован для преобразования последовательного кода в параллельный.
Рисунок 1.5. Мультиплексор.
Арифметические схема
Данный вид схем выполняет арифметические операции над входными сигналами. Основными схемами являются: логические функции, сумматор, схема сдвига, АЛУ (ALU, Arithmetic Logic Unit).
Полусумматор и полный сумматор
Полусумматор состоит из двух входных и двух выходных линий, Полусумматор является простой схемой (рис. 1.6) из двух вентилей: И и ИСКЛЮЧАЮЩЕЕ ИЛИ. Сам по себе полусумматор может складывать только одноразрядные значения, но зачем же тогда нам нужен полный сумматор? В основном мы хотим складывать значения с большей разрядностью, но только одним полусумматором мы удовлетворить это желание не может. Когда мы складываем два одноразрядных значения, то у нас может произойти переполнение (табл. 1.3 последняя строка истинности в столбике перенос). Это когда результат операции не помещается в той разрядности, которой обладают входные элементы (в данном случае 1). При сложении двух единиц получает двойка, которую нельзя сохранить в одном бите, поэтому необходимо перенести его, чтобы воспользоваться при дальнейших вычислениях, но так как в полусумматоре не предусмотрена возможность использования двух значений и переноса одновременно, то складывать значения с разрядностью более чем единицу не получится. Например, допустим мы складываем два 3-разрядных числа, 5 (101 в двоичной) и 7 (111 в двоичной), сложение двух чисел начинается с младших разрядов, на входы полусумматора направляются 1 и 1, на выходе суммы получаем 0 и на выходе переноса 1, вот здесь и возникает проблема, следующие значения, которые должны пойти в полусумматор, это 0 и 1 соответственно, но, что делать с переносом, ведь для него нет никакого свободного входа, а отброс ить его нельзя, поэтому полусумматоры не могут напрямую использоваться для сложений.
У полного сумматора есть (рис. 1.7) три входных линии и две выходные линии. Входной перенос, как и выходной, используется для возможности объединения сумматоров в один с большей разрядностью. Сумматор состоит из двух полусумматоров, чтобы построить сумматор большей разрядности, необходимо только объединить сумматоры через входные и выходные переносы.
Рисунок 1.6. Схема полусумматор.
Таблица 1.3. Таблица истинности полусумматора.
Рисунок 1.7. Схема полного сумматора.
Таблица 1.4. Таблица истинности полного сумматора.
| A | B | Вход перенос | Сумма | Выход перенос |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Сдвиг необходим для того, чтобы, например, выполнять умножение (сдвиг влево) и деление (сдвиг вправо), но только с числами, которые являются степенью двойки (1, 2, 4, 8 и тд). Схема сдвига (рис. 1.8) должна выполнять смещение на одну позицию влево или вправо в зависимости от бита направления. Бит направления (С) в зависимости от своего значения включает те или иные вентили И. Если он равен 0 (сдвиг влево), то сигнал который идет напрямую (то есть не проходит через НЕ) будет выключать вентиль который находятся выше в паре из двух вентилей И и один крайний вентиль И снизу. Сигнал, который проходит через НЕ, будет включать нижние вентиль в паре из двух вентилей И и один крайний вентиль И сверху. Это значит, что входные значения In будут выходить только из вентилей И выходные сигналы, которых направлены в нижнюю сторону; старший бит (I3) будет утерян, так как самый нижний вентиль И не пропустит входной сигнал дальше. Аналогичная ситуация происходит, когда бит направления равен 1 (сдвиг вправо), только теперь будут включены другие вентили И и сигнал уже будет направлен в противоположную (в данной реализации) сторону, и, следовательно, произойдет сдвиг вправо.
Рисунок 1.8. Схема сдвига.
Арифметико Логическое Устройство
АЛУ — это схема (рис. 1.9), которая содержит в себе множество арифметических схем, она предназначена для того, чтобы в одном месте хранить все операции необходимые для какой-либо цели. Реализация АЛУ разделяется на несколько частей (в данной реализации): распространение входных операндов, логические функции, сумматор и мультиплексор. Как мы помним декодер должен выполнять«включение» операций, но здесь я решил сделать мультиплексор, который подает на выход «Результат» значение, только одной из четырех операций; два нижних вентиля И в нем делят одну и ту же комбинацию при которой мультиплексор работает, это необходимо потому, что «Выход переноса» и «Сумма» сумматора являются частью одной операции, то есть оба этих входа должны работать только когда выбрано суммирование. Наш АЛУ предназначен для работы с одноразрядными значениями, но его можно почти без проблем изменить на большую разрядность. Входные линии INA и INB предназначены для включения/выключения A и B соответственно.
Рисунок 1.9. Схема АЛУ.
Интегральные схемы
Также известна как микросхема, это те же схемы показанные выше, только они помещены в корпус, который определяет, то где должны находится выводы для сигналов. Этот вид схем возник из-за того, что продавать отдельные схемы и вентили не очень целесообразно: по крайне мере из-за того, что нет стандарта, который бы говорил как, где и в каком кол-ве должны располагаться входные и выходные сигналы.
Есть куча разных видов корпусов, но мы рассмотрим наиболее известные:
Память
У памяти выходные значения зависят не только от входных, то есть она способна запоминать. Концептуально все схемы памяти похожи (рис. 2.1), память может «запоминать» благодаря тому, что она «замкнута», то есть верхний вентиль зависит от выходного значения нижнего, а нижний зависит от выходного значения верхнего.
Рисунок 2.1. SR защелка.
Таблица 1.6. Таблица истинности SR защелки.
Когда мы подаем на входы S, R сигналы 0, а в Q хранится значение 0, то в верхний вентиль ИЛИ НЕ поступают два нуля 0, на выходе у него будет 1 (табл. 1.0). Далее в нижний вентиль ИЛИ-НЕ поступают 0 и 1, на выходе будет 0; то есть у нас получилось не противоречивое состояние защелки (рис. 2.2a). В данном случае выходное значение защелки равно 0 (Q), то есть она хранит значение 0.
В ином варианте мы можем подать на входы S, R сигналы 0, а в Q хранится значение 1. В верхний вентиль ИЛИ-НЕ поступают 0 и 1, что на выходе дает 0. В нижний вентиль ИЛИ-НЕ поступают 0 и 0, на выходе будет 1; Снова мы попали в не противоречивое состояние защелки (рис. 2.2б). Выходное значение защелки равно 1.
Рисунок 2.2. Два возможных корректных состояния SR защелки.
Логический вентиль
Количество эквивалентов вентилей используется как мера логической сложности схемы.
содержание
технологии
история
Бинарная система была впервые математически точно описана Готфридом Вильгельмом Лейбницем (опубликована в 1705 году), при этом Лейбниц также объяснил, как принципы арифметики и логики могут быть объединены с помощью этой системы.
В 1891 году американец Алмон Строуджер подал заявку на патент на «устройство, содержащее схему переключателя логического затвора», но он не утвердился до 1920-х годов. В 1898 году изобретатель Никола Тесла начал архивировать и совершенствовать такие устройства и заставил использовать электронные лампы вместо реле. Ли Де Форест окончательно изменил принципиальную схему электронной лампы Флеминга в 1907 году, чтобы ее можно было использовать в качестве логического элемента И.
Американский математик Клод Элвуд Шеннон основал идеи Витгенштейна в 1937 году, когда применил булеву алгебру в оценке и проектировании электрических цепей.
Первый интегрированный логический вентиль был создан Джеком Килби в 1958 году и состоял примерно из десяти компонентов. Десять лет спустя Texas Instruments производила схемы на транзисторно-транзисторной логике (схемы TTL серии 74xx ) большими сериями. Они быстро стали основой промышленной автоматизации.
Текущие исследовательские проекты связаны с молекулярными логическими воротами.
Таблица истинности
Схема КВ
Типы логических ворот и символика
Логические вентили обозначаются символами схем, которые определены в соответствии с различными, более или менее параллельными стандартами.
<\ Displaystyle Y = <\ тильда >>



| А. | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
(НЕ И)

Y знак равно А. ∧ ¯ Б. <\ Displaystyle Y = A \; \; \! \! <\ overline <\ wedge>> \; \; \! \! B>
Y знак равно А. ∨ ¯ Б. <\ Displaystyle Y = A \; \; \! \! <\ overline <\ vee>> \; \; \! \! B>
Y знак равно А. ∨ _ ¯ Б. <\ Displaystyle Y = A \; \; \! \! <\ overline <\ underline <\ lor>>> \; \; \! \! B>
Немецкие символы (правая колонка) раньше были распространены на европейском континенте; В англоязычном мире американские символы (средняя колонка) были и остаются обычным явлением. Символы МЭК получили ограниченное признание во всем мире и (почти) полностью игнорируются в американской литературе.
Логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и их таблицы истинности
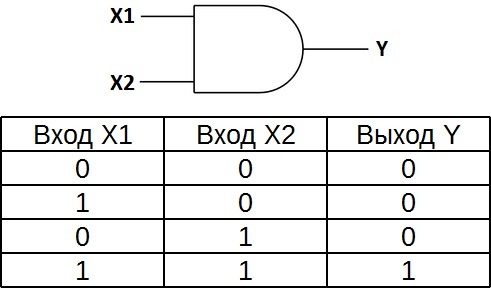
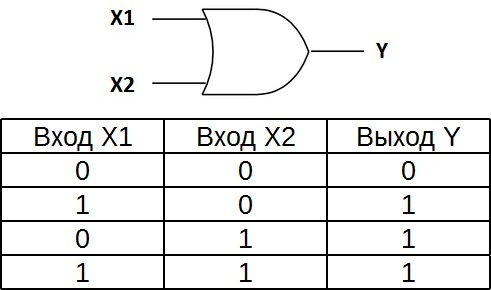
Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.
Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.
Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.
Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно.
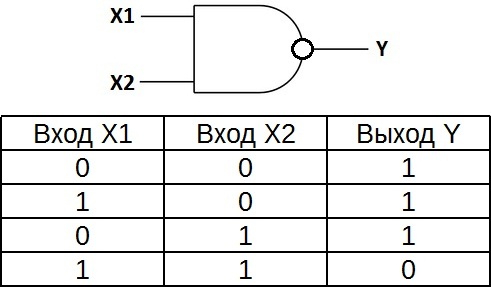
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль.
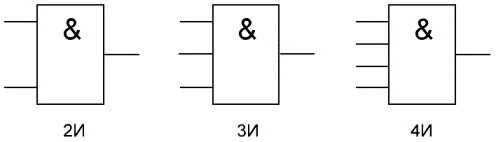
На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».
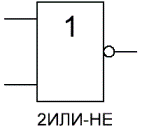
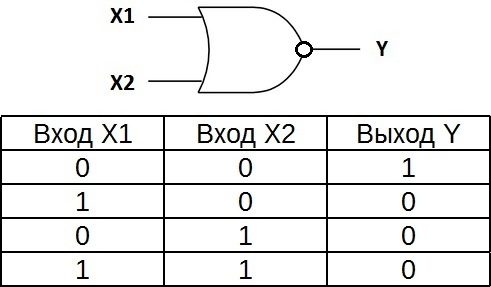
Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.
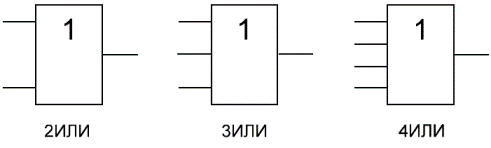
На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».
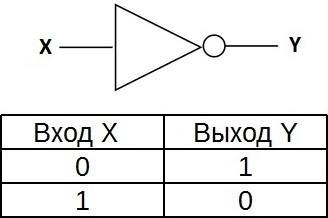
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.
На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.
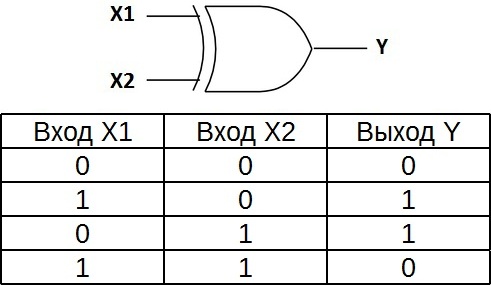
Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».
Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети: