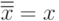что такое логическая функция
Логическая функция: что такое, способы представления, значение
Содержание:
Логическая функция — это такая функция, которая может принимать только одно из 2-х значений: 0 («ложь», «false») или 1 («истина», «true»). Логическую функцию можно обозначить как F (A), где А — это логический аргумент, чье количество в функции никак не ограничено.
Любая современная компьютерная система состоит из множества логических схем, где присутствуют логические функции и логические переменные. Для того чтобы описать эти взаимоотношения, есть таблицы истинности, в которых расписаны значения логической функции для разных наборов аргументов функции.
Логическая функция, что это
Логическая функция: отрицание
Логическая функция: конъюнкция
Логическая функция: дизъюнкция
Эта логическая функция, как и предыдущая, должна быть представлена несколькими аргументами. Ее значение буде «false» только в том случае, когда значения всех аргументов будет «false», во всех остальных случаях она будет «true».
Например нам даны два аргумента «А и В», тогда их таблица дизъюнкции будет выглядеть следующим образом:
Логическая функция: импликация
Логическая функция «импликация» — это такое выражение, которое показывает зависимость одного аргумента от другого. Его еще можно «прочитать» как «если А, то В». Обозначается как «А→В» и оно будет считаться «false» только тогда, когда А будет «true», а «В» будет «false».
Логическая функция: эквиваленция
Логическая функция «эквиваленция» простыми словами может читаться как «для А нужно и достаточно В». Его значение будет «true», только тогда, когда А и В вместе, либо «false», либо «true». Такая функция обозначается как «А↔В».
Вот как выглядит таблица истинности эквиваленции:
Логические функции
Урок 27. Информатика 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Логические функции»
· Для чего нужны логические функции в электронных таблицах?
· Какие задачи решают с помощью логических функций в электронных таблицах?
· Как пользоваться логическими функциями?
К логическим функциям относятся: ЕСЛИ, И, ИЛИ, НЕ. Результатом логического выражения является логическое значение ИСТИНА или логическое значение ЛОЖЬ.
В табличных процессорах логические функции записываются следующим образом: на первом месте записывают имя логической функции, далее в круглых скобках пишут логические операнды.
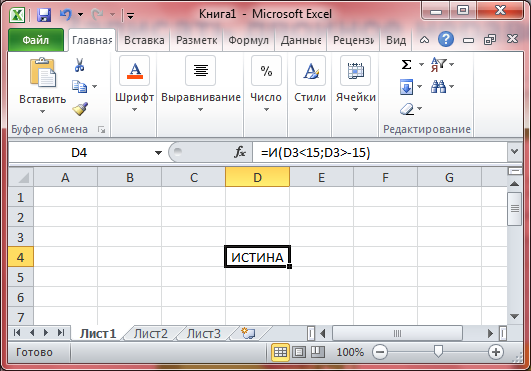
Логическая функция И в электронных таблицах будет записываться следующим образом:
=И (логическое значение 1; логическое значение 2)
Тогда наше логическое выражение будет выглядеть:
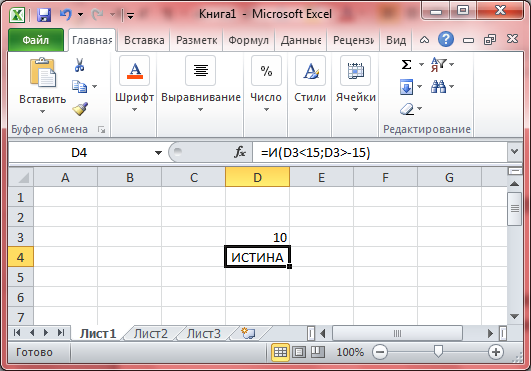
Обратите внимание! Если мы в ячейку D3 запишем, например, число 10, то наше выражение принимает значение ИСТИНА, так как число 10 входит в промежуток от –15 до 15.
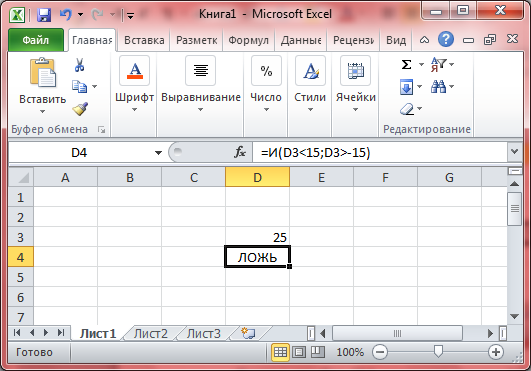
Если в ячейку D3 записать число 25, то выражение принимает значение ЛОЖЬ, так как число 25 в данный промежуток не входит.
Рассмотрим логическую функцию ЕСЛИ. Данная функция является одной из самых полезных, имеющихся в электронных таблицах. Функция ЕСЛИ проверяет, выполняется ли условие, и возвращает значение ИСТИНА, если оно выполняется, и значение ЛОЖЬ, если нет. Функцию ЕСЛИ ещё называют условной функцией.
В табличном процессоре условную функцию записывают следующим образом:
=ЕСЛИ (условие; [значение_если_истина]; [значение_если_ложь])
Рассмотрим решение следующей задачи:
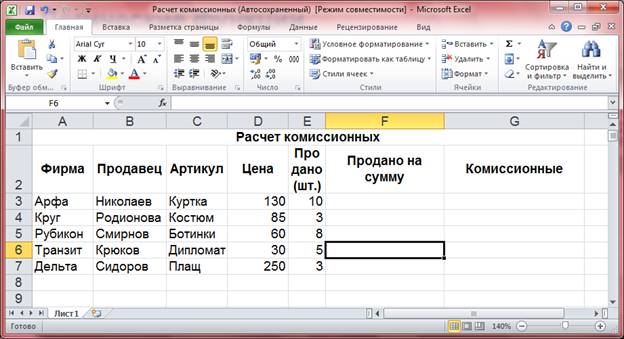
Некая торговая компания занимается реализацией непродовольственных товаров. На экране вы видите таблицу, в которой представлены результаты продаж за месяц. Давайте проставим каждому продавцу его процент комиссионных. Если продавец наторговал на сумму меньшую либо равную 400 условным единицам, то запишем ему в ячейку 5 %. Если же продано на сумму больше 400 условных единиц, то такому продавцу запишем 10 %.
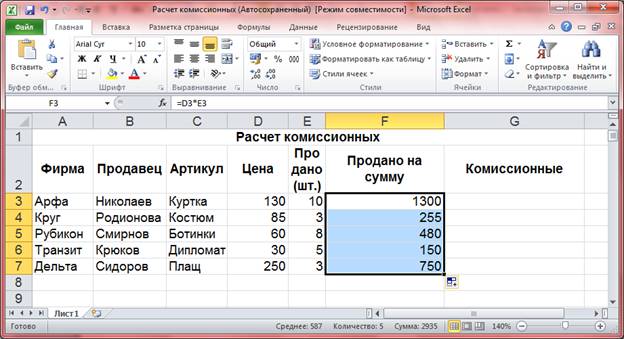
Перед нами таблица «Расчет комиссионных».
Сначала нам нужно рассчитать сумму, которую выручил каждый продавец от продаж товаров. Для этого в ячейку F3 запишем формулу: =D3*E3 и скопируем формулу в диапазон ячеек F4 F7.
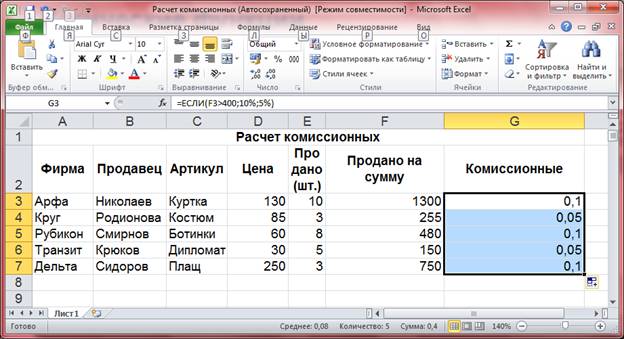
Теперь рассчитаем комиссионные для каждого продавца. В ячейку G3 запишем формулу, содержащую логическую функцию ЕСЛИ.
=ЕСЛИ(F3>400;10%;5%) и скопируем формулу в диапазон ячеек G4 G7.
Обратите внимание, мы не пользовались калькулятором, не делали никаких вычислений в уме, нам даже не пришлось сравнивать числа. Только с помощью табличного процессора и логических функций мы сделали необходимые вычисления.
Решим ещё одну задачу с использованием логической функции ЕСЛИ.
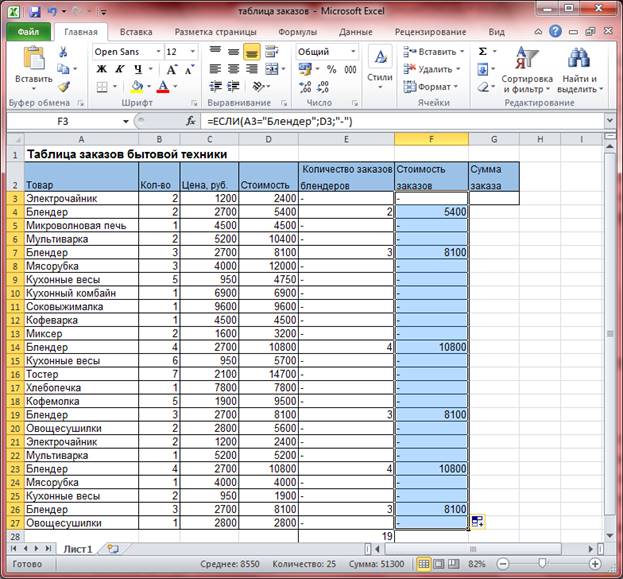
Интернет-компания занимается реализацией бытовой техники. Нужно по таблице заказов выяснить, сколько было заказано блендеров, а также рассчитать сумму заказа.
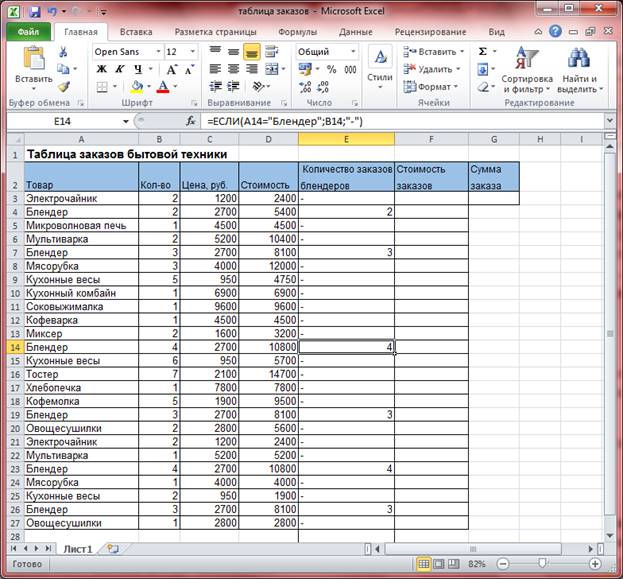
Итак, перед нами таблица заказов. Сначала найдем количество заказанных блендеров. Для этого:
В ячейку Е3 пишем формулу: =ЕСЛИ(A3=”Блендер”;B3;-). Нажимаем Enter. Здесь первый аргумент А3 = Блендер проверяет, содержится ли в ячейке А3 слово Блендер. Здесь проверяется символ за символ, и отличие даже одного символа в слове, в том числе и пробела, будет означать, что условие неверное. Если да, то в ячейку Е3 выводится В3, то есть количество, если нет, то в ячейке мы увидим прочерк. Скопируем формулу в диапазон ячеек Е4:Е27.
Формула содержит относительные ссылки, поэтому она автоматически изменилась. В столбце «Количество заказов блендеров» отобразились все «Количества» заказов.
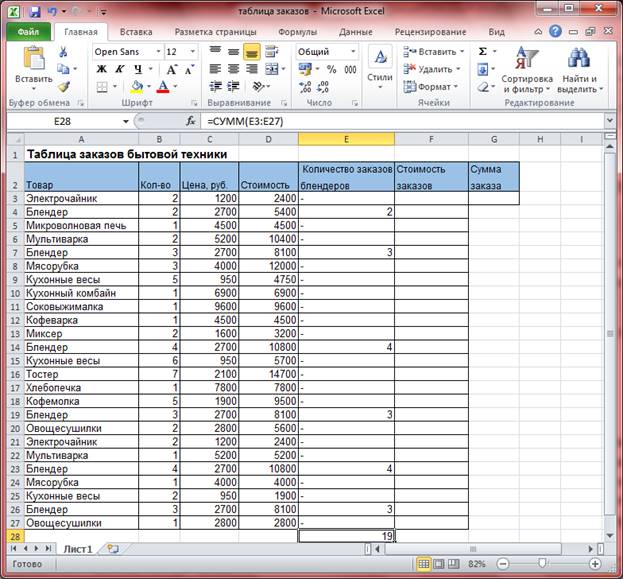
В ячейку Е28 запишем формулу: =СУММ(Е3:Е27), нажмем Enter и увидим, сколько блендеров было заказано.
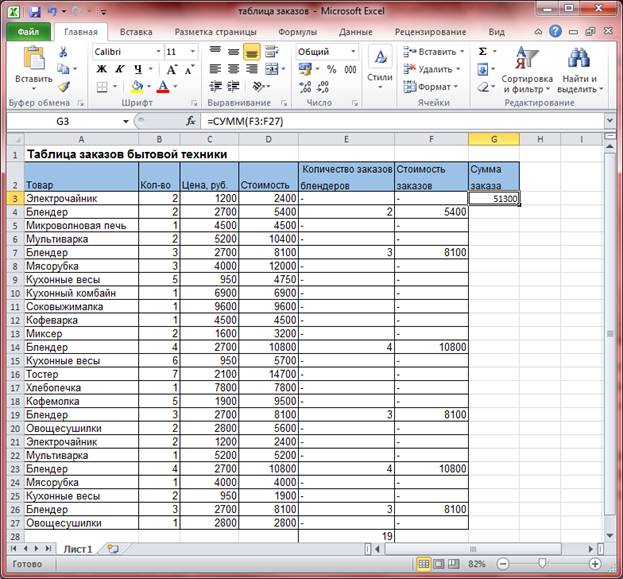
Теперь нужно найти сумму заказа. Для этого:
В ячейку F3 пишем формулу: =ЕСЛИ (A3=”Блендер”;D3;-). Нажимаем Enter. Здесь снова, первый аргумент А3 = Блендер проверяет, содержится ли в ячейке А3 слово Блендер. Если да, то в ячейку Е3 выводится D3, то есть стоимость, если нет, то в ячейке мы увидим прочерк. Скопируем формулу в диапазон ячеек F4:F27.
Формула содержит относительные ссылки, поэтому она автоматически изменилась. В столбце «Заказы блендеров» отобразились все «Стоимости» заказов. Теперь осталось только посчитать Сумму заказа. Для этого в ячейке G3 запишем формулу: =СУММ(F3:F27). Нажмём Enter.
Обратите внимание! Нам не пришлось самостоятельно искать строки с блендерами, выписывать стоимость товара и считать сумму заказа. Все необходимые поиски и вычисления за нас сделал табличный процессор с помощью логической функции ЕСЛИ.
Рассмотрим логическую функцию НЕ.
Принимает в виде аргумента всего одно логическое значение и меняет его на противоположное, т.е. значение ИСТИНА она изменит на ЛОЖЬ и наоборот, значение ЛОЖЬ на ИСТИНА.
В табличном процессоре логическую функцию НЕ записывают:
=НЕ (логическое значение)
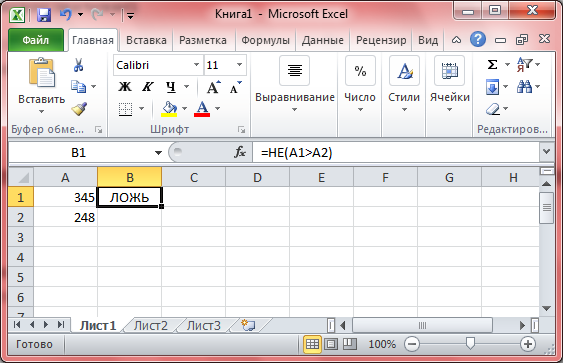
Например: в ячейке A1 записано число 345, а в ячейке A2 – число 248. В ячейке В1 записана формула: =НЕ(А1>А2). Данное выражение должно быть истинно, так как 345>248, но, применив функцию НЕ в формуле, мы изменили его на противоположное.
· К логическим функциям относятся: ЕСЛИ, И, ИЛИ, НЕ и другие.
· Результатом логического выражения является логическое значение ИСТИНА или логическое значение ЛОЖЬ.
· В табличных процессорах логические функции записываются следующим образом: на первом месте записывают имя логической функции, далее в круглых скобках пишут логические операнды.
Логические функции
Современная вычислительная техника строится на основе цифровых микросхем. При этом сами цифровые микросхемы реализуются на базе простейших логических функций:
Поэтому прежде чем приступить к изучению основ вычислительной техники рассмотрим особенности реализации логических функций на базе цифровых микросхем.
Логическая функция инвертирования
Простейшим логическим элементом является инвертор, который просто изменяет значение входного сигнала на прямо противоположное значение. Функция инвертирования входного сигнала, реализуемая цифровым инвертором, записывается в следующем виде:
где черта над входным значением цифрового сигнала обозначает изменение его на противоположное. То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 1. Так как входной параметр у логической функции инвертирования один, то ее таблица истинности состоит только из двух строк.
Таблица 1. Таблица истинности логической функции инвертирования
| In | Out |
|---|---|
| 0 | 1 |
| 1 | 0 |
В качестве логического инвертора можно использовать обычный транзисторный усилитель с транзистором, включенном по схеме с общим эмиттером или истоком. Схема, выполненная на биполярном n-p-n транзисторе, позволяющая реализовать функцию логического инвертирования приведена на рисунке 1.
Рисунок 1. Схема, позволяющая реализовать функцию логического инвертирования
Схемы логических инверторов могут обладать различным временем распространения цифрового сигнала и могут работать на различные виды нагрузки. Они могут быть выполнены на одном или на нескольких транзисторах, но независимо от схемы и её параметров они осуществляют одну и ту же логическую функцию. Для того, чтобы особенности включения транзисторов не затеняли выполняемую логическую функцию, были введены специальные обозначения для цифровых микросхем — условно-графические обозначения. Условно-графическое изображение логического инвертора приведено на рисунке 2.
Рисунок 2. Условно-графическое изображение логического инвертора
Логическая функция «И» (конъюнкция)
Следующей простейшей логической функцией, на основе которой реализуются элементы вычислительной техники является операция логического умножения «И». Логическая функция «И» обычно записывается следующим образом:
где символ ∧ обозначает функцию логического умножения. Эта же функция может быть записана несколькими способами:
То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 2. В формуле, приведенной выше, использовано два аргумента. Поэтому элемент, выполняющий эту функцию имеет два входа. Такая логическая функция обозначается «2И». Для нее таблица истинности будет состоять из четырех строк (2 2 = 4).
Таблица 2. Таблица истинности логической функции «2И»
| In1 | In2 | Out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Проще всего понять как работает логический элемент»2И», реализующий логическую функцию умножения, при помощи схемы, построенной на идеализированных ключах с электронным управлением, как это показано на рисунке 3. В этой схеме ток будет протекать только тогда, когда оба ключа будут замкнуты, следовательно, единичный уровень напряжения на выходе данной схемы появится только при двух логических единицах на входах идеализированных электронных ключей.
Рисунок 3. Принципиальная схема, реализующая логическую функцию «2И»
Условно-графическое изображение электронной схемы, выполняющей логическую функцию «2И», на принципиальных схемах цифровых и вычислительных устройств приведено на рисунке 4, и с этого момента схемы, выполняющие логическую функцию «И» будут приводиться именно в таком виде. Это изображение не зависит от конкретной принципиальной схемы устройства, реализующей функцию логического умножения.
Рисунок 4. Условно-графическое изображение схемы, выполняющей логическую функцию «2И»
Для закрепления материала рассмотрим логическую функцию «3И». Функция логического умножения трёх переменных записывается следующим образом:
Её таблица истинности будет содержать уже восемь строк (2 3 = 4). Таблица истинности трёхвходовой схемы логического умножения «3И» приведена в таблице 3, а ее условно-графическое изображение — на рисунке 5. В схеме же, построенной по принципу схемы, приведённой на рисунке 2, к цепочке последовательно соединенных электронных ключей придётся добавить третий ключ.
Таблица 3. Таблица истинности схемы, выполняющей логическую функцию «3И»
| In1 | In2 | In3 | Out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Условно-графическое изображение схемы, выполняющей логическую функцию «3И» приведено на рисунке 5.
Рисунок 5. Условно-графическое изображение схемы, выполняющей логическую функцию «3И»
Логическая функция «ИЛИ» (дизъюнкция)
Следующей функцией, широго использующейся при реализации вычислительных устройств является операция логического сложения «ИЛИ», которую часто называют дизъюнкцией. Эта операция двух выражений записывается следующим образом:
где символ ∨ обозначает функцию логического сложения. Иногда эта же логическая функция записывается в другом виде:
То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 4. В формуле, приведенной выше, использовано два аргумента. Поэтому схема, выполняющая функцию логического суммирования имеет два входа. Такой элемент обозначается «2ИЛИ». Для логической функции «2ИЛИ» таблица истинности будет состоять из четырех строк (2 2 = 4).
Таблица 4. Таблица истинности схемы, выполняющей логическую функцию «2ИЛИ»
| In1 | In2 | Out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Как и в случае, рассмотренном для схемы логического умножения, воспользуемся для реализации схемы «2ИЛИ» идеализированными электронными ключами. На этот раз соединим ключи параллельно. Схема, реализующая логическую функцию «2ИЛИ» (см. таблицу истинности 4), приведена на рисунке 5. Как видно из приведённой схемы уровень логической единицы появится на её выходе, как только будет замкнут любой из ключей, то есть схема реализует таблицу истинности, приведённую в таблице 4.
Рисунок 6. Принципиальная схема, реализующая логическую функцию «2ИЛИ»
Так как функция логического суммирования может быть реализована различными принципиальными схемами, то для обозначения этой функции на принципиальных схемах используется специальный символ ‘1’, как это показано на рисунке 7.
Рисунок 7. Условно-графическое изображение схемы, выполняющей логическую функцию «2ИЛИ»
Понравился материал? Поделись с друзьями!
Что такое логическая функция
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Основные понятия алгебры логики. Функции алгебры логики. Основные логические эквивалентности
Представление логической функции в виде таблицы истинности
Прежде всего, определимся с понятием «элементарная логическая функция». Чаще всего,это понятие в литературе никак не расшифровывается. В дальнейшем мы будем понимать под «элементарной логической функцией» ФАЛ от аргументов, каждый из которых, в свою очередь, не является логической функцией и которые имеют своё собственное обозначение.
Таблица истинности указывает значение логической функции при всех значениях наборов аргументов. Ниже мы рассмотрим элементарные логические функции от одной и двух переменных.
Все возможные элементарные логические функции от одной переменной представлены в Табл. 1.1:
| Функция | x | Наименование функции | Обозначение функции | |
|---|---|---|---|---|
| x=0 | x=1 | |||
| ƒ0 | 0 | 0 | Константа «ноль» | ƒ(x)=0 |
| ƒ1 | 0 | 1 | Тождественная функция | ƒ(x)=x |
| ƒ2 | 1 | 0 | Отрицание | 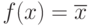 |
| ƒ3 | 1 | 1 | Константа «единица» | ƒ(x)=1 |
Здесь интерес представляет лишь одна функция – отрицание. Опишем ее основные свойства:
Последнее свойств можно описать как «отрицание отрицания есть утверждение».
Все возможные логические функции от двух переменных представлены в Табл. 1.2: