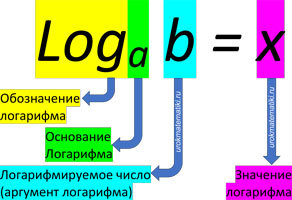
что такое логарифмы в математике

Логарифмы и их свойства

Обычно определение логарифма дают очень сложно и запутанно. Мы постараемся сделать это очень просто и наглядно.

Для того, чтобы разобраться, что такое логарифм, давайте рассмотрим пример:

Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.

Теперь при помощи этой таблицы введем понятие логарифма.

Логарифм от числа 32 по основанию 2 (\(log_<2>(32)\)) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:

Аналогично, глядя в таблицу получим, что:

Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.

Теперь дадим определение логарифма в общем виде:

Логарифмом положительного числа \(b\) по основанию положительно числа \(a\) называется степень \(c\), в которую нужно возвести число \(a\), чтобы получить \(b\)

Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:

Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:

Или логарифм шести по основанию 4:

На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!

Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм \(log_<4>(6)\). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6ке:

Значит \(log_<4>(6)\) принадлежите промежутку от 1 до 2:

Как посчитать логарифм

Почему так? Это следует из определения показательной функций. Показательная функция не может быть \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).

При этих ограничениях логарифм существует.

В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.

Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.

Теперь давайте разберем общий алгоритм вычисления логарифмов:

Давайте разберем на примерах.

Пример 1. Посчитать логарифм \(9\) по основанию \(3\): \(log_<3>(9)\)

Пример 2. Вычислить логарифм \(\frac<1><125>\) по основанию \(5\): \(log_<5>(\frac<1><125>)\)

Пример 3. Вычислить логарифм \(4\) по основанию \(64\): \(log_<64>(4)\)

Пример 4. Вычислить логарифм \(1\) по основанию \(8\): \(log_<8>(1)\)

Пример 5. Вычислить логарифм \(15\) по основанию \(5\): \(log_<5>(15)\)

Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\). Это довольно просто – нужно разложить \(a\) на простые множители.

\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.

Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) не будет степенью.

Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.

Десятичный логарифм

Натуральный логарифм

Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.

У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.

Свойства логарифмов

Давайте разберем несколько примеров на свойства логарифмов.

Пример 8. Воспользоваться формулой \(3\). Логарифм от произведения – это сумма логарифмов.

Пример 9. Воспользоваться формулой \(4\). Логарифм от частного – это разность логарифмов.

Пример 10. Формула \(5,6\). Свойства степени.

Логично, что будет выполняться и такое соотношение:

Пример 11. Формулы \(7,8\). Переход к другому основанию.

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок № 24. Логарифм. Свойства логарифмов.

Перечень вопросов, рассматриваемых в теме

1. Определение логарифма.

2. Основное логарифмическое тождество.

3. Свойства логарифмов.

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Логарифмирование – это действие нахождения логарифма числа.

Основное логарифмическое тождество:

Свойства логарифмов. При , справедливы равенства:

— логарифм произведения: ;

— логарифм частного: ;

— логарифм степени: .

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение имеет корень 5, т. к. значит , В уравнении число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.

Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.

Дадим определение логарифма.

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Т. е. логарифм числа по основанию , есть некоторое число такое, что .

, т. к. выполнены все условия определения:

1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) .

, т. к. выполнены все условия определения:

1) ; 2) 2 > 0, 2 ≠ 1; 3) .

Это действие называется логарифмированием.

Логарифмирование – это действие нахождения логарифма числа.

Существует краткая запись определения логарифма:

так называемое основное логарифмическое тождество. Его используют при вычислениях.

(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)

(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)

Решим несколько задач с использованием определения логарифма.

Задача 1. Вычислить .

Задача 2. Вычислить .

Решение. Для вычисления воспользуемся свойствами степеней: 1) , 2) и основным логарифмическим тождеством: .

.

Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.

1. Логарифм произведения.

Логарифм произведения чисел по основанию равен сумме логарифма по основанию и логарифма по основанию .

2. Логарифм частного.

Логарифм частного чисел по основанию равен разности логарифма по основанию и логарифма по основанию .

3. Логарифм степени.

Логарифм числа по основанию равен произведению показателя и логарифма по основанию .

Важно! Свойства выполняются при ,

Примеры и разбор решения заданий тренировочного модуля

№ 1. Вычислите: .

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

Представим в виде степени с рациональным показателем: . Далее воспользуемся свойством нахождения логарифма степени: . Вспоминаем таблицу квадратов: , значит , . Ответ: .

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

.

Источник

Формулы и свойства логарифмов

Определение логарифма

Логарифм — это математическая функция, основанная на свойствах возведения в степень.

Основываясь на математических формулах логарифмов, можно вычислить постоянную константу, которая в корреляции со всеми математическими константами окажет влияние на конечный результат логарифма числа. В месте с тем, этот результат приведет к трансформации объектов, равных пропорции необходимых логарифмов в пересчете на множители обратных функций.

С первого взгляда это сложно понять, но если увеличить коэффициент логарифма на равный ему множитель, то получится свойство логарифма применимое к школьной программе старших классов, а также для учащихся высших учебных заведений.

Категорическое решение логарифмов, основываясь на из свойствах, ставит в пропорцию их виды. Таким образом, формулы логарифмов соотносятся к самим логарифмам, как необходимая часть их самих.

Виды логарифмов

Для определения основания логарифма необходимо сначала определить его вид и, исходя из полученных результатов, по формуле и таблице сравнить корректность полученных значений. Это и будет основанием логарифма.

Чтобы решить логарифм необходимо понять, что a в степени x будет равно b, т.е. в какую степень x необходимо возвести основание логарифма a, чтобы получить значение b.

Примеры логарифмов:

В данных примерах можно увидель сложные и простые логарифмы, решение которых показывает, что всякий тождественный логарифм находится в пропорции его основания, за исключением вводных данных.

Конечно, основание логарифма пропорционально его значению, что приводит к равенству обратного значения. Это также необходимо учесть при рассмотрении равенства, кроме случаев, когда логарифм переностися с левой части равенства в правую.

log 2 8 = 3 (логарифм 8 по основанию 2 ), так как 2 3 = 8

log 7 49 = 2 (логарифм 49 по основанию 7 ), так как 7 2 = 49

Десятичный логарифм

Десятичный логарифм — логарифм по основанию 10.

Десятичный логарифм может быть не только как равенство степеней, но и показывать их различия. Наиболее хорошо это видно при разложении логарифма на члены в качестве констант a и b.

Конечным результатом решения десятичного логарифма является его сходство с натуральным логарифмом.

Примеры десятичных логарифмов:

lg 100 = 2 — десятичный логарифм обозначается именно так (lg), это десятичный логарифм ста;

Натуральный логарифм

При решении натурального логарифма его основа будет схожей с десятичным логарифмом за исключением того, что вместо числа 10 будет использоваться постоянная константа e.

Ещё одной особенностью натурального логарифма будет его неравенство по отношению к обратной функции.

Но стоит не приравнивать такое основание логарифма к прямой константе из-за большой разности при выборе метода подсчета логарифма.

Формулы и свойства логарифмов

Именно это свойство логарифмов позволяет вычислять точные значения в отличае от других методов вычисления.

Неточность других методов вычисления основывается на неверной корреляции остаточного члена логарифмического равенства.

Наряду с этим каждое из свойств является индивидуальным, равно как каждый из его членов. Всё это позволяет сделать вывод, что благодаря формулам, выведенным математиком, вычисления становятся простыми в рамках неравенств.

Основное логарифмическое тождество

Логарифм единицы

Вычисления такого логарифма применяются в балистике при расчете траектории движения объекта, находящегося в непосредственной близости от Земли. Это обусловлено наиболее точным значением ускорением свободного падения, равным 9,81. А при удалении от поверности Земли это значение изменяется, уменьшается пропорционально расстоянию удаления от поверхности.

Логарифм числа, равного основанию

Логарифмическая единица. Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.

Логарифм числа, обратного основанию

Логарифм произведения двух положительных чисел

Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2-х логарифмов, у которых будут одинаковые основания.

Логарифм частного

Логарифм частного. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.

Логарифм степени положительного числа

Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.

Логарифм корня числа

Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.

Основание логарифма в степени

Формула перехода к новому основанию

log a x = log b x log b a

log a x = 1 log x a

Производная логарифма

Производная логарифмической функции по основанию равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.

При расчёте производной логарифма необходимо учитывать ложный коэффициент производной, при котором нарастает его гиперболическая составляющая. Это и есть главное условие корректного нахождения производной логарифма. В то же время, нельзя упускать второстепенные составляющие при расчёте. К ним относятся расчеты с применением общей суммы логарифмов, а также пропорциональная составляющая двух вычисляемых логарифмов. Такой подход можно применить не только для вычисления производной натурального логарифма, но и при расчете производной десятичного логарифма при возведении в степень x по основанию a.

График логарифмов

Таким образом можно увидеть изменения логарифма по основанию от 0 до 10. Промежуточным результатом является логарифм по основанию e, которое приблизительно равно 2.72.

Так трафик логарифма по основанию 0 имеет форму прямой линии, а графики десятичного логарифма и натурального логарифма имею гиперболическую форму.

Источник