что такое логарифмический график в трейдинге
Логарифмический график
Хочу рассказать об одной важной вещи, которую должен знать каждый начинающий инвестор.
Сразу скажу, что когда я сам начинал инвестировать, я не знал об этом. Речь идет о логарифмическом графике, позволяющем объективно оценить долгосрочный рост активов.
Приведу определение логарифмического графика из Википедии:
«Логарифмический масштаб (шкала) — шкала, длина отрезка которой пропорциональна логарифму отношения величин, отмеченных на концах этого отрезка, в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах»
Если вы не учились на физ-мате, для вас это наверняка звучит как полная белиберда, собственно, как и для меня. Поэтому объясню своими словами.
Есть два вида графиков: линейный и логарифмический.
Первый вы все знаете: у него вертикальная шкала растет линейно, например, 0, 10, 20, 30, 40 и т.д. Т.е. шкалу задает величина между нулем и первым значением (абсолютный прирост в единицах, в примере – 10 единиц).
Со вторым интереснее: здесь рост нелинейный (геометрический), например, 0, 10, 20, 40, 80 и т.д. Тут шкалу задает относительный (процентный) прирост. В моем примере это рост в каждом периоде на 100%.
Разница в том, что логарифмический график более адекватно показывает относительный прирост. Т.е. в моем примере выше с логарифмическим графиком каждый год (пусть 0 — цена в первый год, 10 — во второй, 20 — в третий и т.д.) цена росла на 100%. И на графике это будет прямой трендовой линией.
Если этот же актив поместить на линейный график, то сначала будет казаться, что он почти не растет, а к концу мы увидим невероятный рост. Будет складываться ощущение, что актив перекуплен и вот-вот должен рухнуть.
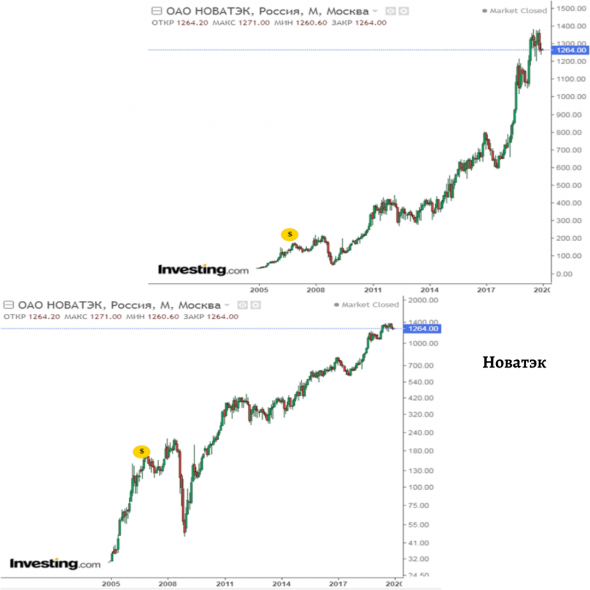
Чтобы наглядно это увидеть я привел несколько сравнений линейных и логарифмических графиков одних и тех же активов. Я взял данные по S&P 500, Татнефти и Новатэку и McDonald’s из Investing.com.
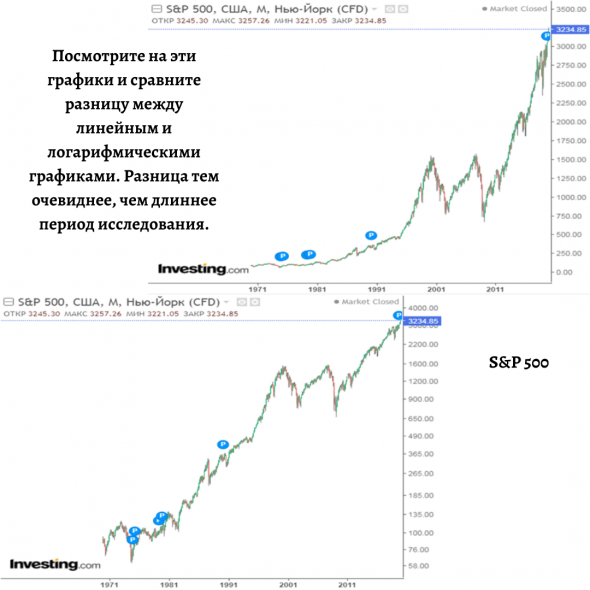
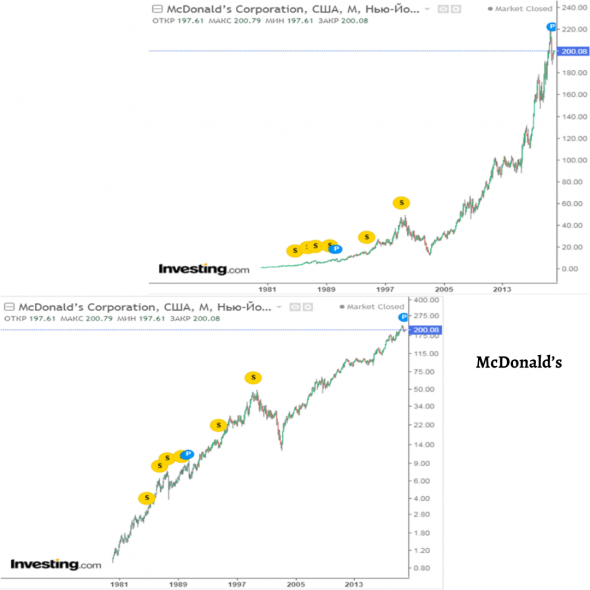
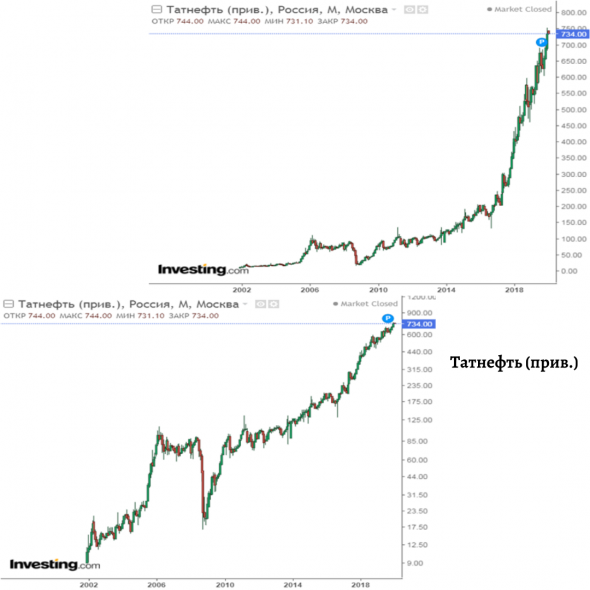
Если на графиках Татнефти и Новатэка эффект выражен не так сильно ввиду недолгого периода существования Московской биржи (хотя тоже существенен), то на американских графиках (S&P 500 и McDonald’s) разница очевидна. Посмотрите на McDonald’s: на линейном графике кажется, как будто люди с ума сошли: покупают невероятно выросший актив. В то же время складывается ощущение, что раньше McDonald’s вообще не рос и не представлял инвестиционной привлекательности (до 1990 года).
Если же посмотреть на логарифмический график McDonald’s, то мы увидим, что сейчас темп роста, наоборот, замедлился в процентном отношении. Именно этот график показывает правдивую картину. McDonald’s давно уже стал зрелой компанией, и он физически не может расти быстрее, потому что и так занимает огромную долю рынка. Он может только поддерживать стабильный, устойчивый рост.
Поэтому если вы придерживаетесь, что называется, long-term investments, т.е. долгосрочных инвестиций, то обязательно смотрите на логарифмический график, чтобы объективно оценить тренд и темпы роста цен на активы на длинных периодах времени.
Блог компании TradingView | Управление шкалой цен на платформе TradingView
Рассмотрев управление шкалой времени в предыдущем посте, теперь мы перейдем к рассмотрению управления шкалой цен на графиках платформы TradingView.
Настройки шкалы цен позволят установить отображение котировок на графиках согласно вашим предпочтениям.
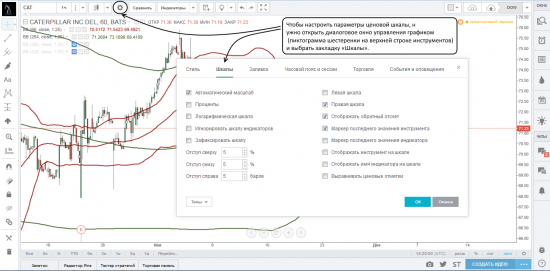
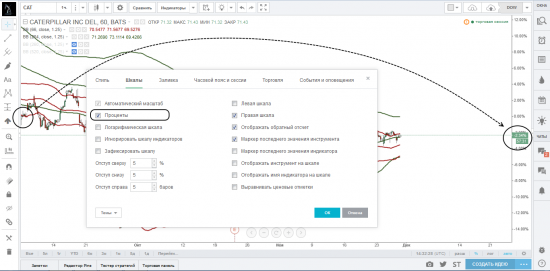
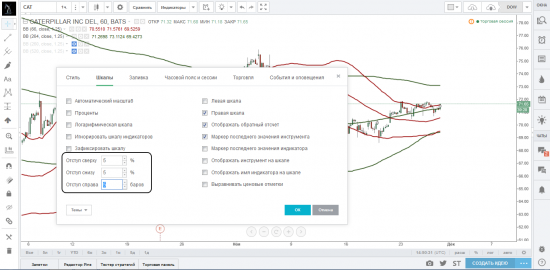
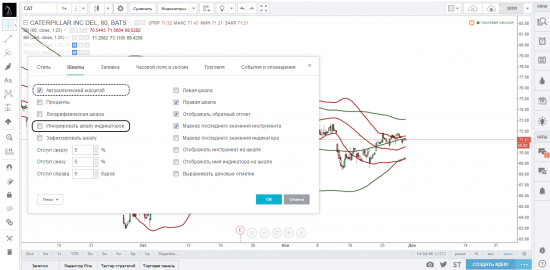
Чтобы настроить параметры ценовой шкалы, нужно открыть диалоговое окно управления графиком (пиктограмма шестеренки на верхней строке инструментов) и выбрать закладку «Шкалы».
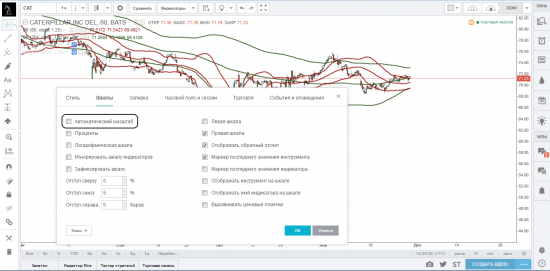
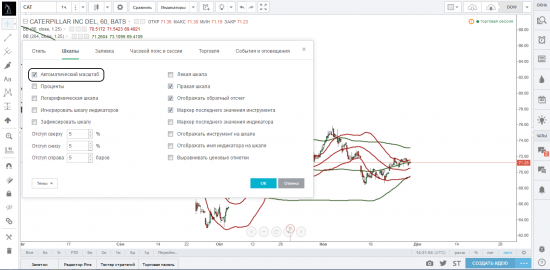
Поставив галочку напротив параметра «Автоматический масштаб», ваш график будет автоматически центрироваться с учетом представленных на нем инструментов и индикаторов. На картинках ниже мы представили график до и после выбора параметра «Автоматический масштаб».
Параметр «Проценты» позволяет представить шкалу цен в виде процентного соотношения относительно первой отображаемой цены на графике (первая цена от левого края). Этот параметр позволяет увидеть, на сколько процентов упала или выросла цена от начала наблюдаемого периода.
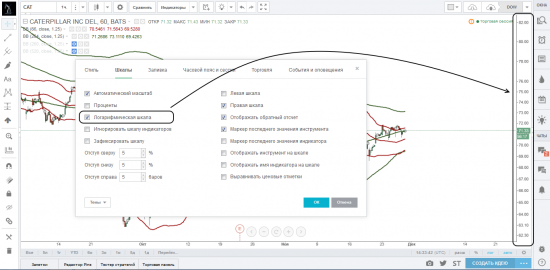
Параметр «Логарифмическая шкала» позволяет отобразить шкалу цен в виде логарифмической линейки.
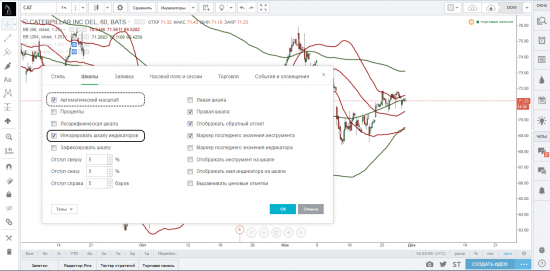
Параметр «Игнорировать шкалу индикаторов» работает только если включен параметр «Автоматический масштаб». При выборе данного параметра график будет центрироваться без учета нанесенных на него индикаторов. На картинках ниже мы представили график до и после выбора параметра «Игнорировать шкалу индикаторов» (с включенным параметром «Автоматический масштаб»).
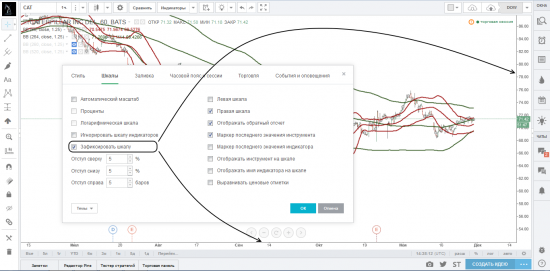
Поставив галочку напротив параметра «Зафиксировать шкалу», вы фиксируете масштаб временной и ценовой шкалы, что позволяет вам отдалять и приближать весь график без изменения его масштабов, просто колесиком мышки. На картинке представлен пример подобного отдаления.
Параметры отступа позволяют вам вручную выставить отступ графика сверху, снизу и сбоку. Данная функция может оказаться полезной при сравнении нескольких графиков, в которых отступ должен быть одинаков.
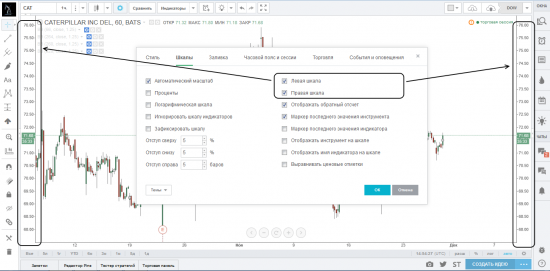
Параметры Левая и Правая шкала позволяют вам контролировать отображение левой и правой ценовой шкал, соответственно. Эта функция полезна при отображении двух и более инструментов на одном графике, цены которых значительно отличаются.
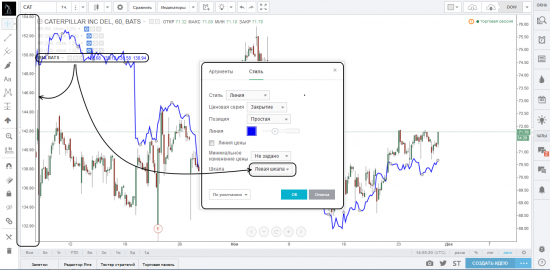
На картинках ниже мы показали пример отображения двух акций на одном графике (CAT по правой шкале и IBM по левой). На первой картинке мы включили левую шкалу, по умолчанию она отображает цену основного инструмента графика (CAT, то есть равна правой шкале). На второй картинке мы добавили сравниваемый инструмент (IBM) и настроили его отображение по левой шкале, на которой теперь отображается цена IBM.
В завершении нашего обзора мы рассмотрим параметры отображения инструментов на шкале цен.
Рыночные инварианты, или Зачем трейдеру логарифмы
Термином «инвариант» в науке принято обозначать величину остающуюся неизменной при тех или иных преобразованиях объекта. К примеру, внешность человека может очень сильно меняться под воздействием возраста, грима или пластической хирургии, но его всегда можно опознать по ДНК. Код ДНК является инвариантом – неизменной характеристикой. Инварианты часто несут наиболее важную информацию о том или ином предмете или явлении.Какое отношение все это имеет к финансовым рынкам? Финансовые рынки хорошо известны своей необычайной подвижностью. Цены большинства инструментов меняются, чуть ли не ежесекундно. Естественным образом возникает вопрос: есть ли что-то неизменное в этом море хаоса и нестабильности?
Цена учла все… и заблудилась
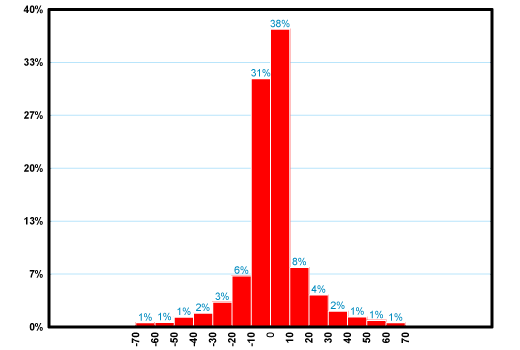
Известный постулат технического анализа гласит: «Цена учитывает все». Многие трейдеры поэтому важнейшей характеристикой фининструмента считают его цену. Можно ли признать цену рыночным инвариантом? Не смотря на всю экономическую важность понятия «цена», ответ на этот вопрос отрицательный. Цена постоянно меняется, значит, по определению она не может быть инвариантом. А что же средняя цена? Скользящие средние – один из наиболее популярных методов анализа. Возможно, средняя цена демонстрирует качество неизменности и устойчивости? Оказывается, нет. В этом можно наглядно убедиться из следующей картинки.
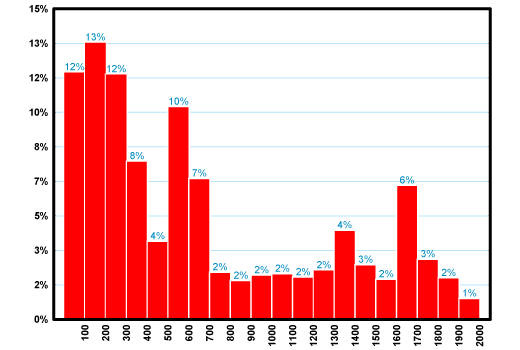
На ней представлена гистограмма дневных «цен» закрытия индекса ММВБ с 1998 по 2009 год. Значения индекса в этот период колебались от минимального 18.53 до максимального 1969.91. Средняя цена составляла 669.19. Гистограмма показывает процент попаданий наблюдаемой цены по интервалам. Напр., в диапазоне от 100 до 200 (пик гистограммы) цена индекса находилась 13% времени, а в интервале от 0 до 300: 12% + 13% + 12% = 37%. Фактически гистограмма цены имеет случайный характер. Никаких сколько-либо выраженных закономерностей на ней не наблюдается. Средняя цена 669.19 не является самой частой, типичной. Это просто формальное число. Подобную картину можно наблюдать, если построить гистограмму любого другого фондового индекса или акции.
Связано это с тем, что динамика цен многих инструментов неплохо описывается моделью так называемого «случайного блуждания со сносом». Возьмите тетрадку в клеточку. Киньте монетку. Если выпадет «орел», нарисуйте «свечку» вверх на две клеточки, если «решка» – на две клеточки вниз. Независимо от выпадения монеты всегда приплюсовывайте и к бычьей и к медвежьей свечке одну клеточку вверх – это и есть «снос» или, другими словами, тренд. Если не полениться и провести множество бросаний монеты, полученный график будет довольно похож на график цены какой-нибудь акции. При помощи компьютера можно добиться еще большего реализма, генерируя свечи вверх и вниз случайного размера. Гистограмма цены не содержит какого-либо выраженного паттерна по причине ее случайного блуждания. Нет никаких экономических механизмов, которые бы возвращали цену акции к ее среднему значению. По этой причине она блуждает сама по себе обычно с некоторым положительным трендом. Средняя цена, таким образом, не может быть инвариантом. Продолжим поиск…
Добавим смысла
Что если вместо самой цены рассматривать ее дневные приращения? Например, вместо самого значения индекса брать его дневные изменения в пунктах. Для акции это будет дневное изменение цены в рублях или долларах – логика при этом такая же.
Линейная доходность
Тем не менее, среднее изменение цены нельзя признать инвариантом. По мере роста цены акции или уровня индекса диапазон ее колебаний также будет расти. Допустим, некоторая акция торгуется сейчас в районе 10 рублей. Тогда увеличение ее цены на 1 рубль будет составлять 10%. Предположим, через несколько лет акция выросла до 100 рублей. Рост на 1 рубль для нее будет уже только 1%. Один рубль для 10-рублевой и 100-рублевой акции – совсем разные вещи, поэтому инвесторы ориентируются не на денежную, а на процентную доходность, т.е. не на абсолютные, а на относительные величины. Процентная доходность не зависит от текущего уровня цен. Она более устойчива и, следовательно, более достойна звания инварианта. Рассчитать процентную доходность очень просто. Для этого нужно знать лишь цену открытия (O) и цену закрытия (C):
Процентная доходность на первый взгляд кажется наиболее естественно характеристикой фининструмента. Она не зависит от уровня цены. Кроме того, на ней очень интуитивно отражается влияние кредитного плеча – она просто умножается на коэффициент рычага: 1% доходность при плече 1:2 превращается в 2% и т.п. По этой причине ее еще называют линейной доходностью, поскольку рычаг воздействует на нее линейным образом.
Логдоходность
Логарифмическая доходность (или просто логдоходность) лишена этого недостатка линейной доходности. Она рассчитывается по формуле:
и принимает значения от «минус» до «плюс бесконечности». Символ ln() обознает функцию натурального логарифма. Что это за функция? В математике кроме знаменитого числа π есть еще и число e. Оно приблизительно равно 2.7183. Натуральный логарифм – это степень, в которую нужно возвести число e, чтобы получить число под знаком логарифма. Например, если число e, 2.7183, возвести в квадрат (степень 2), получится: 2.71832 2 = 7.3891. Отсюда следует, что ln(7.3891) = 2. Собственно, чтобы пользоваться логарифмами, не обязательно знать все эти тонкости. Функция логарифма является стандартной, ее легко можно вычислить на компьютере, пользуясь калькулятором Windows или Excel и т.п.
За неделю цена выросла на 2.95%. Умножение, однако, не очень удобная и интуитивная операция. Если перейти к логдоходностям, можно заменить ее сложением:
Дорога домой
Итак, в поисках инвариантов мы проделали довольно долгий путь от цены, через ее приращения и линейные доходности к такой довольно абстрактной вещи как логдоходность. Гистограмма логдоходности как и гистограмма приращений имеет выраженный пик, поэтому средняя логдоходность является и наиболее ожидаемой, наиболее вероятной. Она, как и линейная доходность, не зависит от текущего уровня цен. И, наконец, она симметрична относительно нуля, поскольку может принимать любые отрицательные и положительные значения. Все это позволяют охарактеризовать ее как натуральный рыночный инвариант. Превратить же цены в логдоходности достаточно просто при помощи MATLAB, Excel или других табличных редакторов.
Сейчас существует большое количество программ для прогнозирования адресованных трейдерам, например, нейросетевых. Они просты в управлении и не требуют специальных знаний. Типичная ошибка новичка при использовании такого софта в том, что он пытается «предсказать» непосредственно будущую цену по прошлым ценам. Однако, как мы убедились, изучив гистограмму, прогнозирование самой цены «в лоб» лишено какого-либо вероятностного смысла. Лучше всего прогнозировать будущую логдоходность по прошлым логдоходностям того же самого инструмента или других инструментов, если предполагается межрыночное взаимодействие. Это максимально упростит работу программе, поскольку ей не надо будет тратить силы на поиск очевидных закономерностей: что приращения цены зависят от ее уровня, и что они скошены в положительную сторону.
Хорошо, допустим, все это сделано, и программа выдает прогноз: завтрашняя дневная логдоходность составит 0.03. Как это понимать и использовать на практике? Необходимо конвертировать прогноз логдоходности в прогноз цены при помощи обратного преобразования. Делается это очень просто. Предположим, что текущая цена акции 100 рублей. Тогда прогноз завтрашней цены можно получить по формуле:
100 р.*exp(0.03) = 100 р.*1.0305 = 103.05 р.
Функция exp() – это уже знакомое нам число e в степени икс. Это просто альтернативный вариант записи, часто используемый в компьютерных приложениях. Экспонента является обратной по отношению к логарифму функцией, поэтому, подставляя в нее логдоходность, сразу же получаем коэффициент роста, на него и надо умножить текущую цену, чтобы получить прогноз будущей.
Резюме
Таким образом, мы убедились, что логдоходности – очень удобный аналитический инструмент. Их можно складывать, они не зависят от уровня цен и симметричны относительно нуля. На практике, если нужно получить прогноз или исследовать какие-либо вероятности движения цен следует использовать именно логдоходности.
Логдоходности легко конвертируются из одного тайм-фрейма в другой. Например, если вы хотите перевести дневную логдоходность в годовую, нужно просто умножить ее на количество торговых дней (около 250). Если затем взять экспоненту от этого числа, будет получен годовой темп роста капитала для торговой стратегии. Его удобно сравнивать с текущими банковскими ставками, доходностью фондовых индексов и других эталонных инструментов.
————————————————————————
Какую шкалу графика выбрать
При подготовке инструкции по работе с графиками на сайте Stockcharts.com я не уточнила такой важной момент, как выбор шкалы. Уточняю. Если вы посмотрите на график движения цены, то увидите на нем две оси. По горизонтальной оси X отложено время, по вертикальной оси Y – цена.
Инвестиции в акции США, IPO и Pre-IPO
Для оси X используется арифметическая (линейная) шкала. Для оси Y может применяться как арифметическая, так и логарифмическая шкала. В чем их отличие?
Арифметическая шкала показывает простое изменение цены в количестве пунктов или долларов. Логарифмическая шкала показывает не абсолютное изменение цены, а относительное, то есть не в количестве пунктов или долларов, а в процентном соотношении.
На арифметической шкале все единичные отрезки имеют одинаковую длину. Интервалы логарифмической шкалы не равны, так как с ростом цены процентные изменения уменьшаются и, как следствие, отрезки становятся уже, а деления чаще.
Принцип построения арифметической шкалы
Арифметическая шкала строится от нуля и с помощью сложения и вычитания. При перемещении вправо от нуля значения складываются, а при перемещении влево от нуля – вычитаются. Значение показателя по мере продвижения оси изменяется на равную величину. В результате отрезок шкалы 10-20 будет равен отрезку 100-110, несмотря на то, что в первом варианте изменение составит 100% (2 раза), а во втором – лишь 10%.
Принцип построения логарифмической шкалы
В логарифмической шкале равным отрезкам соответствует одинаковое процентное изменение показателя. Например, отрезок шкалы 10-20 будет равен отрезкам 20-40 и 40-80, т.е. изменение показателя во всех случаях составит 2 раза. Данная шкала строится от единицы с помощью умножения и деления. И для того чтобы переместиться на такое же расстояние как в арифметической шкале, например, на 10, необходимо 1 умножить на 10. В свою очередь, для перемещения на 10 влево, нужно 1 разделить на 10.
Отображение графиков с разной шкалой
При работе с графиками на коротких интервалах времени разница между арифметическим и логарифмическим способами шкалирования едва заметна. Однако при больших ценовых колебаниях и длительных периодах различия существенны. Эта хорошо видно на рисунке ниже. На нем я наложила графики индекса NYSE Composite ($NYA) за более чем 20-летний период. Менее четкая линия – это линия графика, построенного по логарифмической шкале.

Живая версия графиков доступна здесь и здесь.
Обратите внимание, что диапазон колебаний на графике с арифметической шкалой выше, чем с логарифмической. Кроме этого, на графике с арифметической шкалой есть ощущение более существенного движения и изменения. Поэтому такой способ построения любят СМИ: он позволяет преувеличить значения показателей и раздуть новость. Этого не происходит, когда данные отображаются на логарифмической шкале. И именно ее я рекомендую использовать при работе с графиками, охватывающими данные за длительный период.
Логарифмическая шкала цен для трендовых линий
Трендовые линии имеют интересное свойство: проявлять себя на графиках с логарифмической ценовой шкалой (а не арифметической). Если в абсолютном отношении на графике можно наблюдать ускорение роста цены (или замедление падения), то на этом же графике но с относительной (т.е. логарифмической) шкалой цен, вероятно, проявится отчетливая линия тренда. Следовательно, стоит просматривать график ценной бумаги в обоих режимах ценовой шкалы (логарифмическом и арифметическом) для поиска трендовых линий.
Напомним, что логарифмическая шкала цен показывает относительный прирост; на такой шкале, разница между отметками 10 и 20 равна разнице между отметками 20 и 40 (40 и 80, 80 и 160 и т.д. ), т.к. у обеих пар разница измеряется в относительном отношении; то есть разница во всех парах одинаковая, и составляет 100%. На шкале все эти разницы имеют одинаковое расстояние. А на арифметической шкале, разница между этими парами чисел была бы существенной, т.к. арифметическая шкала измеряет прирост абсолютный.
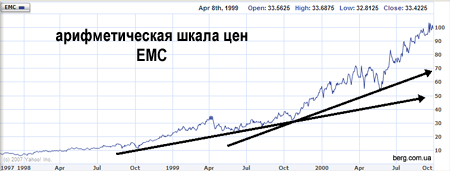
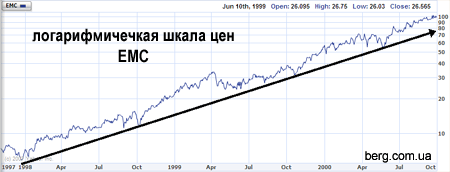
Вот пример для сравнения. На двух диаграммах изображен график цены на акции EMC Corporation (EMC). Период отображения — одинаковый: рост с 1998 по 2001 год.
Обратите внимание: за 2 с половиной года цена акций увеличилась в 10 раз. Для того, чтоб провести восходящие трендовые линии на арифметическом графике, потребовалось бы 2 (или более) трендовых линий. Но на графике с логарифмической шкалой цен, идеально вписывается одна восходящая линия тренда, которая описывает экспоненциальный прирост цены акции EMC.