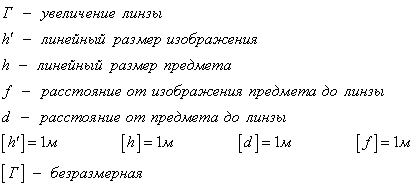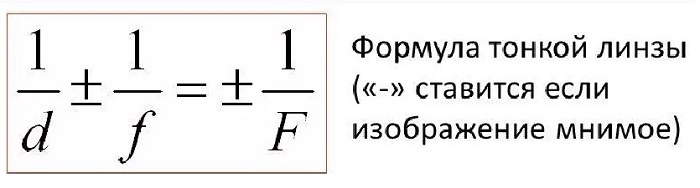что такое линзы формула линзы

IV. Оптика

Тестирование онлайн

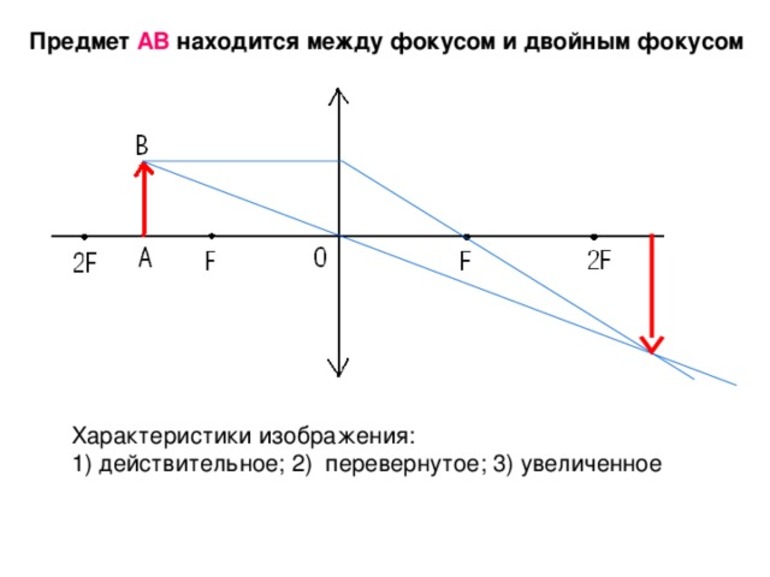
Характеристики изображения

1) Изображение может быть мнимое или действительное. Если изображение образовано самими лучами (т.е. в данную точку поступает световая энергия), то оно действительное, если же не самими лучами, а их продолжениями, то говорят, что изображение мнимое (световая энергия не поступает в данную точку).

2) Если верх и низ изображения ориентированы аналогично самому предмету, то изображение называется прямым. Если же изображение перевернуто, то его называют обратным (перевернутым).

3) Изображение характеризуется приобретаемыми размерами: увеличенное, уменьшенное, равное.

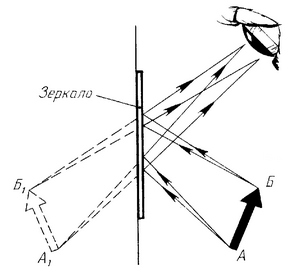
Изображение в плоском зеркале

Изображение в плоском зеркале является мнимым, прямым, равным по размерам предмету, находится на таком же расстоянии за зеркалом, на каком предмет расположен перед зеркалом.

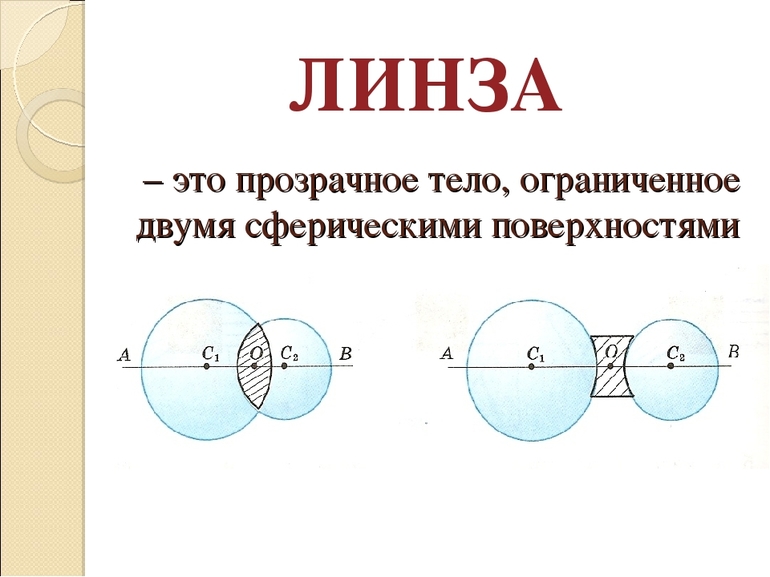
Линзы

Линза представляет собой прозрачное тело, ограниченное с двух сторон криволинейными поверхностями.

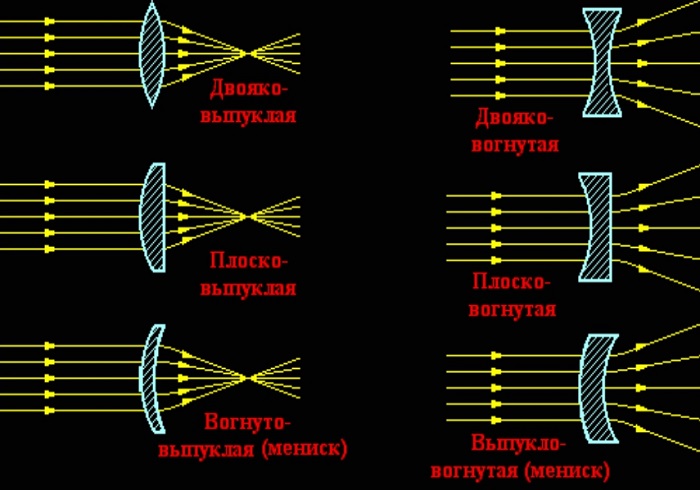
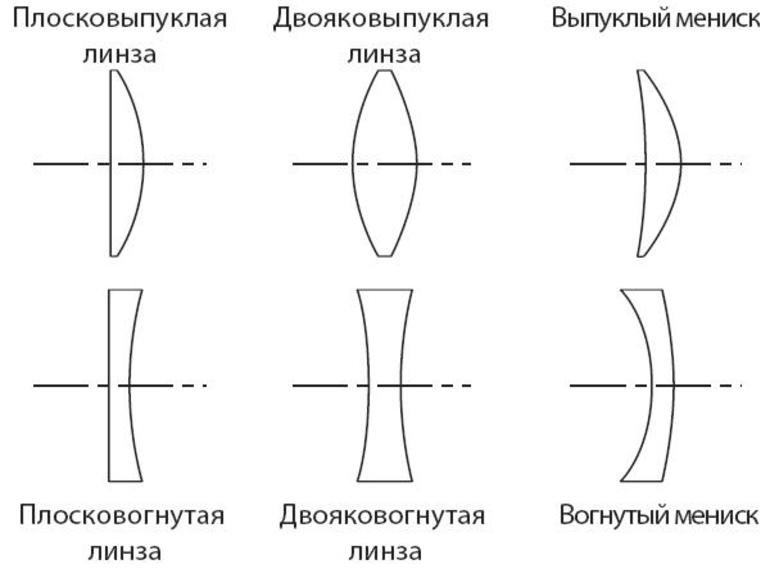
Различают шесть типов линз.

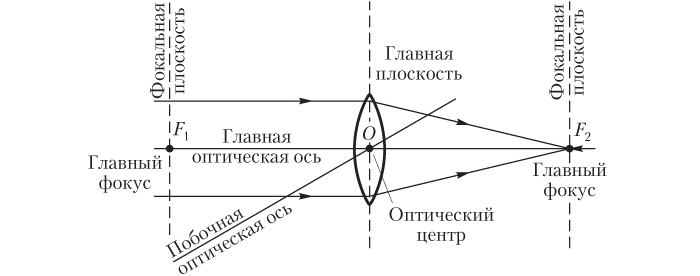
O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре);

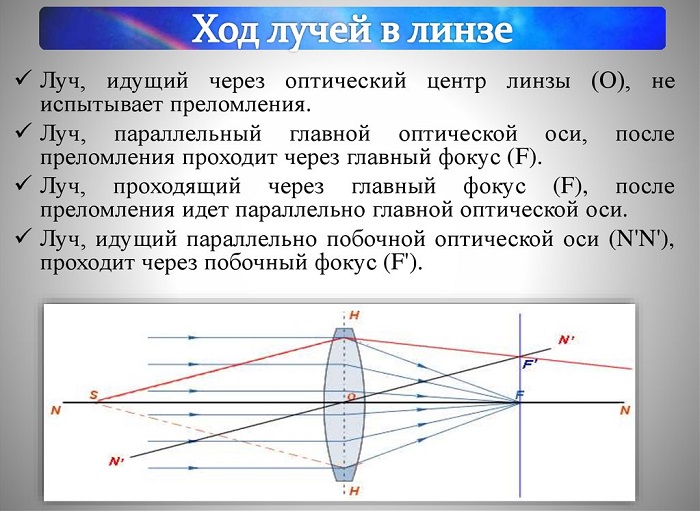
Луч, идущий через оптический центр линзы (О), не испытывает преломления.

Луч, параллельный главной оптической оси, после преломления проходит через главный фокус (F).

Луч, проходящий через главный фокус (F), после преломления идет параллельно главной оптической оси.

Луч, идущий параллельно побочной оптической оси (N’N’), проходит через побочный фокус (F’).

Величина, обратная фокусному расстоянию линзы, называется оптической силой.

Современные оптические устройства используют системы линз для улучшения качества изображений. Оптическая сила системы линз, сложенных вместе, равна сумме их оптических сил.

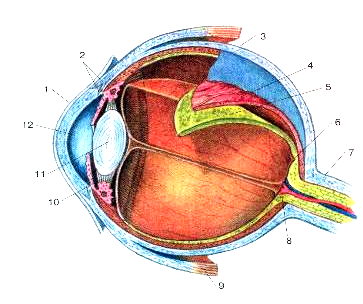
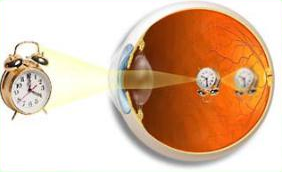
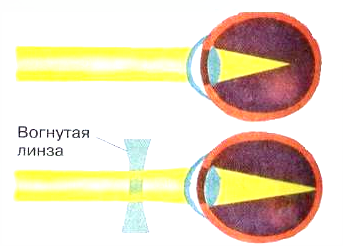
Хрусталик является линзоподобным телом и осуществляет настройку нашего зрения на различные расстояния. В оптической системе глаза фокусировка изображения на сетчатку называется аккомодацией. У человека аккомодация происходит за счет увеличения выпуклости хрусталика, осуществляемого с помощью мышц. При этом изменяется оптическая сила глаза.

Изображение предмета, попадающее на сетчатку глаза, является действительным, уменьшенным, перевернутым.

Расстояние наилучшего зрения должно быть около 25 см, а предел зрения (дальняя точка) находится на бесконечности.

Источник

Линза. Виды линз. Фокусное расстояние.

теория по физике 🧲 оптика

Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.

Линза — прозрачное тело, ограниченное сферическими поверхностями.

Какими бывают линзы?

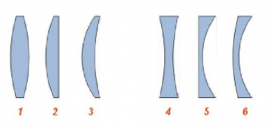
По форме различают следующие виды линз:

Выпуклые линзы тоже имеют разновидности:

Разновидности вогнутых линз:

Тонкая линза

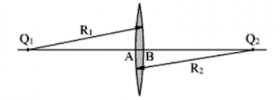
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R₁ и R₂. Такие линзы называют тонкими.

Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.

Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O₁O₂).

Оптический центр линзы — точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.

Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.

Изображение в линзе

Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.

Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.

Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.

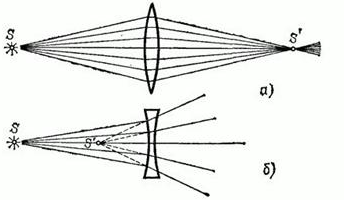
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.

Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.

Собирающая линза

Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.

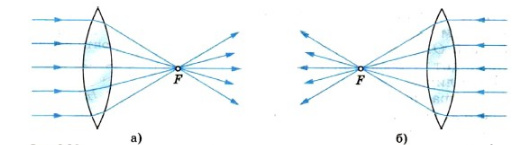
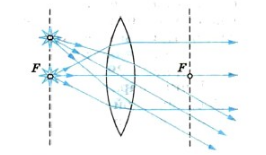
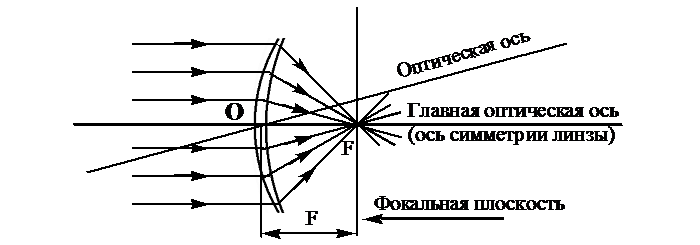
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.

Главный фокус линзы обозначают буквой F.

Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).

В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.

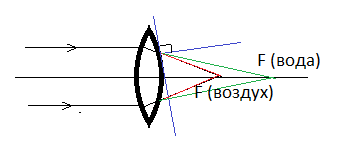
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?

Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.

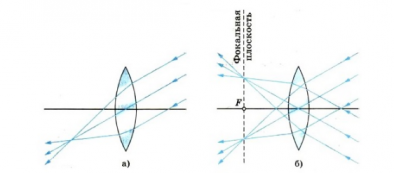
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.

Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.

Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.

Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.

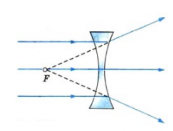
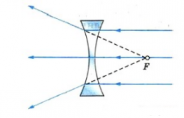
Рассеивающая линза

Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.

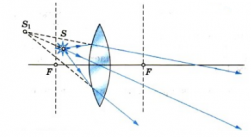
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.

Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.

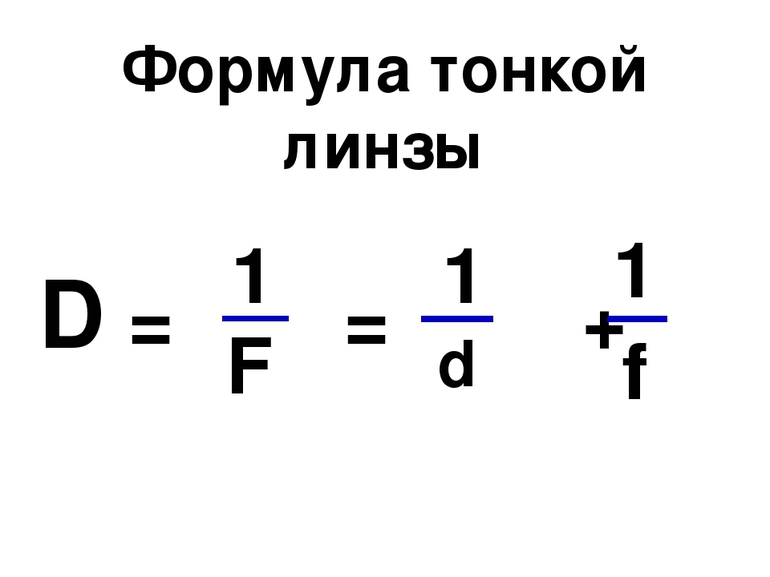
Оптическая сила линзы

Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.

Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.

Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:

На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу. Какова приблизительно оптическая сила этой линзы?

Источник

Формула тонкой линзы

теория по физике 🧲 оптика

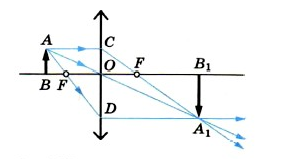
Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.

Вывод формулы

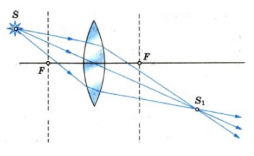
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:

Видно, что треугольники АОВ и А₁В₁О подобные (по двум углам). Следовательно:

По двум углам также являются подобными треугольники COF и FA₁B₁. Отсюда делаем вывод, что:

Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:

Отсюда следует, что:

B O является расстоянием от предмета до линзы. Обозначим его за d. O B 1 является расстоянием от линзы до изображения. Обозначим его за f. O F является фокусным расстоянием линзы. Обозначим его за F. F B 1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:

Избавимся от знаменателей и получим:

Или можно записать так:

Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:

Формула тонкой линзы

Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:

Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.

Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.

Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.

Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.

Применим формулу тонкой линзы:

Умножим выражение на 150d:

Увеличение линзы

Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.

Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А₁В₁ равна Н, то:

Мы уже выяснили, что треугольники АОВ и ОА₁В₁ подобны. Поэтому:

Где H — высота изображения предмета, h — высота самого предмета.

Отсюда вытекает, что увеличение линзы равно:

Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?

Сначала применим формулы тонкой линзы:

Она необходима, чтобы выразить фокусное расстояние линзы:

Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:

Отсюда это расстояние равно:

Подставим полученное выражение в формулу фокусного расстояния линзы:

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Источник

Если бы не существовало такой детали, как линза, физика, как и другие науки, не смогла бы преобразовать наш мир.

Люди не смогли бы наблюдать бесконечность космоса сквозь телескоп и бесконечность жизни через микроскоп, скрупулёзно занося свои наблюдения в различные таблицы. Пытаясь найти свое место во Вселенной и понять свое происхождение, человек создал Большую Науку.

Что такое линза

Увеличительные стекла были известны еще с древних времен. По форме они очень напоминали чечевицу (lens на латыни), что и дало им современное название. Применялись они для увеличения изображений слабовидящими.

Линза в оптике – это кусок стекла или любого другого прозрачного материала с гладкой полированной поверхностью сферической формы.

Благодаря этим особенностям она способна изменять направление света, проходящего сквозь него, и потому применяется во множестве приборов.

Виды линз

В зависимости от того, как ведут себя проходящие через них лучи света, они бывают собирающие и рассеивающие.

Первые имеют выпуклую форму с обеих сторон и называются двояковыпуклыми. Кроме того, бывают плоско-выпуклые и выпукло-вогнутые.

Рассеивающие имеют вогнутую форму и называются двояковогнутыми. Конечно, есть и другие формы: вогнуто-плоские и вогнуто-выпуклые.

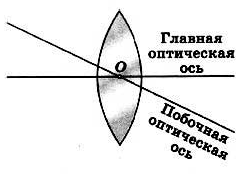
Главная оптическая ось линзы

Свет, проходящий через сферическую поверхность, ведет себя необычно. У самого края он преломляется сильнее, чем у центра. Связано это с тем, что у края кривизна сильнее.

Таким образом, чем ближе к центру будет проходить луч, тем меньше он будет отклоняться в сторону. И в геометрическом центре линзы, который еще называют оптическим центром, свет вообще не будет преломляться и пройдет как через обычное оконное стекло.

Если у симметричных этот центр находится внутри, то у остальных разновидностей он может находиться за ее пределами.

Пропущенная через эту точку прямая, которая повторит ход пройденного и оставшегося непреломленным луча, будет называться главной оптической осью.

Фокус линзы и фокусное расстояние

Чтобы понять, что такое фокус линзы, лучше всего представить себе ее собирающий класс.

Пучки света, пройдя через нее, должны будут пересечься в какой-то точке, которая будет находиться на главной оптической оси. Эта точка и называется фокусом.

Она есть и у рассеивающих линз, но, чтобы найти ее, нужно продолжить расходящиеся лучи в обратную сторону. Будет казаться, что они все вышли из одной точки по эту сторону от нее. Это и будет фокус, но в данном случае он мнимый, а не действительный.

Расстояние от оптического центра до фокуса именуется фокусным расстоянием. Оно может быть положительным и отрицательным.

Со знаком «+» оно для собирающих, а для рассеивающих – со знаком «-».

Ход лучей в линзе

Для того чтобы легче просчитывать построение изображения в линзе, принято брать схематическое ее обозначение, сильно идеализированное. Ее называют тонкой. Считается, что ее толщина намного меньше, чем радиусы ее кривизны. Это позволяет упростить многие задачи по оптике.

Как упоминалось выше, свет, проходящий через оптический центр, никак не преломляется. Причем это свойство соблюдается, под каким бы углом он ни падал. У таких побочных оптических осей тоже существуют свои фокусы, которые тоже являются побочными.

Теперь, когда основные понятия обозначены, можно приступать к рассмотрению хода лучей:

Пересекая собирающую линзу, лучи соберутся за ней в фокусе.

То же справедливо и для обратного случая: если в фокусе разместить источник света, то лучи от него будут вначале расходиться, а после нее пойдут параллельно друг другу.

В случае вогнутых стекол они будут расходиться в разные стороны, а по эту сторону в мнимом фокусе будет светящаяся точка.

Если лучи падают наклонно, то они соберутся вместе в побочном фокусе. Найти его легко: через оптический центр нужно пропустить прямую под нужным углом до фокальной плоскости.

Если лучи падают под определенным углом в рассеивающей линзе, то побочный фокус находится ровно там же, но фокальная плоскость будет проходить через мнимый фокус. Соответственно, прямая от оптического центра продолжается до него, где и будет точка, откуда как будто бы они расходятся.

Формула линзы

Существует закономерность между фокусным расстоянием, расстояниями от линзы до предмета и до его изображения. Все это хорошо описывает следующая формула:

Знаки «±» здесь не случайны. Как уже говорилось, все зависит от вида линзы: для собирающей это «+», а для рассеивающей будет «-».

Латинская буква d означает расстояние до предмета, f – расстояние до его изображения, F — фокусное расстояние.

Источник

Общие сведения

Согласно физическому определению, под линзой понимают оптическую систему, которая состоит из прозрачного для электромагнитных волн вещества, и которая ограничена хотя бы одной кривой поверхностью (вторая может быть плоской). Прозрачное вещество должно обладать способностью преломлять свет, что возможно, если оно имеет отличный от окружающей среды коэффициент преломления. Оптический объект будет только тогда обладать всеми своими свойствами, если коэффициент преломления вещества, из которого он изготовлен, будет больше этого показателя для окружающей среды.

Слово «линза» произошло от латинского lentis, которое означает «чечевица». Такое название связано с похожестью формы оптического объекта и плода растения.

Линзы используются человеком издревле для разных хозяйственных нужд. Так, в своей работе «Облака» (423 год до нашей эры) греческий философ Аристофан упоминает об их применении в качестве предмета для размягчения воска с помощью фокусировки солнечных лучей. Начиная с XV века, в Европе возникает индустрия производства оптики. С этого времени развивается теоретическая база для ее использования.

Виды и типы

Существует огромное многообразие оптических линз. Однако все они могут быть сгруппированы по определенным физическим критериям:

При изучении физических свойств оптических стекол пользуются их упрощенным изображением. Выпуклые линзы показывают в виде отрезка со стрелками на его концах, обращенными наружу. Для рассеивающих стекол эти стрелки обращены внутрь.

Существует еще один критерий, который определяет характер прохождения лучей через рассматриваемые типы объектов. Речь идет о сравнении показателей преломления вещества и окружающей среды. Предполагают, что это значение для оптического объекта n’ больше, чем для среды n (n’>n). Для воздуха n=1, поэтому n’ должен быть больше 1.

Основная формула

Существует выражение, которое позволяет определить любую характеристику оптического стекла. Оно называется фундаментальная формула линзы. Иногда его также называют уравнением изготовителя оптических стекол. Это выражение устанавливает четкую связь между расстоянием от объекта s и его изображения s’ и показателями преломления вещества линзы и окружающей среды, а также радиусами кривизны R1, R2. Сформулировать его можно так:

n/s’ — n/s = (n’-n)*(1/R1 — 1/R2).

Фундаментальное уравнение можно найти самостоятельно, если рассмотреть преломление одного луча через каждую из искривленных поверхностей. Это выражение справедливо для всех типов рассматриваемых объектов.

Понятие о фокусе

Когда изучают тонкие оптические стекла, то особое внимание уделяют фокусному расстоянию предмета f и его изображения f’. Определения этих величин следующие:

Учитывая определения фокусных расстояний предмета и его изображения, а также привлекая фундаментальное уравнение, можно записать следующую взаимосвязь между f и f’:

Полученные выражения можно использовать для выведения гауссового вида формулы тонкой линзы. Она имеет следующую форму:

Это выражение справедливо для любых сред, а не только для воздуха. Оно также называется формулой фокусного расстояния линзы.

Гауссова форма

Ее использование позволяет сделать несколько важных выводов. Для их получения удобно переписать ее в следующем виде:

Источник