что такое линейный угол двугранного угла

Двугранный угол (ЕГЭ 2022)

Дай нам 10 минут ты разберешься в одной из самых важных тем стереометрии.

И получишь за неё баллы на ЕГЭ!

Двугранный угол — коротко о главном

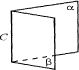
Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.

Угол между плоскостями – наименьший из двугранных углов, образованных при пересечении плоскостей.

Двугранный угол может быть и острым и тупым, а угол между плоскостями только острым! НЕ ПУТАЙ!

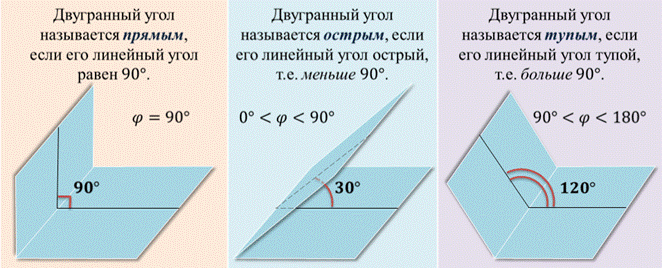
Прямой двугранный угол – двугранный угол, который равен \( \displaystyle 90<>^\circ \), то есть тот, у которого линейный угол равен \( \displaystyle 90<>^\circ \).

Два способа найти угол между плоскостями:

Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.

Двугранный угол — определения

Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.

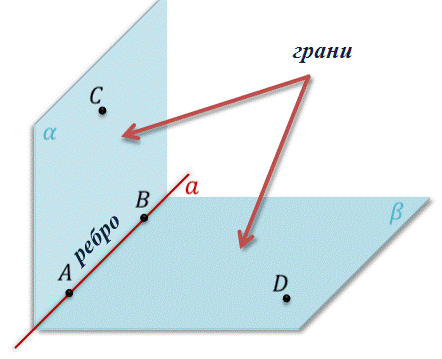
При этом прямая \( \displaystyle AB\) – это ребро двугранного угла, а полуплоскости \( \displaystyle \alpha \) и \( \displaystyle \beta \) – стороны или грани двугранного угла.

Двугранный угол получает обозначение по своему ребру: «двугранный угол \( \displaystyle AB\)».

С понятием двугранного угла тесно связано понятие угол между плоскостями.

Угол между плоскостями – наименьший из двугранных углов, образованных при пересечении плоскостей.

Итак, внимание! Различие между двугранным углом и углом между плоскостями в том, что:

Двугранный угол может быть и острым, и тупым, а угол между плоскостями только острым! НЕ ПУТАЙ!

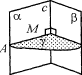
Линейный угол двугранного угла

Как измерить двугранный угол?

Нужно поступить так: из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру.

В плоскости \( \displaystyle \alpha \) провели перпендикуляр \( \displaystyle MD\) к ребру \( \displaystyle AB\). Что получилось? Обычный, плоский угол \( \displaystyle \varphi \).

Вот этот угол и называется: линейный угол двугранного угла \( \displaystyle AB\).

Зачем этот линейный угол? Запомни, это очень ВАЖНО:

Двугранный угол измеряется величиной своего линейного угла.

То есть математически договорились, что если угол φ будет равен, к примеру \( \displaystyle 20<>^\circ \), то это будет автоматически означать, что угол \( \displaystyle AB\) равен \( \displaystyle 20<>^\circ \).

Вот и ключ к поиску величины двугранного угла и угла между плоскостями:

Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.

Ещё раз немного о названиях.

Прямой двугранный угол – двугранный угол, который равен \( \displaystyle 90<>^\circ \), то есть тот, у которого линейный угол равен \( \displaystyle 90<>^\circ \).

Как найти угол между плоскостями?

Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.

Геометрический способ

При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.

Алгебраический способ

Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.

Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!

Какой же способ лучше? Зависит от задачи.

А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.

Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать \( \displaystyle <_<1>>,<_<1>>,<_<1>>,<_<2>>,<_<2>>,<_<2>>\), а потом ещё и \( \displaystyle \cos \gamma \).

Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.

Решение геометрическим способом

В правильной треугольной пирамиде боковое ребро в три раза больше ребра основания. Найти двугранный угол при основании пирамиды.

Источник

Двугранный угол. Линейный угол двугранного угла

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей прямой, которая их ограничивает.

Полуплоскости α и β — грани двугранного угла.
C — ребро двугранного угла (рис.33)

Линейным углом двугранного угланазывается угол между лучами, по которым плоскость, перпендикулярная ребру двугранного угла, пересекает его грани.

Плоскость линейного угла перпендикулярна каждой грани двугранного угла (рис.34)

Способы построения линейного угла:

На ребре выбирается точка, через нее в гранях проводятся лучи, перпендикулярные ребру. Угол, образованный этими лучами, и будет искомым линейным углом (рис.35)

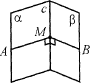
∠AMB — линейный

Источник

Скоро вебинар
«ПРЯМАЯ НА ПЛОСКОСТИ»
(Аналитическая геометрия). Жми подробнее.

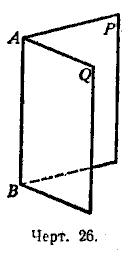
Если в плоскости γ провести две пересекающиеся прямые АК и BN в точке М, то плоскость разделится ими на 4 области, которые образуют 4 «плоских » угла.

Аналогично две пересекающиеся плоскости γ и β по прямой АВ, делят пространство на 4 области и образуют 4 двугранных угла.

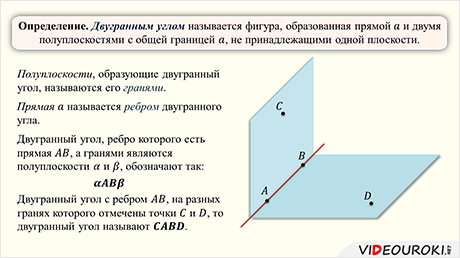
Определение. Двугранный угол – это фигура, образованная прямой АВ и двумя полуплоскостями с общей границей АВ, не принадлежащей одной плоскости.

Полуплоскости, образующие двугранный угол, называются гранями двугранного угла.

Общая для граней прямая АВ (граница полуплоскостей) называется ребром двугранного угла.

Обозначение: KABL, где K и L-это точки, лежащие в разных гранях, а АВ – ребро двугранного угла.

Измерение двугранных углов сводится к измерению линейных углов.
Определение. Линейным углом двугранного угла называется плоский угол, образованный двумя лучами, которые лежат в гранях этого двугранного угла и перпендикулярны его ребру.

Все линейные углы данного двугранного угла равны между собой.

За величину двугранного угла принимают величину его линейного угла.
Выражение двугранный угол равен ᵠ означает, что величина соответствующего линейного угла равна ᵠ.

Двугранный угол называется прямым (острым, тупым), если он равен 90°(меньше 90°, больше 90°)

Источник

Двугранные углы

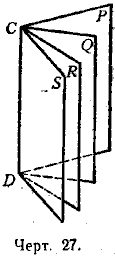
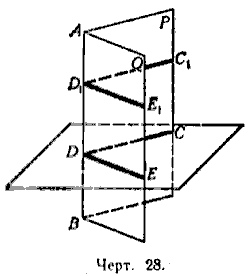
Если из произвольной точки D ребра AB (черт. 28) проведём на каждой грани по перпендикуляру к ребру, то образованный ими угол CDE называется линейным углом двугранного угла.

Величина линейного угла не зависит от положения его вершины на ребре. Так, линейные углы CDE и C₁D₁E₁ равны, потому что их стороны соответственно параллельны и одинаково направлены.

Плоскость линейного угла перпендикулярна к ребру, так как она содержит две прямые, перпендикулярные к нему. Поэтому для получения линейного угла достаточно грани данного двугранного угла пересечь плоскостью, перпендикулярной к ребру, и рассмотреть получившийся в этой плоскости угол.

Равенство и неравенство двугранных углов

Два двугранных угла считаются равными, если они при вложении могут совместиться; в противном случае тот из двугранных углов считается меньшим, который составит часть другого угла.

Подобно углам в планиметрии, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

1) Равным двугранным углам соответствуют равные линейные углы.

2) Большему двугранному углу соответствует больший линейный угол.

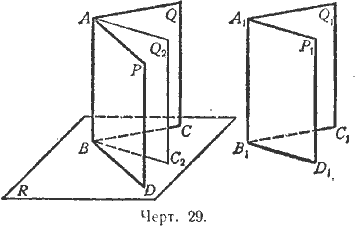
Тогда если эти двугранные углы равны, то грань Q₁ совпадёт с гранью Q; если же угол А₁В₁ меньше угла AB, то грань Q₁ займёт некоторое положение внутри двугранного угла, например Q₂.

Заметив это, возьмём на общем ребре какую-нибудь точку В и проведём через неё плоскость R, перпендикулярную к ребру. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы. Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол CBD; если же двугранные углы не совпадут, если, например, грань Q₁ займёт положение Q₂, то у большего двугранного угла окажется больший линейный угол (именно: ∠CBD > ∠C₂BD).

1) Равным линейным углам соответствуют равные двугранные углы.

2) Большему линейному углу соответствует больший двугранный угол.

Эти теоремы легко доказываются от противного.

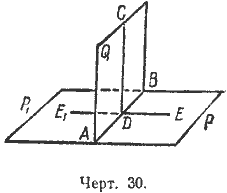
1) Прямому двугранному углу соответствует прямой линейный угол, и обратно.

Пусть (черт. 30) двугранный угол PABQ прямой. Это значит, что он равен смежному углу QABP₁. Но в таком случае линейные углы CDE и CDE₁ также равны; а так как они смежные, то каждый из них должен быть прямой. Обратно, если равны смежные линейные углы CDE и CDE₁, то равны и смежные двугранные углы, т.е. каждый из ни должен быть прямой.

2) Bcе прямые двугранные углы равны, потому что у них равны линейные углы.

Подобным же образом легко доказать, что:

3) Вертикальные двугранные углы равны.

4) Двугранные углы с соответственно параллельными и одинаково (или противоположно) направленными гранями равны.

5) Если за единицу двугранных углов возьмём такой двугранный угол, который соответствует единице линейных углов, то можно сказать, чтo двугранный угол измеряется его линейным углом.

Источник

Двугранный угол

Урок 22. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Двугранный угол»

· введем понятие двугранного угла;

· узнаем о том, как определить линейный угол рассматриваемой геометрической фигуры.

Для начала давайте вспомним, что понимали под углом в планиметрии. Итак, углом на плоскости мы называлигеометрическую фигуру, образованную двумя лучами, исходящими из одной точки.

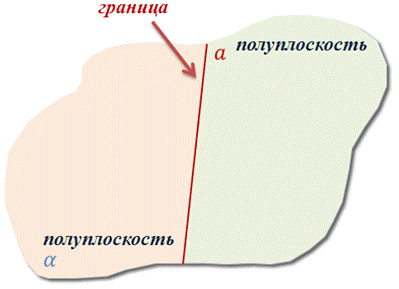
В стереометрии наряду с такими углами рассматривается еще один вид углов, которые называют двугранными углами. Но прежде чем мы введем понятие двугранного угла, давайте вспомним одну из аксиом планиметрии: «любая прямая, проведенная в данной плоскости, разделяет эту плоскость на две полуплоскости».

Пусть есть прямая а, которая лежит в некоторой плоскости. Тогда можно указать две части этой плоскости, каждая из которых вместе с прямой а называется полуплоскостью.

Прямая а называется границей для каждой из полуплоскостей. В отличие от планиметрии, в пространстве две полуплоскости с общей границей прямой а, могут не лежать в одной плоскости.

Давайте представим себе, что мы перегнули плоскость по прямой а так, что две полуплоскости с границей а оказались уже не лежащими в одной плоскости. Полученная фигура и есть двугранный угол.

Определение. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.

Полуплоскости, образующие двугранный угол, называются его гранями. У двугранного угла две грани, отсюда и название – двугранный угол.

Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.

Двугранный угол, ребро которого есть прямая AB, а гранями являются полуплоскости α и β, обозначают так 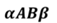. Обратите внимание, две средние буквы в обозначении – это ребро данного двугранного угла.

Или, если двугранный угол с ребром AB, на разных гранях которого отмечены точки C и D, то двугранный угол называют CABD.

В обыденной жизни мы часто встречаемся с предметами, имеющими форму двугранного угла. Представление о двугранном угле нам дают: полураскрытая книга, открытый ноутбук, двускатная крыша здания, стена комнаты совместно с полом и т.д.

Напомню, что углы на плоскости измеряются в градусах.

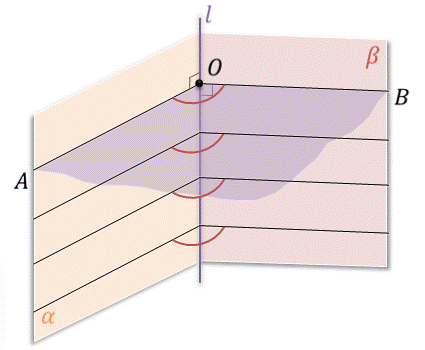
Для измерения двугранного угла вводится понятие линейного угла. Пусть точка О лежит на ребре l двугранного угла. В каждой грани из этой точки проведем лучи ОА и ОB перпендикулярно к ребру l. Угол АОB, сторонами которого служат лучи ОА и ОB, называется линейным углом данного двугранного угла.

Определение. Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.

На рисунке вы видите изображение линейного угла AOB двугранного угла с ребром l. Так как ОА перпендикулярно l и ОB перпендикулярно l, то плоскость, в которой лежат лучи ОА и ОB, перпендикулярна к прямой l. Таким образом, плоскость линейного угла перпендикулярна к ребру двугранного угла. Очевидно, двугранный угол имеет бесконечное множество линейных углов.

Верно следующее утверждение: все линейные углы двугранного угла равны между собой.

Докажем это утверждение.

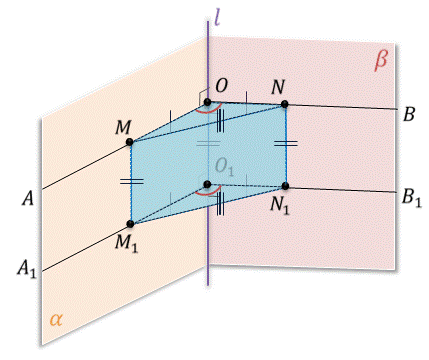
Рассмотрим два линейных угла А О Б и А один О один Б один двугранного угла,ребро которого эль. Лучи ОА и О один А один лежат в одной грани и перпендикулярны ребру эль. Следовательно, они параллельны. Аналогично и лучи ОБ и О один Б один лежат в одной грани и перпендикулярны ребру эль. Значит, они параллельны.

Отложим на лучах ОА и О₁A₁ равные отрезки OM и O₁M₁ соответственно, а на лучах ОB и O₁B₁ – равные отрезки ON и O₁N₁ соответственно.

Так как OM равно O₁M₁ и OM параллельно O₁M₁, то четырехугольник OMM₁O₁ – параллелограмм. Тогда ОО₁ равно MM₁ и OO₁ параллельно MM₁ по свойствам параллелограмма.

Так как ON равно O₁N₁ и ON параллельно O₁N₁, то четырехугольник ONN₁O₁ – параллелограмм. Тогда OO₁ равно NN₁ и OO₁ параллельно NN₁ по свойствам параллелограмма. Отсюда, OO₁ равно NN₁ и OO₁ параллельно NN₁.

Видим, что тогда MM₁ равно NN₁ и MM₁ один параллельно NN₁, т.е. четырехугольник NMM₁N₁ – параллелограмм. Следовательно, NM равно N₁M₁.

Рассмотрим треугольники OMN и O₁M₁N₁. Они равны по трем сторонам. Отсюда следует, что угол MON равен углу M₁O₁N₁. А значит, и угол АОB равен углу A₁O₁B₁. Что и требовалось доказать.

Это утверждение можно доказать и быстрее. Достаточно было при рассмотрении линейных углов AOB и A₁O₁B₁ заметить, что так как лучи ОА и O₁A₁ лежат в одной грани и перпендикулярны к прямой OO₁, то они параллельны, а, значит сонаправлены. Точно также лучи ОB и O₁B₁ лежат в одной грани и перпендикулярны к прямой OO₁, следовательно они параллельны, и, значит сонаправлены. Отсюда вытекает, что угол A₁O₁B₁ равен углу AOB (как углы с сонаправленными сторонами). Что и требовалось доказать.

Определение. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Это говорит о том, что, сколько градусов содержится в линейном угле, столько же градусов содержится в его двугранном угле.

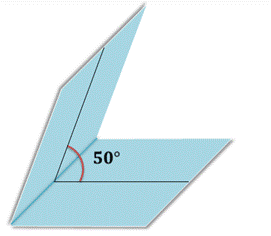
На рисунке вы видите изображение двугранного угла, градусная мера которого равна 50°. Обычно говорят коротко: «Двугранный угол равен 50°».

Различают следующие виды двугранных углов.

Двугранный угол называется прямым, если его линейный угол равен 90°.

Двугранный угол называется острым, если его линейный угол острый, т.е. 90° (расположен в промежутке от 90 до 180 градусов).

Если грани двугранного угла лежат в одной плоскости, то он называется развернутым.

В дальнейшем под двугранным углом будем понимать всегда тот, линейный угол φ которого удовлетворяет условию 0° Оцените видеоурок

Источник