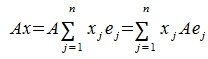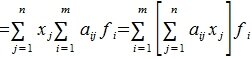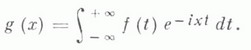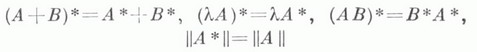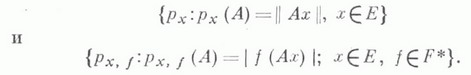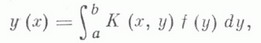что такое линейный оператор простым языком
Линейный оператор
Содержание
Линейный оператор [ править ]
| Определение: |
| Линейный оператор [math]\mathcal \colon X \to X[/math] называется автоморфизмом (или гомоморфизмом). |
| Определение: |
| [math]\mathcal |
Примеры [ править ]
Тождественный оператор [ править ]
[math]I \colon X \to X[/math] по формуле [math]Ix=x[/math]
Линейный оператор проектирования [ править ]
[math]\mathcal
_
[math]\mathcal
_
NB: [math]\mathcal
_
Оператор дифференцирования [ править ]
[math]\mathcal
Интегральный оператор [ править ]
[math](\mathcalf)(s) = \int\limits_a^b K(s,t) \cdot f(t) \cdot dt[/math]
[math]\mathcal \colon C(a,b) \to C(a,b)[/math]
Матрица линейного оператора [ править ]
Пусть п.п. [math]X \leftrightarrow \
Пусть п.п. [math]Y \leftrightarrow \
[math] A= \begin
| N.B.: |
| Обратите внимание, что [math]\mathcal[/math] означает оператор, а [math]A[/math] — матрицу этого оператора. |
Примеры [ править ]
Нулевой оператор [ править ]
[math] \mathcal
Оператор дифференцирования [ править ]
[math]\mathcal
[math] D= \begin
Теорема об эквивалентности задания линейного оператора [ править ]
[math] \Leftarrow x= \sum\limits_
Линейные операторы
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

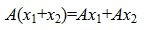 , , | (2) |
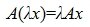 . . |
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
 | (3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
 | (4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
 | (6) |
Тогда равенство (5) примет следующий вид:
 | (7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 | (8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах 

2. Сложение линейных операторов
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
ЛИНЕЙНЫЙ ОПЕРАТОР
Вплоть до начала 20 в. систематически изучались лишь Л. о. между конечномерными пространствами над полями 
Помимо этого в теории Л. о. между пространствами с топологией важны задачи об аппроксимации различных классов Л. о. операторами сравнительно простого строения. Значительную роль играют задачи о нахождении общего вида Л. о. в конкретных, чаще всего функциональных, пространствах.
Понятие Л. о. является специальным случаем понятия морфизма модулей, к-рое получается при замене поля на произвольное кольцо. Морфизмы модулей во многом не похожи по свойствам на Л. о., однако именно результаты о последних явились одним из стимулов к их изучению.
Л. о. подобны тогда и только тогда, когда они могут быть записаны (каждый в «своем» базисе) одной и той же матрицей. Собственные значения Л. о. суть корни характеристич. многочлена его матрицы. Отсюда следует, что всякий Л. о. в конечномерном пространстве над алгебраически замкнутым полем (напр., 
Непрерывные линейные операторы в банаховых пространствах. Основы их теории заложены С. Банахом (см. [4]).
Примеры. 1) В l p (здесь и далее 

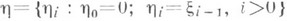
2) В 
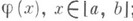
3) В 

4) Из 
Л. о. 

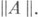
Заданная на 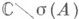
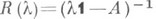
В теории Л. о. между банаховыми пространствами важна операция перехода от 

Эта операция обладает свойствами
(в предположении, что левые части равенств имеют смысл). Если Еи Fрефлексивны, то ( А*)*=А.
Некоторые важнейшие классы Л. о. в банаховых пространствах таковы.
1) 
Проблему классификации эндоморфизмов банаховых пространств, ввиду теоремы Жордана, дающей конечномерный образец ее решения, можно «в первом приближении» трактовать как проблему построения содержательного бесконечномерного аналога жордановой формы Л. о. Она, однако, далека от решения: не говоря о «достаточном» наборе инвариантных подпространств, до сих пор (1982) неизвестно, всякий ли оператор, действующий в гильбертовом пространстве Н, обладает хотя бы одним нетривиальным (отличным от (О) и Н).инвариантным подпространством. Если Л. о. А, действующий в произвольном банаховом пространстве, не пропорционален 1 и перестановочен с нек-рым компактным Л. о., то у всех Л. о., перестановочных с А, есть нетривиальное инвариантное подпространство (см. [9]).
Помимо топологии нормированного пространства, в В( Е, F).есть и другие топологии, задающие в нем структуру локально выпуклого пространства. Наиболее важны сильная и слабая операторные топологии, задаваемые системами полунорм соответственно
Непрерывные линейные операторы в гильбертовых пространствах (конечномерных и бесконечномерных). Их теория начала формироваться в работах Д. Гильберта [10] об интегральных уравнениях и бесконечных квадратичных формах.
Пример ы. 1) Все примеры Л. о. в 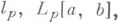

2) Интегральный оператор в L 2 [a, b], переводящий f(x)в
3) Оператор Фурье в 
Понятия и факты приведены ниже в той форме, какую они имеют для пространств над 
Для гильбертовых пространств характерны следующие классы Л. о.
Описанные классы Л. о. используются в целом ряде разделов математики и физики, в том числе в квантовой механике (где самосопряженные Л. о. интерпретируются как наблюдаемые),, в теории представлений и гармонич. анализе, в теории дифференциальных уравнений и в теории динамич. систем.
Всю информацию о Л. о., действующем в конечномерном гильбертовом пространстве, доставляет его матричная запись в ортонормированием базисе. В такой записи переходу к сопряженному Л. о. соответствует взятие матрицы, комплексно сопряженной к транспонированной; как следствие, для матрицы 


Теорема о приведении к диагональному виду оказалась «счастливее» теоремы Жордана в том отношении, что для нее найден содержательный бесконечномерный аналог: спектральная теорема для нормальных Л. о., открытая в 1912 (для самосопряженных Л. о.) Д. Гильбертом. Одна из ее формулировок: нормальный Л. о. однозначно представим в виде операторнозначного интеграла Стилтьеса 

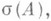

На основе теоремы Гильберта получена полная классификация нормальных линейных операторов (в пространстве любой размерности) с точностью до унитарной эквивалентности [11]; в частности, оказывается, что каждый нормальный Л. о. унитарно эквивалентен оператору умножения на ограниченную измеримую функцию в 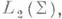
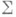
В случае нормального Аспектральная теорема позволяет придать смысл выражению функции f(А).для более широкого класса функций на спектре, чем голоморфные функции, напр. для непрерывной f Л- о. f(A).определяется как 
Лит.:[1] Реanо G., Calcolo geometrico secondo l’Ausdelmungslehre di H.. Grassmann, Torino, 1888; [2] Гельфанд И. М., Лекции по линейной алгебре, 4 изд., М., 1971; [3] Т о е р l i t 7. О., «Rend. Circolo mat. Palermo», 1909, v. 28, p. 88-96; [4] Банах С., Курс функционального аналiзу, Киiв, 1948; [5] Т а у l о r J., «Adwances Math.», 1972, v. 9, № 2, p. 183-252; [6] Энфло П., «Математика», 1974, т. 18, № 1, с. 146-55; [7] Шефор X., Топологические векторные пространства, пер. с англ., М., 1971; [8] Функциональный анализ, 2 изд., М., 1972 (Справоч. матем. б-ка); [9J Ломоносов В. И., «Функц. анализ и его прилож.», 1973, т. 7, № 3, с. 55-об; [10] Н i 1 b е r t Х D., Grundzijge einer allgemeinen Theoric der linearen Integralgleictmngen, Lpz.- В., 1912; N. Y., 1953; [11] Д а н ф о p д Н., Шварц Д ж., Линейные операторы. Общая теория, пер. с англ., М., 1962; [12] их же, Линейные операторы, пер. с англ., т. 2, М., 1966; [13] их же, Линейные операторы. Спектральные операторы, пер. с англ., М., 1974; [14] Г о х б е р г И. Ц., К р е й н М. Г., Теория вольтерровых операторов в гильбертовом пространстве и ее приложения, М., 1967; [15] Секефальви-Надь Б., Ф о я ш Ч., Гармонический анализ операторов в гильбертовом пространстве, пер. с франц., М., 1970; [16] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962. А. Я. Хелемский.