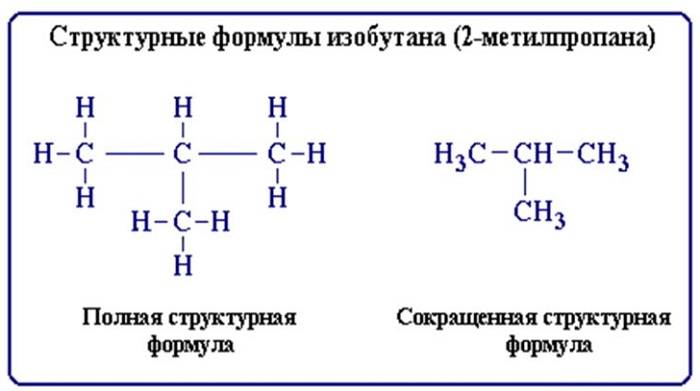
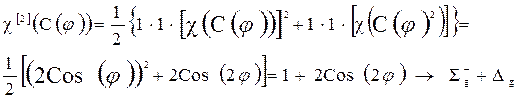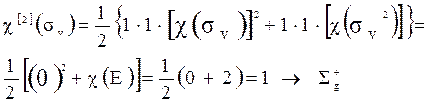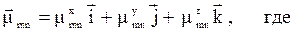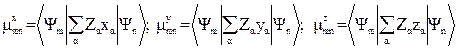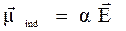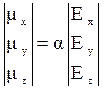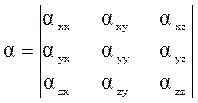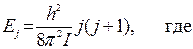что такое линейные молекулы
Что такое линейные молекулы
Одним из важнейших свойств ковалентной связи является её направленность. Она определяет пространственную структуру молекул. Если в молекуле имеется больше одной ковалентной связи, то двухэлектронные облака связей вступают во взаимодействие друг с другом. Представляя собой заряды одного знака, они отталкиваются друг от друга, стремясь занять такое положение в пространстве, когда их взаимное отталкивание будет минимальным. Если в первом приближении считать отталкивание всех облаков одинаковым, то в зависимости от числа взаимодействующих облаков (связей) наиболее выгодным расположением будет:
Это наиболее распространенные геометрические формы многоатомных молекул (рис. 8).
Часто в образовании связей участвуют различные электроны, например `s` и `p`—электроны. Казалось бы, образующиеся связи тоже должны быть неравноценными. Однако опыт показывает, что все связи одинаковы. Теоретическое обоснование этого факта было предложено Слейтером и Полингом, которые ввели понятие гибридизации атомных орбиталей. Они показали, что при участии в образовании связей нескольких различных орбиталей, незначительно отличающихся по энергии, можно заменить их тем же количеством одинаковых орбиталей, называемых гибридными. При этом орбитали смешиваются и выравниваются по энергии. Изменяется и первона-чальная форма электронных облаков: гибридные орбитали асимметричны и сильно вытянуты по одну сторону от ядра.
В этом соединении атому бериллия нужно образовать две связи с атомами хлора. Он переходит в возбужденное состояние и его электронная пара, находящаяся на `2s`-орбитали, распаривается:
Орбитали, занятые валентными электронами, гибридизуются по типу `sp`-гибридизации, в результате чего изменяется их первоначальная форма, они становятся одинаковыми как по форме, так и по энергии, и в таком состоянии способны образовывать более прочные связи за счёт наиболее полного перекрывания с `p`-орбиталями атомов хлора:
Однако нужно отметить, что для данного соединения употреблять термин «молекула» можно только тогда, когда хлорид бериллия находится в газообразном состоянии.
`3sp^2(«B»)+p(«Cl»)+p(«Cl»)+p(«Cl»)->3` ковалентные связи `»B»-«Cl»`.
Большая Энциклопедия Нефти и Газа
Линейная молекула
Линейные молекулы или конденсируются друг с другом с образованием длинных цепей, или циклизуются. [1]
Линейная молекула является частным случаем симметричного волчка. [2]
Линейная молекула может принимать в растворе вид рыхлого, имеющего форму эллипсоида клубка 3, что приводит к получению заниженных молекулярных весов при измерении вязкости. Роговин и полагает, что форма цепей в растворах главным образом зависит от химической природы высокомолекулярного вещества, от природы растворителя и от концентрации раствора. [3]
Линейные молекулы обладают симметрией D mh или С, в зависимости от того, имеют ли они плоскость симметрии, перпендикулярную к оси молекулы, или не имеют ее. [5]
Линейные молекулы имеют только две вращательные степени свободы, поскольку они обладают осевой симметрией, а вращение вокруг оси симметрии не приводит к изменению положения; аналогично атомы, обладающие сферической симметрией, не имеют вращательных степеней свободы. [6]
Линейная молекула имеет эффект Штарка второго порядка. [7]
Линейные молекулы и молекулы типа симметричного волчка имеют одну ось симметрии порядка выше второго. [8]
Линейная молекула имеет эффект Штарка второго порядка. [11]
Линейная молекула имеет всего две вращательные степени свободы, соответствующие двум углам Эйлера 0 и ф, необходимым для описания ориентации молекулярной оси ( т.е. оси г) в пространстве, и отсутствие третьего угла Эйлера вызывает определенные трудности. Здесь для читателя было бы полезно еще раз вернуться к гл. [12]
Линейные молекулы обладают только двумя вращательными степенями свободы, которые соответствуют вращению молекулы относительно двух взаимно перпендикулярных осей. Легко понять, почему вопрос о третьей вращательной степени свободы даже не возникает. В двухатомной молекуле атомы имеют шесть степеней свободы, три из которых соответствуют смещению молекулы как целого, одна ответственна за колебания атомов вдоль линии связи, и, таким образом, для описания вращения остаются только две степени свободы. Аналогичные рассуждения применимы к любой линейной молекуле. Величину й2 / 2 / обычно обозначают буквой В и называют вращательной постоянной молекулы. Важно отметить, что расстояние между вращательными уровнями уменьшается с увеличением момента инерции ( так как при этом уменьшается В) и что уровень / расположен на расстоянии 2В ( / 1) от следующего уровня. [14]
Линейные молекулы



В молекулах, как и в атомах, используется метод молекулярных орбиталей (МО) для представления волновой функции:
и неприводимое представление, к которому относится Yмол., определяется в виде произведения неприводимых представлений орбиталей:
В этом произведении нужно рассматривать только представления МО, заполненных одним электроном. Посколько двухкратнозанятые МО всегда дают полносимметричное представление. Т.о. симметрия молекул с замкнутыми оболочками, т.е. когда на каждой Мо находится по два электрона, всегда отвечает полносимметричному представлению точечной группы симметрии.
Симметрия электронного состояния систем с открытыми оболочками наиболее просто определяется в случае заполнения неспаренными электронами МО, соответствующих одномерным неприводимым представлениям. Здесь для определения симметрии состояния нужно перемножить только неприводимые представления, соответствующих МО.
Более сложный случай определения симметрии систем с открытыми оболочками – неспаренные электроны расположены на вырожденной МО. Например: молекула О2, у которой два электрона расположены на дважды вырожденной Мо (pg). Методика нахождения симметрии терма здесь такая же, как и в случае атомов. Представление записывается как:
| D¥h | Е | C(j) | C2 | sh | S(j) | i | sv |
| Г(О2) | 4cos 2 j | 4cos 2 j | |||||
| 2+2cos2j | 2+2cos2j |
Учёт спинов приводит к триплетным или синглетным состояниям.
Рассмотрим синглетное состояние.
Теория кристаллического поля.
Это простейшая теоретическая модель используемая обычно для описания электронных спектров переходных металлов. По сути, это просто модель возмущения атомных орбиталей центрального атома электростатическим полем лигандов. Основная идея её состоит в отображении орбитальных представлений центрального атома (Rh(3)) на соответствующую группу точечной симметрии комплекса. Эта модель является достаточно грубой и т.о. позволяет описать наиболее важные характеристики спектров этих молекул. Комплексы с переходными металлами обладают частично-заполненной d-оболочкой, поэтому, необходимо рассматривать отображение представления d-орбиталей в группе Rh(3) на соответствующую точечную группу. Этим представлением является Dg(2).
[Далее в задачах рассмотреть молекулы MF3(D3h), MF4(Td), MF5(D3h). Система d-уровней. Определить термы MF3(M=Ti, V, Gr, Mn, Fe, Co.]
Правила отбора.
В соответствии с положениями квантовой механики любая наблюдаемая величина может быть вычислена в виде интеграла:
Если величина А – скаляр, то очевидно она не должна изменяться при всех операциях симметрии. Т.е. А должна быть инвариантна по отношению ко всем операциям симметрии. Это возможно, если интеграл áYi½Â½Yj ñ преобразуется по полносимметричному представлению группы. Если это условие не выполняется, то интеграл равен нулю. Таким образом, если через Гi, Г и Гj обозначить неприводимые представления, по которым преобразуются Yi,  и Yj, то представление по которому преобразуется интеграл будет вычисляться как
Представление Г содержит полносимметричное неприводимое представление в том случае, если произведение любых двух представлений содержит третье:
Именно на этом свойстве основаны правила отбора, позволяющие исходя из симметрии молекулы определить наблюдаемые полосы в электронных, колебательные и вращательных спектрах. Переходы между различными энергетическими уровнями связана с поглощением или испусканием кванта энергии. Интенсивность перехода пропорциональна величине дипольного момента перехода:
mmn, где 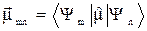
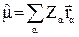
Компоненты дипольного момента – проекции на осо координат – скалярные величины. Следовательно, для того, чтобы они отличались от нуля необходимо выполнение условия:
Проникающие в вещество излучение может вызывать явления, отличные от поглощения или испускания, но сопровождающиеся изменением энергии системы. Это явление рассеяния света (спектры комбинационного рассеяния или рамановские). В этом случае в системе индуцируется переменный диполь. Величина этого индуцированного диполя пропорциональна величине напряженности падающей электромагнитной волны:
Используя декартово представление векторов это выражение можно записать как:
Правила отбора в электронном спектре.
Т.о. DJ = J’-J = ±1 при J=0 и
DJ = J’-J = 0, ±1 при J¹0.
В молекулах правила отбора для электронных переходов аналогичны атомным. Т.е. при DS=0 необходимо, чтобы выполнялось условие:
Однако нужно иметь в виду, что присутствие в молекуле тяжелых атомов может нарушить правило отбора по DS.
Вращательные спектры. В приближении жесткого ротатора энергия вращательных уровней определяется по формуле:
I – момент инерции, j – вращательное квантовое число. Волновые функции, вычисленные в приближении жесткого ротатора, имеют вид подобный волновым функциям, описывающим электронные состояния атома водорода. Поэтому и правила отбора аналогичны полученным ранее для электронных переходом в атомах. При этом, однако, нужно иметь в виду, что изменение вращательного квантового числа Dj=0 не имеет физического смысла (энергия не изменяется). Т.о. единственным имеющим физический смысл ограничением будет: Dj=±1.
В модели жесткого ротатора внутренние координаты молекулы не изменяются. Следовательно, постоянный дипольный момент молекулы так же не изменяется. В случае отсутствия у молекулы постоянного дипольного момента вращетельный спектр можно наблюдать только в спектрах комбинационного рассеяния.
Колебательные спектры. Колебания в молекулах представляют собой смещения ядер от положения равновесия. При равновесном положении конфигурация молекулы остается неизменной при любой операции симметрии соответствующей точечной группы. Т.о. волновая функция описывающая колебание молекулы на нулевом колебательном уровне, соответствующем неискаженной равновесной геометрии, преобразуется всегда по полносимметричному представлению. В то время как волновая функция в колебательно возбужденном состоянии преобразется по некому неприводимому представлению Г(Yn=n’) часто отличному от полносимметричного. Тогда произведение представлений волновых функций, отвечающих нулевому и возбужденному колебательным состояниям, равно:
Т.о переход из нулевого состояния в возбужденное будет виден в колебательном спектре поглощения или испускания если:
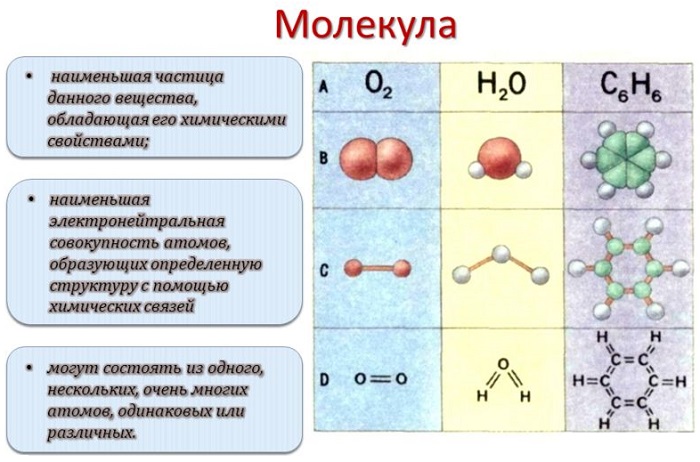
Одним из основополагающих понятий современной науки является понятие молекулы. Его введение европейскими учеными в 1860 г. дало толчок к развитию не только химии и физики, но и других естественных наук.
Молекулой, в наиболее общем определении, называется частица, образованная из нескольких (двух или более) атомов, объединенных между собой ковалентными связями. Она не имеет электрического заряда, все электроны в её составе имеют пару.
Молекулы, несущие заряд, называются ионами, неспаренные электроны – радикалами. Качественный и количественный состав их стабилен. Количество ядер атомов, электронов и их взаимное расположение позволяют отличать молекулы разных веществ друг от друга.
Что такое молекула в физике
В физике этим понятием оперируют при изучении свойств разных сред (газы, жидкости) и твердых тел.
Также их свойствами объясняются явления диффузии, теплопроводности и вязкость веществ.
Что такое молекула в химии
Учение о молекулах для химической науки является одним из самых главных. Именно химические исследования дали важнейшие сведения о составе и свойствах этой мельчайшей единицы вещества.
При прохождении химического превращения молекулы обмениваются атомами, распадаются. Поэтому знания о строении и состоянии этих частиц лежат в основе изучения химии веществ и их превращений.
На основании знаний о проходящей химической реакции можно предсказать строение молекул веществ, в ней участвующих. Противоположное заключение тоже будет верным: на основании сведений о строении молекулы вещества реально предсказать его поведение во время химической реакции.
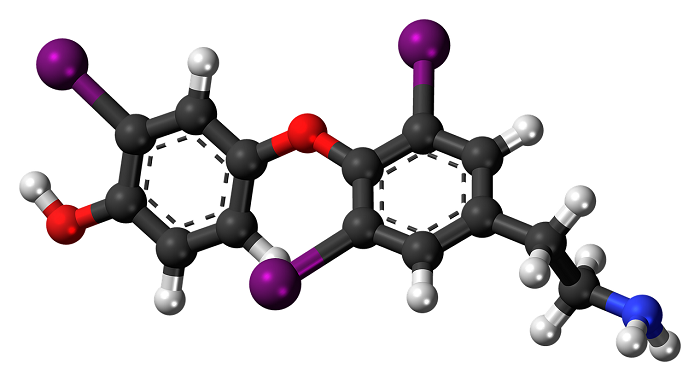
Строение молекулы
Понятие о строении включает геометрическую структуру и распределение электронной плотности.
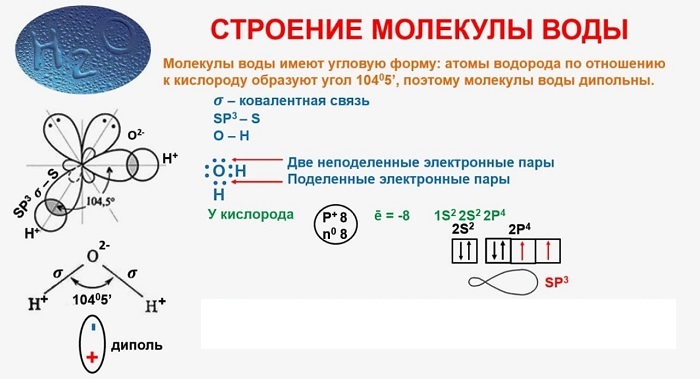
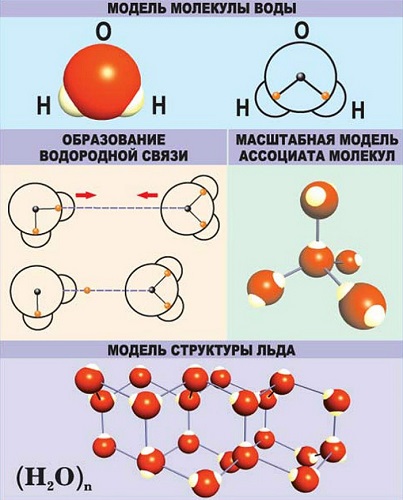
В качестве примера рассмотрим строение наименьшей частицы воды.
Существует несколько способов взаимодействия атомов. Основным способом являются химические связи, благодаря им поддерживается стабильное существование молекул. Прочие (неосновные) взаимодействия происходят между теми атомами, которые не связаны непосредственно.
Виды химической связи:
Водородная — основана на способности атома водорода образовывать дополнительную связь при смещении от него электронной плотности.
Связи характеризуются следующими показателями:
длина – степень удаления друг от друга ядер атомов, образовавших связь;
энергия – сила, прилагаемая для разрушения связи;
полярность – смещение электронного облака к одному из атомов;
порядок или кратность – количество пар электронов, образовавших связь.
Строение молекул условно отражается структурными формулами. Основные взаимодействия атомов, при составлении таких формул, отображается черточками. В таких формулах связи образуют неразрывную цепь и иллюстрируют валентности образовавших их элементов (атомов).
Структурные формулы также отражают то, как выглядит молекула (линейная, циклическая, наличие радикалов и т. д.).
Масса (размер) молекулы
В зависимости о количества ядер атомов, входящих в их состав, можно выделить молекулы двухатомные, трехатомные и т. д.
В том случае, если количество атомов велико, молекула носит название макромолекулы.
Путем сложения масс атомов, входящих в состав частицы, можно определить молекулярную массу. В зависимости от её величины, все вещества делят на высоко- и низкомолекулярные.
Свойства молекулы
Современная наука выделяет следующие свойства молекул:
Знания о свойствах и строении молекул являются основополагающими для развития теоретических и прикладных наук и играют важную роль в жизни человека.
молекула
Представление о M. возникло в 18 в. и с развитием в 19 в. кинетич. теории газов и становлением термодинамики получило широкое распространение. Прямое эксперим. подтверждение существования M. провёл Ж. Перрон (J. Perrin) при изучении броуновского движения (1906).
Молекулярные вещества в газовой и жидкой фазах и в молекулярных кристаллах сохраняют индивидуальность. В расплавах и ионных кристаллах M., как правило, утрачивают индивидуальность, т. к. каждый атом в них связан с большим числом окружающих его атомов.
Такие системы неустойчивы и распадаются под внеш. воздействием.
В M. между валентными электронами в основном состоянии преобладает обменное взаимодействие, к-рое выстраивает спины электронов антипараллельно, поэтому осн. электронное состояние большинства M. синглетное, M. диамагнитна. Свободные радикалы обычно парамагнитны.
0,01 
1° в валентных углах) обычно обусловлены различием колебат. поправок к структурным параметрам. Кроме того, низкосимметричные изотопич. модификации неполярных M. могут быть слабо полярными с дипольным моментом ок. 0,01 дебая.
Полные электронно-колебательно-вращательныо (рови-бронные) уровни энергии M. классифицируют по неприводимым представлениям (типам симметрии) группы симметрии молекулы. Разделение полного движения на отд. виды дает возможность ввести приближённые квантовые числа для классификации уровней M. В большинстве случаев эти числа связаны с собств. значениями квадратов и z-проекций соответствующих угл. моментов. В спектроскопии двухатомных M. используются угл. моменты и их квантовые числа, приведённые в табл.
В простейшем приближении каждому нормальному колебанию M. v k сопоставляется гармонический осциллятор с энергией
Вращательные уровни энергии M. в 1 S— состоянии. Вращат. уровни M. качественно описываются в рамках модели жёсткого волчка. Вращат. энергия жёсткой (т. е. колебания её атомных ядер незначительны) двухатомной M. в 1 S-состоянии
и сплюснутые, для к-рых
Сумма К а + К с равна J (при чётном J)или J + 1 (при нечётном J). Асимметрия волчка характеризуется параметром:
Модель жёсткого волчка является грубым приближением к реальной M. Реально M. при вращении искажается, и такое центробежное искажение даёт существенный вклад в её энергию. В случае двухатомной M. основная (квартичная) центробежная поправка к (3) равна
сдвигает уровни, а вторая, зависящая от симметрии M., может приводить к снятию вырождения уровней по знаку К. Для асимметричных волчков центробежная поправка к энергии определяется только численно. Константы квартичного центробежного искажения зависят от квадратичных членов разложения потенциальной поверхности и используются для определения гармонич. силовых постоянных M. Обычно из вращат. спектров M. определяются также константы центробежных поправок более высокого порядка (секстичные, октичные и др.), к-рые содержат информацию о константах энгармонизма M.
Колебательные уровни энергии M. В гармонич. приближении энергия колебат. уровней M. определяется суммой выражений типа (1) по всем нормальным колебаниям, к-рые возбуждены в данном состоянии:
Электронные уровни M. можно получить также из уровней разъединённых атомов (р. а.) или групп зто-мов по векторной модели. При этом квантовое число L получается алгебраич. сложением проекций M Li орбитальных моментов всех атомов,
а полный электронный спин M. получается как векторная сумма спинов атомов
Модели о. а. и р. а. позволяют определить кол-во электронных уровней разл. типов симметрии, но не дают надёжных сведений относительно их энергии. Более полную информацию о расположении уровней и их устойчивости дают молекулярные орбитали.
Электронные уровни энергии расщепляются за счёт спин-орбитального взаимодействия на т. н. мультиплет-иые уровни (см. Мультиплетность). В случае нормальной связи это расщепление равно:
Ядерная сверхтонкая структура энергии уровней M.
Обычно квадрупольное взаимодействие даёт осн. вклад в CTC, но оно имеет место только для ядер со спином l > 1 / 2 (напр., D, 14 N, Cl, Br, I). В простейшем случае одиночного квадрупольного ядра в двухатомной M. энергия квадрупольного взаимодействия описывается ф-лой
Квадрупольная CTC обычно наблюдается в спектрах высокого разрешения. Спин-вращательные и спин-спиновые взаимодействия дают небольшой вклад в CTC и имеют место для всех ядер со спином I >= 1 / 2 (I = 1 / 2 для H, F и др.). Расщепления вращат. уровней за счёт этих взаимодействий составляют обычно не более 100 кГц и наблюдаются только на уникальных установках (пучковые мазеры, электрич. резонанс в пучке и Др.). Эксперим. данные по константам квадруполь-ной связи и спин-вращательного взаимодействия дают ценную информацию об электронном строении M., а константы спин-спиновых взаимодействий зависят только от гсом. параметров M.
Все физ. и хим. свойства M. так или иначе связаны с системой уровней энергии M. и с переходами между ними под действием внеш. возмущений.
Электрические свойства M. Молекула как система положит. и отрицат. зарядов характеризуется опре-дел. расположением зарядов, т. с. обладает электрич. дипольным, квадрупольным и т. д. моментами. Определяет электрич. свойства M. её дипольный момент m:
Магнитные свойства M. В состоянии с орбитальным моментом L электрона M. имеет орбитальный магн. момент
T. к. M z всегда относится к полносимметричному типу симметрии и [Г 2 ] всегда содержит полносимметричный тип, условие (30) фактически не ограничивает класс состояний, в к-рых H имеет диагональные элементы. T. о., расщепление уровней энергии во внеш. магн. поле (Зеемана эффект)происходит для всех M. уже в первом приближении, т. е. наличие линейного по нолю эффекта Зеемана ничем не ограничено. Величина линейного зеемановского расщепления для жёсткого асимметричного волчка даётся ф-лой:
ср. значение 2 a > определяют численно. Для симметричного волчка
а для линейной M. g J = g, т. е. не зависит от J. Обычно расщепления уровней энергии за счёт вращат. эффекта Зеемана малы и для их точного измерения используют магн. поля
По величине зеемановского расщепления уровней энергии определяются вращат. g-факторы и компоненты тензора c, а из них вычисляются электрич. квадру-польные моменты M. по ф-лам:
а электронный g-фактор
Полное число M. в данном объёме пропорц. суммe величин Q n по всем состояниям M., т. е.
Величина Q наз. статистической суммой или суммой по состояниям, через неё могут быть выражены все термодинамич. ф-ции идеального газа, причём учитываются все степени свободы M., включая и её поступат. движение. Если не учитывать взаимодействие между видами внутр. движений M., то величину Q можно представить в виде произведения поступательной (Q t ), вращательной (Q r ), колебательной (Q u )и электронной (Q e )статистич. сумм:
Статистич. сумма поступат. движения M. для объёма газа V и темп-ры T равна
T. о., если известны частоты нормальных колебаний и вращат. постоянные M., то можно найти полную статистич. сумму Q, а затем вычислить термодинамич. ф-ции газа. В частности, теплоёмкость С р одного моля газа при пост. давлении определяется по ф-ле