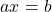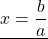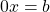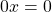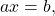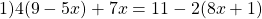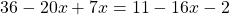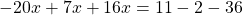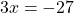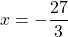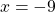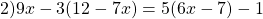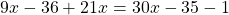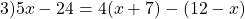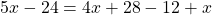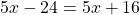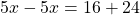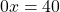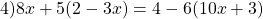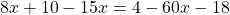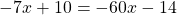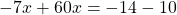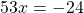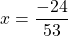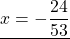что такое линейное уравнение 7 класс
Решение линейных уравнений 7 класс
Для решения линейных уравнений используют два основных правила (свойства).
Свойство № 1
или
правило переноса
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число « 3 » из левой части уравнения в правую.
Так как в левой части уравнения у числа « 3 » был знак « + », значит в правую часть уравнения « 3 » перенесется со знаком « − ».
Полученное числовое значение « x = 2 » называют корнем уравнения.
Не забывайте после решения любого уравнения записывать ответ.
Рассмотрим другое уравнение.
По правилу переноса перенесем « 4x » из правой части уравнения в левую, поменяв знак на противоположный.
Несмотря на то, что перед « 4x » не стоит никакого знака, мы понимаем, что перед « 4x » стоит знак « + ».
Теперь приведем подобные и решим уравнение до конца.
Свойство № 2
или
правило деления
Но нельзя делить на неизвестное!
Разберемся на примере, как использовать правило деления при решении линейных уравнений.
Число « 4 », которое стоит при « x », называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение.
Чтобы решить уравнение необходимо сделать так, чтобы при « x » стоял коэффициент « 1 ».
Давайте зададим себе вопрос: «На что нужно разделить « 4 », чтобы
получить « 1 »?». Ответ очевиден, нужно разделить на « 4 ».
Используем сокращение дробей и решим линейное уравнение до конца.
Как решить уравнение, если « x » отрицательное
Часто в уравнениях встречается ситуация, когда при « x » стоит отрицательный коэффициент. Как, например, в уравнении ниже.
Чтобы решить такое уравнение, снова зададим себе вопрос: «На что нужно разделить « −2 », чтобы получить « 1 »?». Нужно разделить на « −2 ».
При делении на отрицательное число помните про правило знаков.
Примеры решения линейных уравнений
Рассмотрим другие примеры решения линейных уравнений. Обычно для решения уравнений нужно применять оба свойства (правило переноса и правило деления).
Что такое линейное уравнение
Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?
В курсе алгебры 7 класса линейное уравнение определяется следующим образом.
Определение.
Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.
Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.
Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:
Количество корней линейного уравнения зависит от значения a (коэффициента перед x).
При a≠0 линейное уравнение имеет единственное решение.
Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:
Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).
В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).
При a=0, b≠0 линейное уравнение
При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.
При a=0, b=0 линейное уравнение
имеет бесконечное множество решений.
При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.
Возможные решения линейных уравнений можно изобразить в виде схемы.
Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.
Решение многих уравнений сводится к решению линейных уравнений.
Линейные уравнения 7 класс
Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида
где a и b — числа, x — переменная.
Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).
Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.
Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:
Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:
Обе части уравнения делим на число, стоящее перед иксом:
Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:
(Обратите внимание: хотя сумма слагаемых с переменной равна нулю, результат записываем не как 0, а как 0x).
Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.
Ответ: x — любое число.
Можно сначала привести подобные слагаемые, чтобы упростить уравнение:
а уже потом перенести: неизвестные — в одну сторону, известные — в другую:
Это уравнение не имеет корней.
Приводим подобные слагаемые:
Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.
14 комментариев
А в третьем уравнении ошибку вы допустилтхи. Перенесли неправильно 60х. Ответ должен быть х=24/53.
Спасибо, Маша! Ошибка исправлена.
Полли, мы обе части уравнения делим на число, стоящее перед иксом: 3х=-27; х=-27:3, то есть знаки делимого и делителя разные, поэтому ответ со знаком «-«.
Да админ прав, делаем проверку 3X(-9)=-27
Х=-9 Потаму что если в делитиле и в знаментаиле имеются как вы сказали знаки минуса оно как в умножении не меняется.
Нет
Т.к. — делёный на + будет —
Спасибо за понятное изложение темы. Перерыв десяток сайтов и только на вашем нашел ответ на вопрос » как решать линейные уравнения «. Вам + 5 в карму:)
mne tut vse ponjatno. u menja problema s sostavleniem uravnenij/kak zapisatj zada4u matemati4eskim jazikom/ kombinatorika!
Линейные уравнения
Примеры линейных уравнений:
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.
Примеры решения линейных уравнений:
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b :
Для начала раскроем скобки:
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
Это уравнение не является линейным уравнением.
Особые случаи (встречаются редко, но знать их полезно).
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
Задания для самостоятельного решения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
2 − 3 ( 2 x + 2 ) = 5 − 4 x
Переносим иксы влево, числа вправо:
x = 9 − 2 = − 9 2 = − 4,5
№2. При каком значении x значения выражений 7 x − 2 и 3 x + 6 равны?
Решение:
Приравниваем эти два выражения:
№3. Решите уравнение ( − 5 x + 3 ) ( − x + 6 ) = 0.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Чтобы найти все корни данного уравнения, надо приравнять каждый множитель к нулю и оба корня взять в ответ.
( − 5 x + 3 ) ( − x + 6 ) = 0 ⇔ [ − 5 x + 3 = 0 − x + 6 = 0 ⇒ [ − 5 x = − 3 ; − x = − 6 ; ⇒ [ x = − 3 − 5 = 3 5 = 0,6 x = − 6 − 1 = 6 1 = 6
В задании указано, что в ответ надо записать корни в порядке возрастания 0,6 6.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
Раскроем квадраты, используя ФСУ (формулы сокращенного умножения):
x 2 − 2 ⋅ x ⋅ 4 + 4 2 + x 2 + 2 ⋅ x ⋅ 9 + 9 2 − 2 x 2 = 0
Замечаем, что x 2 сокращается:
x 2 − 8 x + 4 2 + x 2 + 18 x + 9 2 − 2 x 2 = 0
− 8 x + 18 x + 16 + 81 = 0
Решение:
Раскроем скобки, используя ФСУ.
( x + 10 ) 2 = ( 5 − x ) 2
x 2 + 2 ⋅ x ⋅ 10 + 10 2 = 5 2 − 2 ⋅ 5 ⋅ x + x 2
x 2 + 20 x + 100 = 25 − 10 x + x 2
x 2 + 20 x + 100 − x 2 + 10 x − 25 = 0
Решение:
Решение линейных уравнений с одной переменной
В данной статье рассмотрим принцип решения таких уравнений как линейные уравнения. Запишем определение этих уравнений, зададим общий вид. Разберем все условия нахождения решений линейных уравнений, используя, в том числе, практические примеры.
Обратим внимание, что материал ниже содержит информацию по линейным уравнениям с одной переменной. Линейные уравнения с двумя переменными рассматриваются в отдельной статье.
Что такое линейное уравнение
Такая формулировка использована в учебнике алгебры ( 7 класс) Ю.Н.Макарычева.
Примерами линейных уравнений будут:
3 · x = 11 (уравнение с одной переменной x при а = 5 и b = 10 );
В различных учебных материалах могут встречаться разные определения. К примеру, Виленкин Н.Я. к линейным относит также те уравнения, которые возможно преобразовать в вид a · x = b при помощи переноса слагаемых из одной части в другую со сменой знака и приведения подобных слагаемых. Если следовать такой трактовке, уравнение 5 · x = 2 · x + 6 – также линейное.
А вот учебник алгебры ( 7 класс) Мордковича А.Г. задает такое описание:
Примером линейных уравнений подобного вида могут быть:
Принцип решения линейных уравнений
Рассмотрим, как определить, будет ли заданное линейное уравнение иметь корни и, если да, то сколько и как их определить.
Дадим пояснение. Нам известно, что в процессе решения уравнения возможно осуществлять преобразование заданного уравнения в равносильное ему, а значит имеющее те же корни, что исходное уравнение, или также не имеющее корней. Мы можем производить следующие равносильные преобразования:
Все приведенные рассуждения дают нам возможность записать алгоритм, дающий возможность найти решение любого линейного уравнения:
Собственно, описанная последовательность действий и есть ответ на вопрос, как находить решение линейного уравнения.
Примеры решения линейных уравнений
Решение
Ответ: x – любое число.