что такое квантовая теория поля
Что такое квантовое поле?
В физике мы регулярно говорим о полях: магнитном поле, электрическом поле, гравитационном поле. В более общем плане можно даже говорить о «квантовых полях», которые используются в квантовой физике для описания мира.
В классической физике, или ньютоновской физике, мы говорим о частицах. Протоны, электроны, все это частицы. Их можно рассматривать как маленькие шарики элементарной материи, из которых состоят все материалы, которые мы видим.
Эта модель хорошо работает на многих вещах, но и она не все объясняет. Она не объясняет, например, как частицы могут мешать друг другу.
Считается, что эти элементы обладают двойственностью волны-частицы, хотя это не удобная концепция для работы: если считать, что это частица, часть теории не сработает. И наоборот, если нужно рассматривать частицу как волну, то могут быть применены только определенные уравнения.
В физике это недопустимо: уравнение должно применяться в любое время и в любом месте.
Понятие квантовых полей
Помимо проблемы физической реальности элементарных частиц, необходимо изучить, как они взаимодействуют.
Понятие поля в математике
Возьмите двух- или трехмерный ориентир что угодно. Визуализируйте точку в этом ориентире, любую. Сопоставьте с этой точкой значение, любое. Сделайте то же самое для другого пункта, затем другого. Фактически, с каждой точкой в этой системе координат сопоставьте значение. Когда вы это сделали, у вас есть поле.
Поле представляет собой ориентир, к которому привязано значение для каждой точки.
Например: возьмите комнату, в которой вы находитесь, затем поместите начало координат (0; 0; 0) в один из углов. Теперь у каждого места в комнате есть координаты. Наконец, для каждого места в комнате укажите температуру в этой точке. Затем мы получаем карту температуры в вашей комнате: математически эта карта представляет собой поле: поле температуры.
К одной и той же точке могут быть привязаны несколько значений. В нашем примере, помимо температуры, можно связать атмосферное давление, влажность, чистоту воздуха, скорость выбросов CO2 и т.д. Тогда у нас есть ориентир с множеством полей.
У нас также может быть векторное поле, что позволяет связать вектор с любой точкой в пространстве. Например, если мы свяжем скорость ветра в этой точке с каждой точкой в пространстве, мы получим векторное поле.
Эти различные поля могут быть связаны: таким образом, вектор скорости или даже влажность в точке будут зависеть от давления и температуры воздуха в окружающих точках.
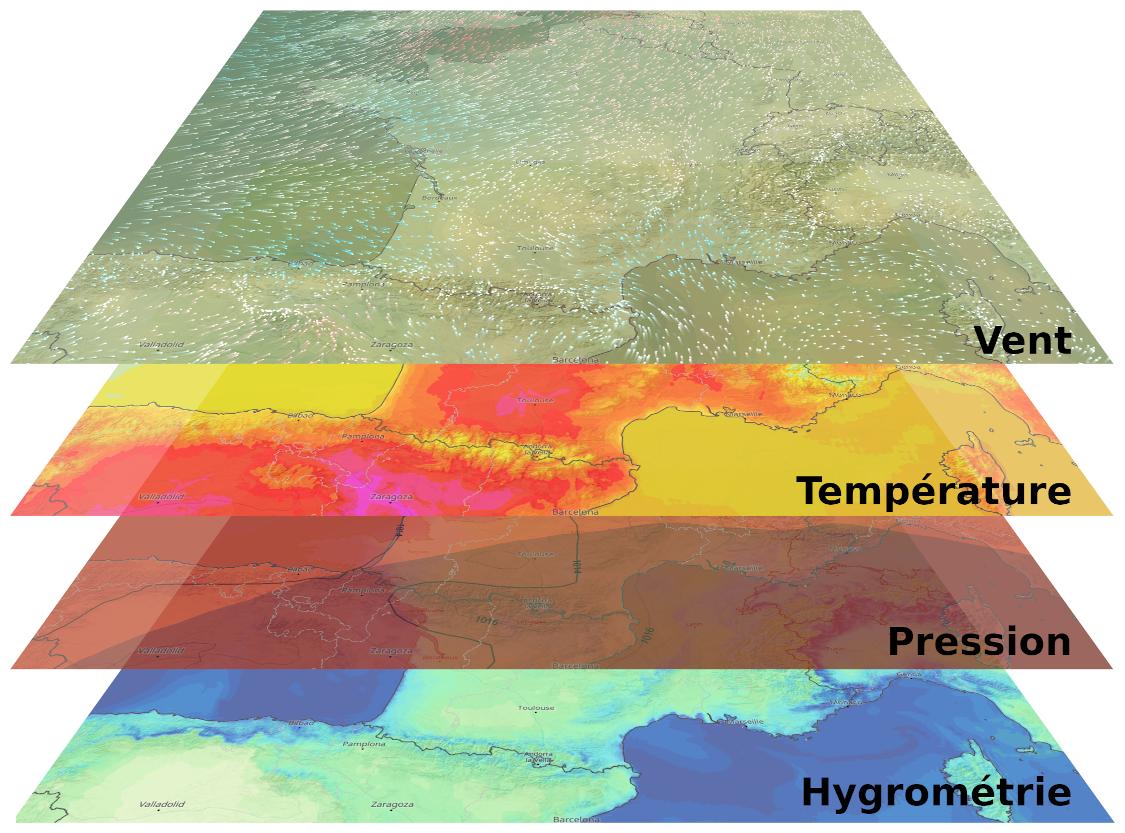
Эта работа является то, что делается в метеорологии: с помощью физических показаний (температура, давление, относительная влажность) можно определить, будет ли ветер, в каком направлении, или предсказать изменения относительной влажности, дождя, короче говоря, прогноз погоды в ближайшие часы или дни.
Реальная погода в том или ином месте может быть разбита на несколько параметров, смоделированных по полям: ветер, температура, давление, влажность и т. д.
Мы также можем ассоциировать тензоры с каждой точкой (более общий объект, чем скаляры и векторы).
Использование полей в физике
Теперь, если вы зажжете свечу в одном месте, температура будет очень высокой там, где находится пламя. Это будет учтено в температурном поле со значительно более высокими значениями температуры в координатах, где находится пламя свечи.
И наоборот, если вы посмотрите на температурную карту комнаты и увидите, что в определенном месте температура значительно повышается, вы можете сделать вывод, что кто-то зажег там свечу.
Точно так же, если вы видите, что эта температурная «аномалия» меняет координаты со временем, вы можете сделать вывод, что кто-то перемещает свечу по комнате.
Если эта температурная аномалия внезапно исчезает, значит, свеча погасла.
Это очень простой пример для изучения поля в соответствии с физическим параметром.
Вместо температуры мы можем взять значение электрического заряда в этом месте. Если мы поместим себя в абсолютный вакуум, мы заметим, что электрическое поле и магнитное поле равны нулю во всех точках. Если мы сейчас отправим фотон через вакуум, мы заметим возмущение, которое распространяется в электрическом и магнитном полях. Это возмущение соответствует фотону, пересекающему вакуум.
Концепция квантовых полей в квантовой физике
Выше, в нашем примере вакуума, через который проходит фотон, мы рассматриваем частицу, фотон, и моделируем его возмущением в электромагнитном поле.
Но что, если бы мы поступили наоборот? Если бы мы считали, что фотон в своем наиболее фундаментальном описании был только возмущением полей, и что мы моделировали это возмущение как частицу?
В квантовой физике в квантовой теории поля это то, что мы делаем: рассматриваем частицы уже не как маленькие конденсированные шарики материи, а как возмущения, присутствующие на поверхности квантового поля. В таком случае «маленькая частица» представляет собой упрощенное описание, которое предполагается более интуитивным.
В рамках квантовой теории поля Вселенная заполнена различными полями: электрическими, магнитными, гравитационными, и частице соответствует возбуждение на этих разных полях.
Например:
В квантовой физике мы работаем с такими вещами. Мы больше не говорим о частицах как о шарах материи, а как о точечных волнах: известных пакетах волн, возникающих через одно или несколько квантовых полей и реагирующих с ними.
В итоге
Подводя итог, мы можем видеть Вселенную как холст, заполненный разными слоями, соответствующими различным квантовым полям: электрическому полю, магнитному полю, гравитационному полю и т.д.
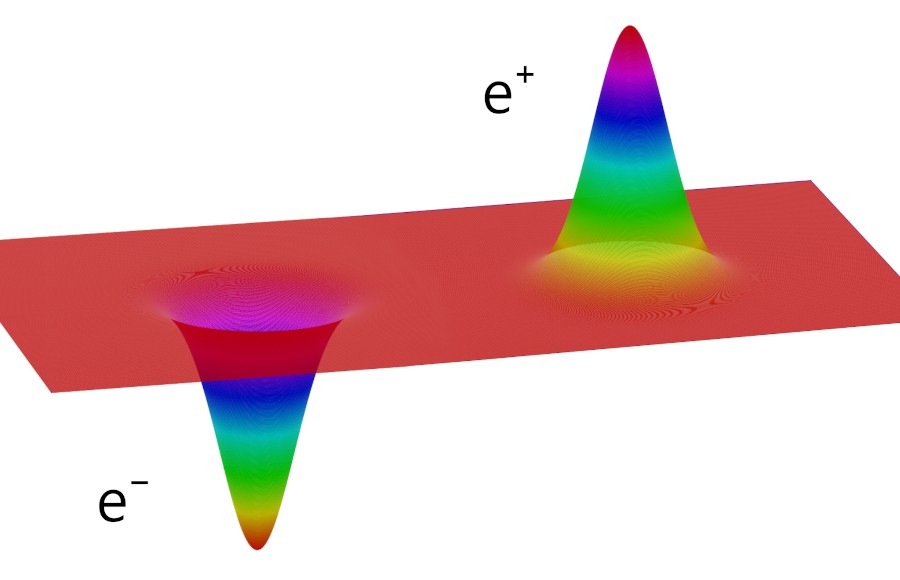
Поэтому каждая точка в этом пространстве характеризуется значением, соответствующим напряженности электрического, магнитного, гравитационного и т.д. поля в этой точке:
Схема электрического поля для электрона (отрицательного) и позитрона (положительного)
Данная частица, которая войдет в это пространство, изменит различные поля в соответствии со своими физическими параметрами (электрический заряд, масса…). Анализируя значения этих полей в данном месте, мы можем определить, какая частица только что пересекла это пространство.
Это то, что происходит в ускорителях частиц: наши теоретические модели предсказывают появление или существование определенных частиц, а целью является их фактическое обнаружение, для того, чтобы подтвердить теоретическую модель.
Взаимодействия между частицами соответствуют действию возмущения поля на другие возмущения того же поля или других полей, например, помехи.
Каждое взаимодействие одной частицы с другой соответствует передаче энергии от одного поля к другому. Возмущение электрического поля может передаваться магнитному, гравитационному и т.д. Когда пара частица-античастица аннигилирует, масса может быть преобразована в фотон, а значит, в электромагнитную энергию.
В целом энергия сохраняется, но она может переходить из одного поля в другое.
«В основе мироздания лежит понятие красоты»: физик объясняет квантовую теорию поля
Sasha Kononenko
Квантовая механика, не говоря уже о квантовой теории поля, имеет репутацию странной, пугающей и контринтуитивной науки. В научном сообществе есть те, кто по сей день ее не признает. Однако же квантовая теория поля — единственная подтвержденная экспериментом теория, способная объяснить взаимодействие микрочастиц при низких энергиях. Почему это важно? Андрей Ковтун, студент МФТИ и сотрудник кафедры фундаментальных взаимодействий, рассказывает, как с помощью этой теории добраться до главных законов природы или придумать их самим.
Андрей Ковтун
Как известно, все естественные науки подчиняются определенной иерархии. Например, биология и химия имеют физические основания. И если смотреть на мир через лупу и каждый раз увеличивать ее силу, проводя таким образом редукцию знания, мы потихоньку придем к квантовой теории поля. Это наука, которая описывает свойства и взаимодействия самых маленьких крупиц матери, из которых мы состоим, — частиц, которые принято называть элементарными. Некоторые из них — такие, как, например, электрон — существуют сами по себе, другие же объединяются и образуют составные частицы. Всем известные протоны и нейтроны как раз являются таковыми — они состоят из кварков. А вот сами по себе кварки уже элементарны. Так вот задача физиков — понять и вывести все свойства этих частиц и ответить на вопрос, есть ли еще что-то, что лежит глубже в иерархии фундаментальных физических законов.
Наша реальность — полевая, она состоит из полей, а мы лишь элементарные возбуждения этих полей
Для радикальных ученых конечная цель — полная редукция знаний о мире, для менее радикальных — более глубинное проникновение в тонкости микромира или сверхмикромира. Но как это возможно, если мы имеем дело лишь с частицами? Ответ очень прост. Мы просто берем и сталкиваем их, в прямом смысле разбиваем друг о друга — как дети, которые, желая посмотреть устройство какой-нибудь занятной вещицы, просто бросают ее на пол, а потом изучают осколки. Также и мы сталкиваем частицы, а потом смотрим, какие новые частицы получаются при столкновении, а какие распадаются после продолжительного путешествия в гордом одиночестве. Все эти процессы в квантовой теории описываются так называемыми вероятностями распада и рассеяния. Расчетами этих величин и занимается квантовая теория поля. Но не только ими.
Векторы вместо координат и скоростей
Основное отличие квантовой механики — в том, что мы больше не будем описывать физические тела с помощью координат и скоростей. Основное понятие в квантовой механике — это вектор состояния. Это шкатулка с информацией о физической системе, которую мы изучаем. Причем я использую слово «система», потому что вектор состояния — это штука, которая может описывать состояние как электрона, так и бабушки, лузгающей семечки на скамейке. То есть это понятие имеет очень широкий круг охвата. И мы хотим найти все векторы состояния, которые содержали бы в себе всю необходимую нам информацию об изучаемом объекте.
Далее естественно задаться вопросом «А как же нам эти векторы найти, а потом извлечь из них то, что хочется?». Здесь нам на помощь приходит следующее важное понятие квантовой механики — оператор. Это правило, по которому одному вектору состояния ставится в соответствие другой. Операторы должны обладать определенными свойствами, и некоторые из них (но не все) извлекают информацию из векторов состояния о нужных нам физических величинах. Такие операторы называются операторами физических величин.
Измерить то, что трудно измерить
Квантовая механика последовательно решает две задачи — стационарную и эволюционную, причем по очереди. Суть стационарной задачи состоит в том, чтобы определить все возможные векторы состояния, которые могут описывать физическую систему в данный момент времени. Такие векторы являются так называемыми собственными векторами операторов физических величин. Определив их в начальный момент, интересно проследить, как они будут эволюционировать, то есть меняться со временем.
Мюон — неустойчивая элементарная частица с отрицательным электрическим зарядом и спином 1⁄2. Антимюон — античастица с квантовыми числами (в том числе зарядом) противоположного знака, но с равной массой и спином.
Посмотрим на эволюционную задачу с точки зрения теории элементарных частиц. Пусть мы хотим столкнуть электрон и его партнера — позитрон. Другими словами, у нас есть вектор состояния-1, который описывает электрон-позитронную пару с определенными импульсами в начальном состоянии. А потом мы хотим узнать, с какой вероятностью после столкновения электрона и позитрона родятся мюон и антимюон. То есть система будет описываться вектором состояния, который содержит информацию про мюон и его антипартнера тоже с определенными импульсами в конечном состоянии. Вот вам и эволюционная задача — мы хотим узнать, с какой вероятностью наша квантовая система перескочит из одного состояния в другое.
Образование пары позитрон — электрон © iStock
Пусть мы также решаем задачу о переходе физической системы из состояния-1 в состояние-2. Допустим, у вас есть шарик. Он хочет попасть из точки A в точку B, и существует множество мыслимых путей, по которым он мог бы совершить это путешествие. Но повседневный опыт показывает, что если вы кидаете шарик под определенным углом и с определенной скоростью, то у него есть только один реальный путь. Квантовая же механика утверждает другое. Она говорит, что шарик путешествует одновременно по всем этим траекториям. Каждая из траекторий вносит свой (больший или меньший) вклад в вероятность перехода из одной точки в другую.
Квантовая теория поля называется так потому, что она описывает не частицы сами по себе, а некоторые более общие сущности, которые называются полями. Частицы же в квантовой теории поля являются элементарными переносчиками полей. Представьте воды мирового океана. Пусть наш океан спокоен, на его поверхности ничего не бурлит, нет волн, пены и так далее. Наш океан есть поле. А теперь представьте уединенную волну — только один гребень волны в форме горки, родившийся в результате какого-то возбуждения (например, удара по воде), который теперь путешествует по бескрайним просторам океана. Это частица. Эта аналогия иллюстрирует главную идею: частицы есть элементарные возбуждения полей. Таким образом, наша реальность — полевая, а мы состоим лишь из элементарных возбуждений этих полей. Будучи рожденными этими самыми полями, их кванты содержат в себе все свойства своих прародителей. Такова роль частиц в мире, в котором одновременно существует множество океанов, именуемых полями. С классической точки зрения поля сами по себе — это обычные числовые функции. Они могут состоять только из одной функции (скалярные поля), а могут — из множества (векторные, тензорные и спинорные поля).
Действие
Вот теперь пришло время снова вспомнить о том, что каждая траектория, по которой физическая система переходит из состояния-1 в состояние-2, формируется некоторой амплитудой вероятности. В своих работах американский физик Ричард Фейнман предположил, что вклады всех траекторий равны по величине, но отличаются на фазу. По-простому, если у вас волна (в данном случае — квантовая волна вероятности) путешествует из одной точки в другую, фаза (деленная на множитель 2π) показывает, сколько колебаний укладывается на этом пути. Эта фаза есть число, которое вычисляется с помощью некоторого правила. А число это называется действием.
В основе мироздания, по сути, лежит понятие красоты, которое получило отражение в термине «симметрия»
Остается осадок оттого, что не очень понятно, что это за число такое — действие? Если сильно не приглядываться, то это некоторая абстрактная математическая величина, которая, на первый взгляд, не имеет никакого отношения к физике — кроме того, что она случайным образом выплевывает известный нам результат. На самом деле все намного интереснее. Принцип наименьшего действия в самом начале был получен как следствие законов Ньютона. Потом на его основе сформулировали законы распространения света. Также его можно получить из уравнений, описывающих законы электричества и магнетизма, а потом в обратную сторону — из принципа наименьшего действия прийти к этим же законам.
Атом азота © iStock
Замечательно, что разные, на первый взгляд, теории обретают одинаковую математическую формулировку. И это наталкивает нас на следующее предположение: не можем ли мы сами придумывать какие-нибудь законы природы с помощью принципа наименьшего действия, а потом искать их в эксперименте? Можем и делаем! В этом и состоит значение этого неестественного и сложного для понимания принципа. Но он работает, что заставляет задуматься о нем именно как о некоторой физической характеристике системы, а не как об абстрактной математической формулировке современной теоретической науки. Важно также отметить, что мы не можем писать любые действия, которые подскажет нам наше воображение. Пытаясь придумать, как должно выглядеть действие очередной физической теории поля, мы используем симметрии, которыми обладает физическая природа, и наряду с фундаментальными свойствами пространства-времени мы можем использовать множество других интересных симметрий, которые подсказывает нам теория групп (раздел общей алгебры, изучающий алгебраические структуры, называемые группами, и их свойства. — Прим. ред.).
О красоте симметрии
Замечательно, что мы получили не просто сводку законов, описывающую какие-то природные явления, а именно способ теоретически получать законы типа ньютоновских или уравнений Максвелла. И хотя квантовая теория поля описывает элементарные частицы лишь на уровне низких энергий, она уже сослужила хорошую службу физикам во всем мире и пока является единственной теорией, здраво описывающей свойства самых мелких кирпичиков, составляющих наш мир. То, чего, собственно, хотят ученые, — это написать такое вот действие, только квантовое, которое содержало бы в себе сразу все возможные законы природы. Хотя даже если бы это удалось, то не разрешило бы всех интересных нам вопросов.
В основе глубинного понимания законов природы лежат некоторые сущности, которые имеют чисто математическую природу. И сейчас, чтобы попытаться проникнуть в глубины мироздания, приходится отказываться от качественных, интуитивно понятных аргументов. Рассказывая о квантовой механике и квантовой теории поля, очень тяжело найти понятные и наглядные аналогии, но самое главное, что я хотел бы донести, — это то, что в основе мироздания лежит, по сути, понятие красоты, которое получило отражение в термине «симметрия». Симметрия поневоле ассоциируется с красотой, как это было, например, у древних греков. И именно симметрии наряду с законами квантовой механики лежат в основе устройства самых маленьких кирпичиков мира, до которых к настоящему моменту удалось добраться физикам.
Квантовое поле, другие измерения.
В последние годы среди мистически настроенных мошенников и честных, но малообразованных людей, всё нарастающую популярность приобретают наукообразные термины. Такие как переход в другое измерение, информационно-волновые технологии, полевые структуры, всевозможные поля – информационные, торсионные и прочие.
Новейшее веяние – квантовое поле. Пишут о нём неумные малограмотные люди, у которых каша в голове. Они не имеют ни малейшего понятия о квантовой теории поля, но при этом пишут о квантовом поле. Пишут всякую ахинею. Ведь они даже о классических полях ничего толком не знают, не говоря уже о квантованных полях.
Приведу несколько примеров этого идиотизма.
Маразм 1. «Душа – летописец, который ведёт список завершенных и незавершенных дел каждого человека в Божественном разуме, этой вездесущей субстанции, которую древние называли «хрониками Акаши» и которая на самом деле есть пространство. Сегодня вместо этого термина мы используем гораздо более сложный – квантовое поле. Это духовное наименование Божественного разума».
Из соображений «политкорректности» ссылку не дам, но любознательный читатель с помощью Google или другой системы поиска найдёт все интересующие его ссылки самостоятельно.
А неучи физики даже не подозревали, что квантовая теория поля имеет дело с божественным разумом!
Маразм 2. «То, что называется «потоком ци» (а физики, возможно, называли бы «универсальным потоком энергии» или «квантовым полем»), не имеет ни начала, ни конца».
Ещё один сюрприз для физиков! Оказывается, квантовая теория поля изучает ци!
Маразм 3. «Квантовое поле — это просто другое название поля чистого сознания и чистой потенциальности».
Маразм крепчал. Оказывается, квантовая теория поля изучает не только ци, но и чистое сознание, а также и чистую потенциальность! Господа маразматики, вы знаете, что такое потенциальность? А что такое чистая потенциальность? Чем она отличается от грязной потенциальности?
Маразм 4. «Система человека тело/разум – выражение того же квантового поля»
Эта авторша, не имеющая никакого понятия о квантовании поля, договорилась до связи квантованного поля – математического объекта – с придуманной ею системой тело/разум! Да ещё наплела чепухи о принципе неопределённости, о котором у неё тоже нет ни малейшего понятия. Вероятно, она даже не знает, кто такой Вернер Гейзенберг, чьим именем назван принцип неопределённости.
Квантование поля – это математическая операция, поэтому она никак не затрагивает реальное поле. Квантованное поле – это математический, а не реальный объект. Сейчас вместо слов «квантованное поле» иногда говорят «квантовое поле», но суть от этого не меняется. Это всего лишь абстракция, математический способ описания реального поля.
И вот некие придурки заявляют, что этот математический объект, оказывается, является Божественным разумом, полем чистого сознания и чистой потенциальности. Сами они понимают, что говорят?
Раньше мне было смешно читать упомянутую выше белиберду, а теперь становится не до смеха, поскольку эта зараза разрослась настолько, что употреблять маразматические словечки начали даже некоторые уважаемые мною люди с гуманитарным образованием. Обычно они делают это в связи с экстрасенсорными способностями и прочими чудесами. «Попала в другое измерение», – пишет иная писательница, не понимая, что это выражение глупо.
Вот и появилось у меня желание хотя бы немного просветить таких уважаемых людей в предельно понятной форме.
Многомерные пространства заинтересовали физиков приблизительно в начале двадцатого века. Например, в памятном нам 1917 году известный физик Пауль Эренфест выпустил статью, в которой обратил внимание на тот факт, что в четырехмерном пространстве орбиты планет неустойчивы. Я говорю только о пространственных измерениях, а не о времени.
Даже если бы планеты каким-то чудом образовались вокруг звезды в четырехмерном пространстве, они быстро упали бы не неё.
Кстати недавно математические физики Соединённого Королевства доказали, что в пространстве размерности пять и более черные дыры тоже нестабильны.
Наше пространство трёхмерное! И никаких других измерений больше нет, кроме свёрнутых, о которых речь пойдёт ниже.
Через пару лет Теодор Калуца попытался объединить в единой теории электромагнитные и гравитационные силы. Для этого он ввёл пятое измерение в дополнение к трём пространственным и одному временному измерению. Это пятое измерение было чисто формальным, без всякого физического смысла. Но впоследствии это пятое измерение пытались интерпретировать как «свёрнутое» или «свернувшееся».
В наше время теоретики ломают мозги над суперструнами, в которых много свёрнутых измерений. Свёрнутые измерения могут существовать лишь в ничтожно малых объёмах, в которых жизнь невозможна. Там не поместятся даже вирусы.
Все эти теории имеют сложный математический аппарат, разобраться в котором не каждый способен.
Кстати, математики – это такие странные люди, которые порой измышляют чудовищные вещи.
Например, вы можете представить себе пространство, в котором расстояние от точки А до точки Б не равно обратному расстоянию от точки Б до точки А? Такое хитрое пространство может выдумать только математик.
Эти чудики уже навыдумывали столько всякой несуразицы, что сам чёрт мозги сломит.
Конечно, современная физика не может объяснить некоторые чудеса. Не помогает даже мудрёная математика.
Поэтому простор для фантазии у писателей и мошенников остаётся огромный. Но нельзя же дурить малограмотных людей терминами, смысла которых сам не понимаешь.
Душу надо называть душой, а не информационной матрицей, полевой структурой или другими псевдонаучными кличками. Употребляйте не наукообразные, а нормальные термины – «тонкий мир», «потусторонний мир», «мир духов», «тот свет».
С чисто математической точки зрения параллельные пространства могут существовать, причём размерность их может быть любой. Если пространства одномерные, то это параллельные прямые. Если пространства двумерные, то это параллельные плоскости. Но жизнь ни в линии, ни в плоскости невозможна.
Параллельные пространства могут быть четырёхмерными, пятимерными и так далее. Но жизнь в таких пространствах тоже невозможна, как показывают несложные физические расчёты.
Остаётся только один вариант – трёхмерные пространства. Теоретически возможен переход из одного трёхмерного мира (пространства) в другой мир, тоже трёхмерный.
Теперь о «переходе в другое измерение».
Предположим, в нашем трёхмерном пространстве есть плоскость, в которой живут странные существа плоскатики.
Если плоскатик выйдет из своей плоскости, означает ли это, что он вышел в другое измерение? Он как был в нашем трёхмерном пространстве, так и остался.
По аналогии можно сказать, что если кроме наших трёх измерений существуют другие измерения, то мы находимся в этом многомерном пространстве, хотя ограничены рамками своего трёхмерного пространства.
Если даже существует четвёртое пространственное измерение, то находящиеся в таком четырёхмерном мире трёхмерные миры должны быть изолированы друг от друга, поскольку, как уже говорилось выше, жизнь в четырёхмерном мире невозможна.
Подобные миры называются бранами в М-теории.
Брана – это объект меньшей размерности, чем размерность пространства, в котором он находится.
Но М-теория создана для описания микромира. А параллельные миры могут существовать и в макромире. Например, наша Вселенная может иметь четыре пространственных измерения или больше, но находящиеся в ней миры должны быть трёхмерными, иначе в них не будет никакой жизни.
Вероятно, иногда происходят переходы из одного трёхмерного параллельного мира в другой. Тогда происходят те самые чудеса, которые невозможно объяснить другим способом.
Люди и вещи пропадают, а из параллельного мира к нам являются неведомые нам люди или знакомые, которые попали в параллельный мир несколько часов или лет назад, а потом случайно вернулись.