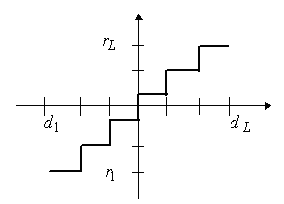что такое квантование изображений
Глубина и квантование цвета
Глубина цвета
Цвет каждого пиксела цифрового изображения описывается несколькими числами (в зависимости от используемой цветовой системы). Количество бит, отводимое на представление информации о цвете каждого пиксела, называют глубиной цвета (color depth) или битовой глубиной цвета (bit depth). Иногда под цветовой глубиной понимают максимальное количество цветов, которые можно представить.
Глубина цвета определяет, как много цветов может быть использовано при отображении одного пиксела. Например, если цветовая глубина равна 1 бит, то пиксел может представлять только один из двух возможных цветов – белый или черный. Если цветовая глубина равна 8 бит, то количество возможных цветов равно 2 8 = 256. При глубине цвета 24 бит количество цветов превышает 16 миллионов, что фактически превосходит способность глаза человека разрешать цвета. Такой режим называется True Color (истинный цвет). В связи с тем, что 24-pазpядное представление неудобно с точки зpения обpаботки изобpажения, обычно в режиме TrueColor используется 32 бита. В случае 32-pазpядного пpедставление информации о цвете младшие тpи байта описывают цвет точки, а стаpший байт либо упpавляет дополнительными паpаметpами (напpимеp, альфа-каналом, инфоpмацией о взаимном пеpекpывании объектов или глубине в тpехмеpном изобpажении), либо не используется. Понятно, что при таком представлении увеличивается размер изображения, однако существенно возрастает скорость его обработки центральным и графическим процессорами компьютера.
Квантование цвета
Квантование цвета (color quantization) используется для получения малого числа характерных цветов в изображении. Задачу квантования в данном случае можно сформулировать как выбор заданного количества «наилучших» цветов, имеющихся в полноцветном изображении, и замены всех остальных цветов изображения подходящими заместителями из этого списка. Раньше процесс квантования цвета был необходим потому, что видеосистема компьютера могла работать лишь с ограниченной цветовой палитрой (как правило, 256 цветов). Теперь оно используется с целью уменьшения размера графического файла, создания спецэффектов, повышения резкости границ и т.п.
Самым простым подходом здесь является выбор комплекта цветов для палитры с равномерным распределением каждой из цветовых компонент. Он обеспечивает широкий выбор цветов, но при этом не учитывается тот факт, что в большинстве изображений нет равномерного цветового распределения.
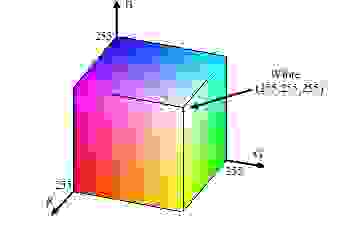
На данный момент существует несколько методик квантования цвета. Одним из наиболее эффективных является метод квантования цветов медианным сечением. При этом цветовое пространство рассматривается как трехмерный куб. Каждая ось куба соответствует одному из трех основных цветов: красному, зеленому или синему. Каждая из трех сторон разбивается на 255 равных частей, деления на осях нумеруются от 0 до 255, причем большее значение соответствует большей интенсивности цвета. Метод медианного сечения делит куб на 256 параллелепипедов, каждый из которых содержит примерно одинаковое количество пикселов. При таком разбиении куба центральная точка каждого параллелепипеда представляет оптимальный выбор для цветовой палитры. В той области куба, которая густо заполнена точками, будет больше параллелепипедов и, соответственно, в палитру попадет больше цветов. А там, где точек меньше, будет взято меньшее количество цветов. При этом ни один цвет не будет отброшен полностью, а предпочтение будет отдано тем цветам, которые встречаются чаще.
Переход от непрерывных сигналов и преобразований к дискретным
В систему обработки информации сигналы поступают, как правило, в непрерывном виде. Для компьютерной обработки непрерывных сигналов необходимо, прежде всего, преобразовать их в цифровые. Для этого выполняются операции дискретизации и квантования.
Дискретизация изображений
Дискретизация – это преобразование непрерывного сигнала в последовательность чисел (отсчетов), то есть представление этого сигнала по какому-либо конечномерному базису. Это представление состоит в проектировании сигнала на данный базис.
Наиболее удобным с точки зрения организации обработки и естественным способом дискретизации является представление сигналов в виде выборки их значений (отсчетов) в отдельных, регулярно расположенных точках. Такой способ называют растрированием, а последовательность узлов, в которых берутся отсчеты – растром. Интервал, через который берутся значения непрерывного сигнала называется шагом дискретизации. Обратная шагу величина называется частотой дискретизации,
Существенный вопрос, возникающий в ходе дискретизации: с какой частотой брать отсчеты сигнала для того, чтобы была возможность его обратного восстановления по этим отсчетам? Очевидно, что если брать отсчеты слишком редко, то в них не будет содержаться информация о быстро меняющемся сигнале. Скорость изменения сигнала характеризуется верхней частотой его спектра. Таким образом, минимально допустимая ширина интервала дискретизации связана с наибольшей частотой спектра сигнала (обратно пропорциональна ей).
Для случая равномерной дискретизации справедлива теорема Котельникова, опубликованная в 1933 году в работе “О пропускной способности эфира и проволоки в электросвязи”. Она гласит: если непрерывный сигнал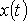 
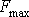
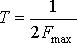
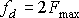
имеет спектр, ограниченный частотой 
, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым с периодом 
, т.е. с частотой 
.
Восстановление сигнала осуществляется при помощи функции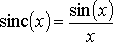 
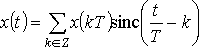
. Котельниковым было доказано, что непрерывный сигнал, удовлетворяющий приведенным выше критериям, может быть представлен в виде ряда:
.
Эта теорема так же еще называется теоремой отсчетов. Функция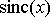 
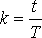
называется еще функцией отсчетов или Котельникова, хотя интерполяционный ряд такого вида изучал еще Уитакер в 1915 году. Функция отсчетов имеет бесконечную протяженность по времени и достигает наибольшего значения, равного единице, в точке 
, относительно которой она симметрична.
Каждую из этих функций можно рассматривать как отклик идеального фильтра низких частот (ФНЧ) на дельта-импульс, пришедший в момент времени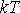 
. Таким образом, для восстановления непрерывного сигнала из его дискретных отсчетов, их необходимо пропустить через соответствующий ФНЧ. Следует заметить, что такой фильтр является некаузальным и физически нереализуемым.
Приведенное соотношение означает возможность точного восстановления сигналов с ограниченным спектром по последовательности их отсчетов. Сигналы с ограниченным спектром – это сигналы, спектр Фурье которых отличен от нуля только в пределах ограниченного участка области определения. Оптические сигналы можно отнести к ним, т.к. спектр Фурье изображений, получаемых в оптических системах, ограничен из-за ограниченности размеров их элементов. Частоту 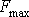называют частотой Найквиста. Это предельная частота, выше которой во входном сигнале не должно быть спектральных компонентов.
Квантование изображений
Рис. 1. Функция, описывающая квантование
Основная задача при этом состоит в определении значений порогов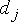 
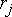
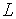
и уровней 
квантования. Простейший способ решения этой задачи состоит в разбиении динамического диапазона на одинаковые интервалы. Однако такое решение не является наилучшим. Если значения интенсивности большинства отсчетов изображения сгруппированы, например, в «темной» области и число уровней 
ограничено, то целесообразно квантовать неравномерно. В «темной» области следует квантовать чаще, а в «светлой» реже. Это позволит уменьшить ошибку квантования.
В системах цифровой обработки изображений стремятся уменьшить число уровней и порогов квантования, так как от их количества зависит объем информации, необходимый для кодирования изображения. Однако при относительно небольшом числе уровней на квантованном изображении возможно появление ложных контуров. Они возникают вследствие скачкообразного изменения яркости проквантованного изображения и особенно заметны на пологих участках ее изменения. Ложные контуры значительно ухудшают визуальное качество изображения, так как зрение человека особенно чувствительно именно к контурам. При равномерном квантовании типичных изображений требуется не менее 64 уровней.
Квантизация изображений
Квантизация — уменьшение цветов изображения (wiki). Конечно, сейчас мало кому это необходимо, но задача сама по себе интересная.
Квантизированная Лена привлекает внимание
Например, старый добрый формат GIF использует палитру, максимум на 256 цветов. Если вы захотите сохранить серию своих селфи как gif-анимацию (кому бы это надо было), то первое, что вам, а точнее программе, которую вы будете для этого использовать, надо будет сделать – создать палитру. Можно использовать статическую палитру, например web-safe colors, алгоритм квантизации получиться очень простым и быстрым, но результат будет «не очень». Можно создать оптимальную палитру на основе цветов изображения, что даст результат наиболее визуально похожий на оригинал.
Алгоритмов создания оптимальной палитры несколько, каждый имеет свои плюсы и минусы. Я не стану утруждать читателя нудной теорией и формулами, во первых мне лень, во вторых большинству это не интересно – статью просто пролистают, рассматривая картинки.
Далее вас ждёт скучное и непонятное повествование о методе медианного сечения, алгоритму рассеивания ошибок (шума квантизации) по Флойду-Стейнбергу (и не только), особенностях цветового восприятия человеческого глаза, а так же немного говнокода.
Итак – метод медианного сечения. Он прост до безобразия. Первым делом надо из всех уникальных цветов изображения составить RGB куб. Далее рассечь его по самой длинной стороне. Например, диапазон красного у нас от 7 до 231 (длина 231-7=224), зелёного от 32 до 170 (длина 170-32=138), синего от 12 до 250 (длина 250-12=238), значит, будем «резать» куб по синей стороне. Получившиеся сегменты так же рассекаем по длинной стороне и т.д. пока не получим 256 сегментов. Для каждого сегмента высчитать средний цвет – так мы и получим палитру.
Что здесь можно улучшить? Первое, что приходит в голову – вычислять средний цвет не тупо сложив все цвета и разделив на их количество [ sum(color) / count(color) ], а с учётом, сколько раз каждый цвет встречается в изображении. То есть каждый цвет умножаем на количество его вхождений в изображении, полученные значения складываем, результат делим на количество вхождений в изображении всех цветов данного сегмента [ sum(color * total) / sum(total) ]. В результате, наиболее часто встречаемые цвета имеют приоритет при вычислении, но и редкие цвета вносят свои корректировки, поэтому палитра получается лучше, визуальное отклонение цветов меньше. Для лучших результатов желательно ещё учитывать гамму, но я оставил это на потом. Второе не так явно – медианное сечение совсем не учитывает особенности восприятия цвета человеческим глазом. Оттенки зелёного мы воспринимаем гораздо лучше оттенков синего. Я решил исправить это недоразумение и «сплющил» куб – длины сторон помножил на коэффициенты из этой статьи. В результате по зелёной и красной стороне сечений стало больше, по синей меньше. Такого решения я больше нигде не встречал (может плохо искал), но результат на лицо.
Теперь у нас есть оптимальная палитра, не идеальная конечно (я знаю, что её можно ещё улучшить), но достаточно хорошая. Следующий шаг – индексирование цветов изображения. Самый простой вариант – в каком сегменте находится цвет, такой и индекс. Быстро и просто. Но есть одно но, и даже не одно, поэтому к данному шагу мы ещё вернёмся.
Есть ещё один способ улучшить качество получаемого изображения – рассеивание ошибок. Тут тоже всё довольно просто – из индексируемого цвета вычитаем соответствующий цвет палитры, получаем ошибку, рассеиваем её по соседним пикселям в соответствии с определённой формулой (шаблоном), самая известная формула Флойда-Стейнберга, её я и использовал. При рассеивании ошибок размываются резкие переходы между цветами, и визуально кажется, что изображение содержит больше оттенков (цветов). Если интересно – про рассеивание ошибок подробно и интересно можно почитать тут. Этот алгоритм я так же решил допилить, помножив ошибку на всё те же коэффициенты, как оказалось, это была очень хорошая идея – так как сечений по синему диапазону стало меньше, в нём получалась значительная ошибка, и без корректировки ошибки коэффициентами рассеивание вносило много «шума».
Вот теперь можно снова вернуться к индексированию. Рассеиванием ошибок мы изменяем цвета пикселей и получаем такие, которых нет в нашем RGB-кубе (напомню, он составлен исключительно из цветов изображения). Теперь нельзя просто посмотреть в каком сегменте находится цвет, чтобы назначить индекс. Решение нашлось сразу – поиск ближайшего цвета в палитре. В данную формулу я подставил всё те же коэффициенты. Сравнивая результаты подбора цвета палитры по индексу сегмента в который входит исходный цвет и результаты поиска ближайшего цвета, наглядно увидел, что ближайший цвет часто оказывается в соседнем сегменте. Если исходный цвет находится ближе к центру сегмента – то индекс сегмента соответствует индексу цвета в палитре, но чем ближе исходный цвет к краям сегмента, тем больше вероятность, что ближайший цвет окажется в соседнем сегменте. В общем, единственный правильный путь индексирования – поиск ближайшего цвета в палитре. Но у поиска есть минус – он медленный, очень медленный. Писать числодробилку на python плохая идея.
Ну вот, хотел объяснить в двух словах, а получилась целая куча непонятной писанины. Надеюсь, код я пишу лучше, чем объясняю, поэтому вот ссылочка на github. Код несколько раз переписывался, сначала совершенствовался алгоритм, пока результат меня не устроил, потом оказалось, что он жрёт слишком много оперативы при обработке фотографий (сначала тестировал на небольших картинках), пришлось перенести RGB-куб, медианное сечение и карту пикселей в базу данных (sqlite). Скрипт работает очень медленно, но результат получается лучше, чем квантизация средствами PIL/Pillow и GIMP’ом (в нём эта операция называется индексирование).
Оригинал 
Результат квантизации в GIMP, оптимальная палитра на 256 цветов + размывание цвета по Флойду-Стенбергу (нормальное)
Результат квантизации PIL/Pillow
Результат квантизации моим кодом
На что обратить внимание: рассеивание ошибки у GIMP сильно «шумит», PIL/Pillow создает не очень оптимальную палитру и практически не рассеивает ошибки (резкие переходы между цветами).
Если не видите разницу — посмотрите другие примеры на github.
СОДЕРЖАНИЕ
Алгоритмы
Был изобретен ряд других, гораздо менее часто используемых методов, в которых используются совершенно другие подходы. Алгоритм Local K-means, разработанный Олегом Веревкой в 1995 году, предназначен для использования в оконных системах, где основной набор «зарезервированных цветов» фиксирован для использования системой, и многие изображения с разными цветовыми схемами могут отображаться одновременно. Это схема пост-кластеризации, которая делает первоначальное предположение о палитре, а затем итеративно ее уточняет.
В первые дни цветового квантования алгоритм кластеризации k-средних считался непригодным из-за его высоких вычислительных требований и чувствительности к инициализации. В 2011 году М. Эмре Челеби повторно исследовал эффективность k-средних в качестве квантователя цвета. Он продемонстрировал, что эффективная реализация k-средних превосходит большое количество методов квантования цвета.
История и приложения
На заре ПК видеоадаптеры обычно поддерживали только 2, 4, 16 или (в конечном итоге) 256 цветов из-за ограничений видеопамяти; они предпочли посвятить видеопамять большему количеству пикселей (более высокое разрешение), чем большему количеству цветов. Цветовое квантование помогло оправдать этот компромисс, сделав возможным отображать множество изображений с высоким содержанием цветов в 16- и 256-цветных режимах с ограниченным визуальным ухудшением качества изображения. Многие операционные системы автоматически выполняют квантование и дизеринг при просмотре цветных изображений в 256-цветном видеорежиме, что было важно, когда доминировали видеоустройства, ограниченные 256-цветными режимами. Современные компьютеры теперь могут отображать миллионы цветов одновременно, гораздо больше, чем может различить человеческий глаз, ограничивая это приложение в первую очередь мобильными устройствами и устаревшим оборудованием.
Из-за того, что на ранних компьютерах было доступно немного цветов, разные алгоритмы квантования давали очень разные изображения на выходе. В результате много времени было потрачено на написание сложных алгоритмов, чтобы они были более реалистичными.
Поддержка редактора
Многие редакторы растровой графики содержат встроенную поддержку квантования цветов и автоматически выполняют это при преобразовании изображения с большим количеством цветов в формат изображения с меньшим количеством цветов. Большинство из этих реализаций позволяют пользователю точно установить количество желаемых цветов. Примеры такой поддержки включают:
Алгоритмы квантования для полутоновых и цветных изображений
12.4. Алгоритм медианного сечения
Первый шаг алгоритма заключается в нахождении минимального параллелепипеда, так что все значения атрибутов пикселей исходного изображения принадлежат ему. Далее происходит процедура разбиения параллелепипеда.
Предыдущая процедура повторяется для каждого из параллелепипедов до тех пор, пока не сформируется N параллелепипедов, где N равно желаемому размеру палитры.
Следующий шаг выполняется после формирования N параллелепипедов и призван заполнить палитру. Палитра заполняется либо центральными точками параллелепипедов, либо средними арифметическими значений, попавших в данные параллелепипеды.
Далее проводится процедура нахождения соответствующего параллелепипеда для данного значения атрибута исходного изображения и замены значения на новое.
Часто реализации алгоритма используют специальные структуры для хранения разбиения цветового пространства. Примером такой структуры может служить BSP дерево (подробнее см. [23]).
Результаты работы алгоритма являются очень хорошими (см. рис. 12.4); при этом скорость работы данного алгоритма высока. Различные вариации данного алгоритма используются в известных приложениях для обработки изображений, например в GNU ImageManipulation Program (GIMP).
12.5. Методы кластеризации для квантования изображений
Метод K-средних
Выберем случайным образом K значений атрибутов из исходного изображения и положим их центрами кластеров. Сгруппируем точки по кластерам, т.е. отнесем значение к кластеру, центр которого находится ближе всего к значению. Далее для каждого кластера пересчитаем его центр (т.е. среднее арифметическое всех значений, входящих в кластер). Последнюю операцию нужно повторять до тех пор, пока либо перемещения значений из одного кластера в другой не прекратятся, либо после определенной (заданной наперед) итерации отношение перемещенных значений ко всем станет меньше, чем заданное наперед значение. Таким образом, будет сформировано K кластеров, соответствующих палитре. Палитру следует заполнить центрами кластеров. Заметим, что одновременно нам становится известна вся информация о квантовании, т.е. не только палитра, но и индивидуальная принадлежность значений атрибутов исходного изображения к конкретному кластеру (см. алгоритм 12.5).
Недостатком данного метода является то, что он способен эффективно выделять лишь те кластеры, которые по форме близки к сферическим. Достоинством данного метода является высокая скорость работы. Применительно к квантованию изображений данный метод показывает очень хорошие результаты (см. рис. 12.5).