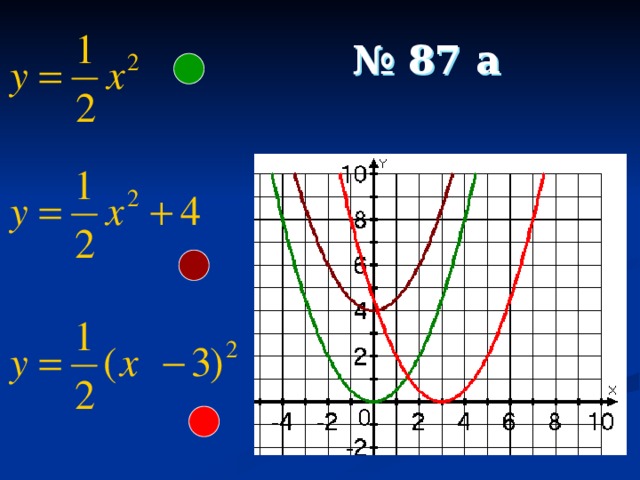
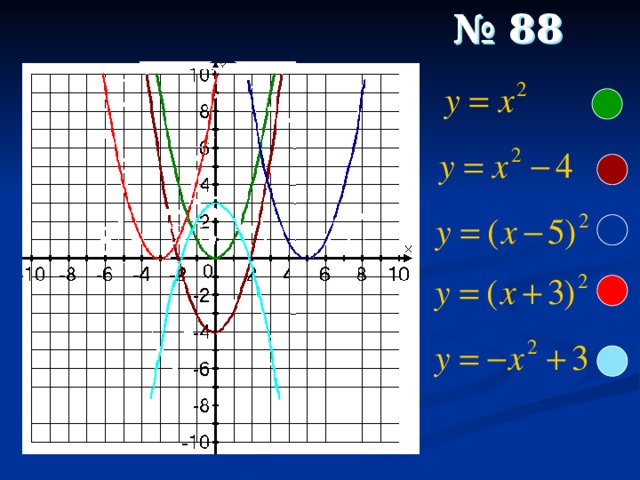
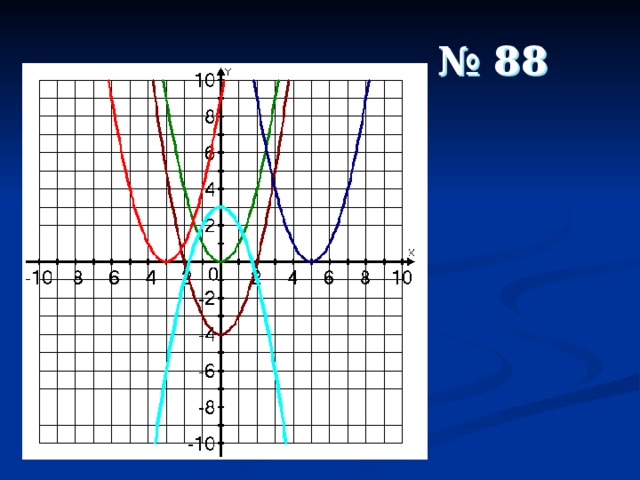
что такое квадратичная функция в алгебре 9 класс
Урок алгебры в 9-м классе «Квадратичная функция. Ее свойства и график»
Разделы: Математика
Цели – обобщить и систематизировать знания учащихся о квадратичной функции: повторить изученные приемы исследования свойств функции, методы построения графиков; закрепить и упрочить умения и навыки учащихся по данной теме, показать ее прикладной характер, ориентировать на использование полученных знаний при дальнейшем изучении математики.
План урока:
Ход урока
Учитель: Ребята, сегодня мы с вами продолжаем вести разговор об одном из важных разделов математики – функциональной зависимости. Прежде всего вспомним определение функции.
Ученик: Функция – это такая зависимость переменной у от переменной х, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Учитель: Какую функцию называют квадратичной? Что является ее графиком?
Ученик: Квадратичной функцией называется функция. которую можнозадать формулой вида y = ax 2 + bx + c, где x – независимая переменная, a, b и с – некоторые числа, причем а 
Учитель: С какими способами построения графиков квадратичной функции мы познакомились?
Ученик:
Учитель: Повторим некоторые этапы построения графиков квадратичной функции при выполнении теста – разминки.
I. Разминка (ученики устно отвечают на вопросы теста, подготовленного на карточки или слайды). В это время предложить трем ученикам самостоятельно решить на доске задачи.
Тест:
Ответы: 1b; 2c; 3b; 4a; 5b.
Индивидуальные задания на доске:
1. Параболу у = 2х 2 сдвинули влево на 3 единицы и вниз на 5 единиц. Задайте формулой функцию, график которой получился в результате таких преобразований.
Решение: у = 2(х + 3) 2 – 5.
2. Найдите область значений функции у = х 2 – 2х.
Решение:Функция ограничена снизу, у0 =


3. Постройте график функции у = (3 – x)(х+ 1).

II. Фронтальная работа.
Задание классу (ученик у доски):
По графику проведите исследование свойств функции.
Индивидуальные задания на карточках:
1. Определите, при каких значениях с наименьшее значение функции у = 2х 2 + 16х + с равно 2.
Решение:



2. Определите, при каких значениях b и c вершиной параболы у = х 2 + bx + c является точка А(–2; –1).
Решение: 





III. Работа в группах.
Задание группам:
Решение:
Дополнительно: Построить график функции у = 3х 2 + 6|х| + 6.
Индивидуальные задания на карточках (ученики выполняют на доске, объясняют решение классу после работы по группам):
Решение: х0 = 1 
2. Найти наименьшее значение функции у = 2(х +3) 2 на отрезке [– 4; 1]
3. По графику у = ах 2 + bx + c определите знаки чисел a, b, c. (рисунок 4)
Решение:
IV. Решение задачи с практическим содержанием на применение свойств квадратичной функции. (Ученик у доски)
Требуется оградить прямоугольную площадку, примыкающую к стене. Забор должен иметь длину 60 м. Какой должна быть длина и ширина площадки, чтобы площадь ее была бы наибольшей?
Решение:
При х = 15 унаиб = 450. Ширина – 15 м, длина – 30 м.
V. Тест.
Вариант I
Вариант II
VI. Итоги урока.
VII. Домашнее задание.
Домашняя контрольная работа
Вариант I
Вариант II
Квадратичная функция, ее свойства и график (алгебра, 9 класс)
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
1. Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось симметрии. 2. Определить направление ветвей параболы. 3. Найти координаты еще нескольких точек, принадлежащих искомому графику ( в частности, координаты точки пересечения параболы с осью у и нули функции, если они существуют). 4. Отметить на координатной плоскости найденные точки и соединить их плавной линией. График любой квадратичной функции – парабола.
Выделим квадрат двучлена из квадратного трехчлена ах2 + bх + с ах2 + bx + с = а (х2 + x ) + с = = а + с = = а + с = а
Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение b2 – 4ac Его обозначают буквой D, т.е. D= b2 – 4ac. Возможны три случая: D 0 D 0 D 0
если дискриминант больше нуля, то парабола пересекает ось абсцисс в двух точках, если дискриминант равен нулю, то парабола касается оси абсцисс, если дискриминант меньше нуля, то парабола не пересекает ось абсцисс, абсцисса вершины параболы равна
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-1239033
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Приамурье начнут пускать на занятия только привитых студентов
Время чтения: 0 минут
В Москве запустили онлайн-проект по борьбе со школьным буллингом
Время чтения: 2 минуты
Систему ЕГЭ сделают независимой от Microsoft
Время чтения: 1 минута
Путин попросил привлекать родителей к капремонту школ на всех этапах
Время чтения: 1 минута
Минобрнауки разработало концепцию преподавания истории российского казачества
Время чтения: 1 минута
В Воронежской области ввели масочный режим в школах
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Квадратичная функция, её график и свойства
Описание разработки
Презентация содержит 32 слайда.
Квадратичной функцией называется функция, которую можно задать формулой вида y = ax 2 + bx + c, где x – независимая переменная, a, b и c – некоторые числа, причем a не равно 0.
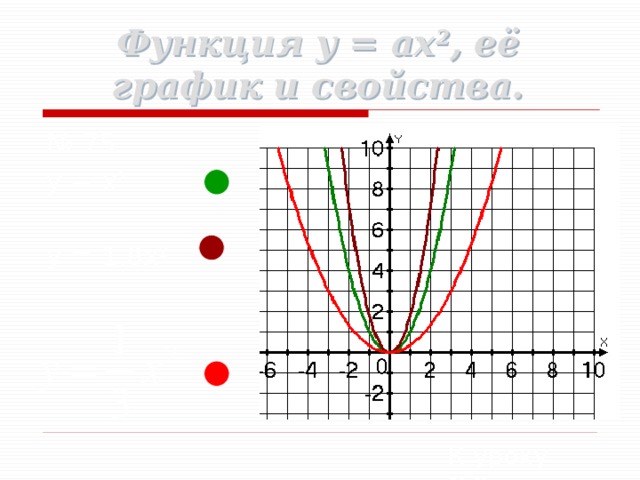
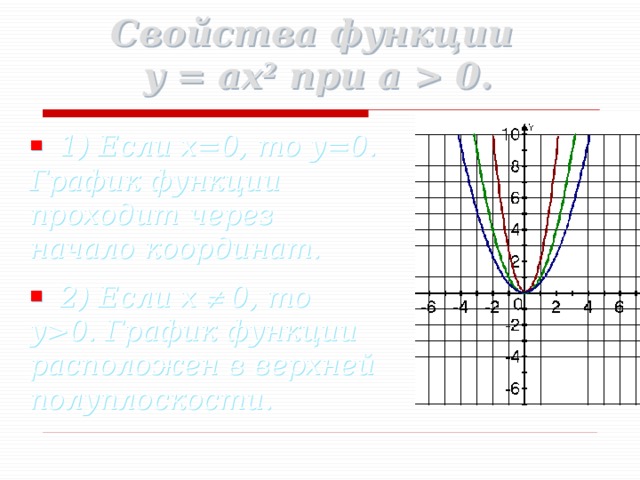
Свойства функции y = ax 2 при a > 0.
1) Если x=0, то y=0. График функции проходит через начало координат.
2) Если x не равен 0, то y>0. График функции расположен в верхней полуплоскости.
3) Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y.
4) Функция убывает в промежутке (- бесконечности;0] и возрастает в промежутке [0;+бесконечности).
5) Наименьшее значение равное нулю, функция принимает при x=0, наибольшего значения функция не имеет. Областью значений функции является промежуток [0;+бесконечность).
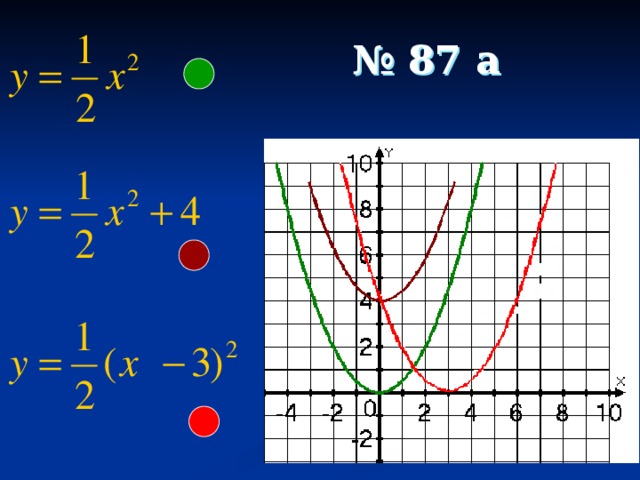
Свойства функции y = ax 2 при a 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n > 0, или на –n единиц вниз, если n 2 является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m > 0, или на –m единиц влево, если m 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m > 0, или на –m единиц влево, если m 0, или на –n единиц вниз, если n
Квадратичной функцией называется функция, которую можно задать формулой вида
где x – независимая переменная, a, b и c – некоторые числа, причем a 0.
Частный случай квадратичной функции
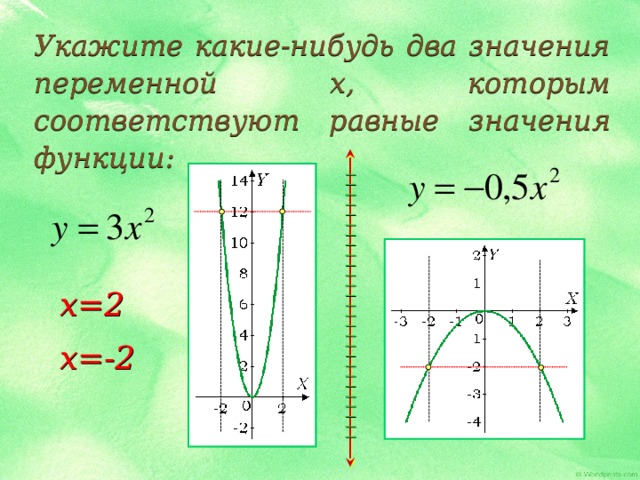
Укажите какие-нибудь два значения переменной x, которым соответствуют равные значения функции:
Не выполняя вычислений, сравните значения выражений:
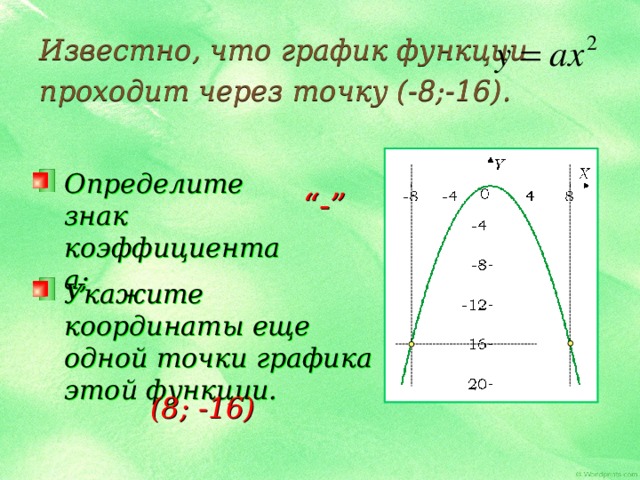
Известно, что график функции проходит через точку (-8;-16).
Определите знак коэффициента а;
Укажите координаты еще одной точки графика этой функции.
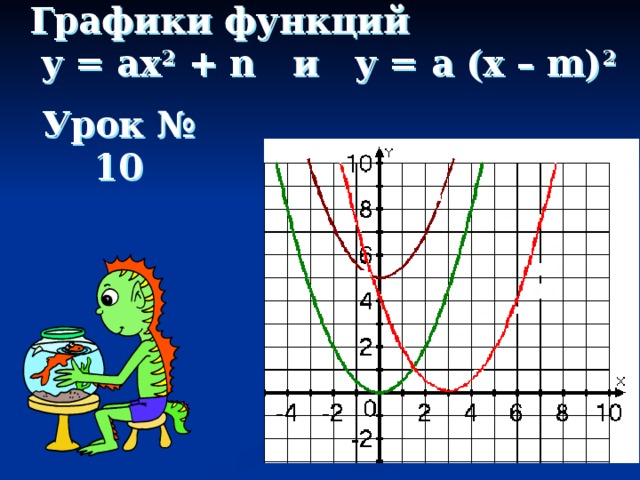
Графики функций y = ax 2 + n и y = a (x – m) 2

Графики функций y = ax 2 + n и y = a (x – m) 2
График функции y = ax 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n 0, или на –n единиц вниз, если n

Графики функций y = ax 2 + n и y = a (x – m) 2
График функции y = a (x – m) 2 является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m 0, или на –m единиц влево, если m

График функции y = a (x – m) 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m 0, или на –m единиц влево, если m 0, или на –n единиц вниз, если n
Производить параллельные переносы можно в любом порядке.
График функции y = f (x – m) + n можно получить из графика y = f (x) с помощью двух соответствующих параллельных переносов.
Построение графика квадратичной функции.
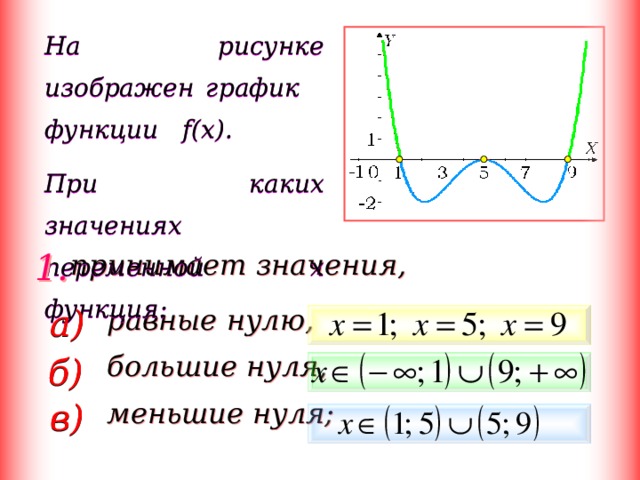
На рисунке изображен график функции f(x).
При каких значениях переменной x функция:
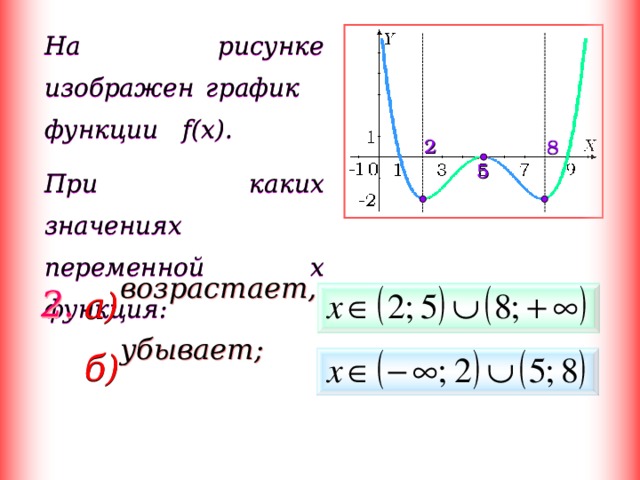
На рисунке изображен график функции f(x).
При каких значениях переменной x функция:
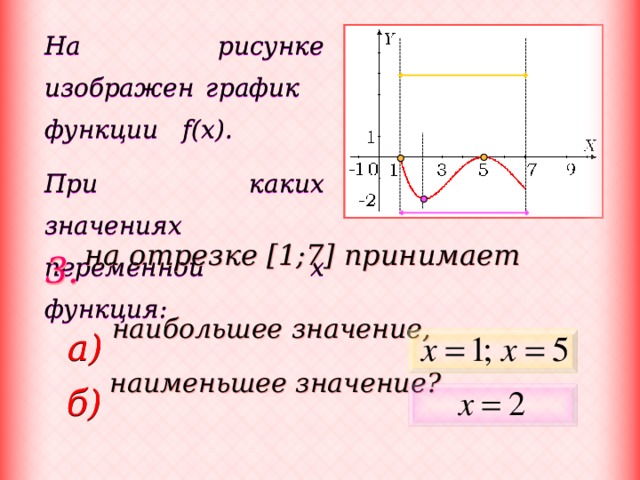
На рисунке изображен график функции f(x).
При каких значениях переменной x функция:
Квадратичная функция. Парабола
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Квадратичная функция — это функция вида
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит « x » — это « 2 », то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты « a », « b » и « с ».
Как построить график квадратичной функции
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции « y = x 2 −7x + 10 ».
Если « a > 0 », то ветви направлены вверх.
Если « a », то ветви направлены вниз.
В нашей функции « a = 1 », это означает, что ветви параболы направлены вверх.
Чтобы найти « x0 » (координата вершины по оси « Ox ») нужно использовать формулу:
Найдем « x0 » для нашей функции « y = x 2 −7x + 10 ».
Теперь нам нужно найти « y0 » (координату вершины по оси « Oy »). Для этого нужно подставить найденное значение « x0 » в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси « Oy ».
Для начала давайте разберемся, что называют нулями функции.
Нули функции — это точки пересечения графика функции с осью « Ox » (осью абсцисс).
Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси « Oy » равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y = 0 ».
0 = x 2 −7x + 10
x 2 −7x + 10 = 0
x1;2 =
| 7 ± √ 49 − 4 · 1 · 10 |
| 2 · 1 |
x1;2 =
| 7 ± √ 9 |
| 2 |
x1;2 =
| 7 ± 3 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 5 | x2 = 2 |
Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью « Ox ». Назовем эти точки и выпишем их координаты.
Отметим полученные точки («нули функции») на системе координат.
Возьмем четыре произвольные числовые значения для « x ». Целесообразно брать целые числовые значения на оси « Ox », которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.
Для каждого выбранного значения « x » рассчитаем « y ».
Запишем полученные результаты в таблицу.
| x | 1 | 3 | 4 | 6 |
| y | 4 | −2 | −2 | 4 |
Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции « y = −3x 2 − 6x − 4 ».
x0 =
| −b |
| 2a |
x0 =
| −(−6) |
| 2 · (−3) |
=
| 6 |
| −6 |
= −1
y0(−1) = (−3) · (−1) 2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
Точки пересечения с осью « Ox » ( y = 0 ).
x1;2 =
| −6 ± √ 6 2 − 4 · 3 · 4 |
| 2 · 1 |
x1;2 =
| −6 ± √ 36 − 48 |
| 2 |
x1;2 =
| −6 ± √ −12 |
| 2 |
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось « Ox ».
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки « (−2; −4) » и « (0; −4) ». Построим и подпишем график функции.